7.3. Differentiable Functions
Again we take the result of 7.1. as our guideline. We have already transferred the spectrum of secant gradients into a mathematical notion,
so the remaining task will be to deal with the tangent gradient. We take [7.1.2] as a pattern.
|
Definition: Let
be an accumulation point of .
We call a function differentiable at a, if the difference quotient function
is continuously extendable at a. In this case the real number (read: f-prime at a)
|
[7.3.1] |
is called derivative (more precise: derivative number) of f at a.
|
Consider:
Being the limit of secant gradients we regard
as
the gradient of the tangent at f in (a, f(a)). As a is a accumulation point of A - and thus also of
- has at most one continuous extension at a. Therefor the limit at a, i.e. the
number is uniquely determined.
The symbol is due to Cauchy. Although quite common it is not seldom replaced by Leibniz's notation and respectively. The idea behind is, that when "performing the limit process" the quotient of the differences and will switch over into the
mystic
i  |
|
Note that there was no precise limit idea for Leibniz (1646 - 1716) and it was not until Cauchy (1789 - 1857) who developed a modern, satisfactory concept.
|
quotient of differentials df and dx. We read as "dee eff dee ecks" to indicate, at least when reading, that there is no real quotient. -
Again physics has its own notation at this point: With time related functions, e.g. with those of the type (cf. the note in [7.2]) the derivative number is denoted by a dot symbol
and referred to as the instantaneous speed at the time . It is usually replaced by .
It is this textual concept that the alternative term "instantaneous rate of change of the function f at a" for the derivative comes from.
Example:
-
Every linear function is differentiable at each
with
►
| [7.3.2] |
Proof: According [7.2.2] is continuously extendable at a by the constant function m on .
Thus we have:
.
-
With the power function is differentiable at every and
►
| [7.3.3]
|
Proof: From [7.2.3] we see that is continuously extendable at a by . From this we calculate the derivative number:
.
-
The reciprocal function is differentiable at every with
►
| [7.3.4] |
Proof: According [7.2.4]
is the continuous extension of at a. So we get the following derivative number
.
-
The root function is differentiable at every
and
►
|
[7.3.5] |
Proof: [7.2.5] shows that is continuously extended at a by ,
yielding
as derivative number.
-
The root function is not differentiable at 0. The difference quotient function is not continuously extendable at 0. We see this from ,
a sequence in converging to 0, with the image sequence
being divergent.
-
The absolute value function is not differentiable at 0:
(cf. [7.2.6]) can't be continuously extended.
Take e.g. the zero sequence
in . The image sequence
is divergent.
|
Consider:
We started our issue looking for tangents. Having set up the derivative numbers the main problem, getting the correct gradient, is now solved. So we are prepared to build tangents.
Definition:
Let be differentiable at .
We call the function
|
[7.3.7] |
the tangent function of f with respect to a.
|
Consider:
Occasionally we write instead of to point to the relation to f.
is a linear function, touching the graph of f in (a, f(a)). Note that , and that
is the gradient factor of .
Independently from A tangent functions always have the whole of as their domain.
Working with tangents often comprises the search for the so called normal of f, i.e. the perpendicular to the tangent running through (a, f(a)). There is a linear function to represent non-vertical normals:
|
Definition: If is differentiable at such that the function
|
[7.3.8] |
is called the normal function of f with respect to a.
|
Consider:
If necessary we use the more detailed notation for the normal function. As and f actually intersect at a. Its slope is the reciprocal of the slope of with a reversed sign. is thus
perpendicular
i  |
|
Rotating a straight line g with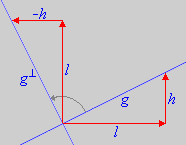 non-zero slope by 90° results in a perpendicular line with a slope of non-zero slope by 90° results in a perpendicular line with a slope of
|
to . Independently from A normal functions always have the whole of as their domain.
As an example we calculate the tangent and normal function for the cubic function with respect to 1. With and we have
|
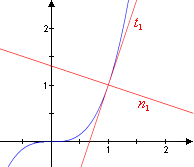 |
Exercise: Calculate the tangent and normal function of
with respect to 4:
-
with respect to −1:
-
with respect to a:
|
It is an advantage to switch to the vector notation and represent a tangent as a line. We only need to know one point of that line, (a, f(a)) is the most obvious one, and to calculate a directional vector. Having in mind that for an horizontal increment of 1 the derivative is the appropriate vertical increment we find our vector representation as follows:
|
[7.3.9] |
As both vectors and are perpendicular to each other the normal could be represented as
|
[7.3.10] |
[7.3.10] has the additional advantage that vertical normals are included as well. Consider however that in the non-vertical case and represent the same direction.
For an example we return to . The tangent of with respect to 1 is the line and its normal is .
|
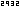 |
|
 non-zero slope by 90° results in a perpendicular line with a slope of
non-zero slope by 90° results in a perpendicular line with a slope of