5.5. Properties of Convergent Sequences

The first question to study will be if convergence has implications on monotony and boundedness. The results however are poor. As we find monotone and non-monotone sequences among the convergent sequences, and among the non-convergent ones as well, there is no connexion between monotony and convergence. A slight improvement is known with boundedness: Though there are divergent bounded sequences, take e.g.

({(- 1)}^{n})

, we can prove that convergence always implies boundedness.

Proposition:

Each convergent sequence is bounded.

[5.5.1]

Proof: If $a_{n} \to g$ , then according to [5.4.2] we find especially for 1 a number $n_{0} \in ℕ^{*}$ , such that

g - 1 < a_{n} < g + 1 for all n \geq n_{0}

From that we get for all $n \in ℕ^{*}$ :

\min {g - 1, a_{1}, \dots, a_{n_{0} - 1}} \leq a_{n} \leq \max {g + 1, a_{1}, \dots, a_{n_{0} - 1}}

One conclusion is a new criterion for divergence:

Unbounded sequences are always divergent.

Thus the divergence of e.g. $(n)$ is also due to its unboundedness.

There are certain connexions between the position of the sequences members and the position of the limit. More precisely we have:

Proposition: Let $a_{n} \to g$ . Then we have for any $c \in ℝ$ :

$g > c \Rightarrow a_{n} > c$ for all n as of an appropriate $n_{0}$

$g < c \Rightarrow a_{n} < c$ for all n as of an appropriate $n_{0}$

[5.5.2]

$a_{n} \geq c for all n \Rightarrow g \geq c$

$a_{n} \leq c for all n \Rightarrow g \leq c$

[5.5.3]

Proof: We only show the first variant in each case.

1. ►
Let $g > c$ , i.e. $r ≔ g - c > 0$ . As $a_{n} \to g$ the special $ε$ -neighbourhood $] g - r, g + r [$ contains all sequence members from a certain $n_{0}$ onwards. In particular this means:
$a_{n} > g - r = g - (g - c) = c for all n \geq n_{0} .$

2. ►
Suppose $g < c$ . According to 1. we may conclude $a_{n} < c$ for nearly all n. But this contradicts the premise $a_{n} \geq c$ for all n.

Consider:

1. is often used, especially if $c = 0$ , the following way:

$g \neq c \Rightarrow a_{n} \neq c$ for all n as of an appropriate $n_{0}$
[5.5.4]

The example $0 < \frac{1}{n} \to 0$ shows that 2. cannot be tightened by replacing e.g. $\geq$ by $>$ .
As $a_{n} \to g \Leftrightarrow a_{n + k} \to g$ we may however in 2. extenuate the premise to 'for nearly all n'.

Obviously both statements in 2. can be combined to:

$a_{n} \in [a, b] for all n \Rightarrow g \in [a, b]$
[5.5.5]

When testing zero sequences for convergence we may confine ourselves to positive sequences, which often provides some technical comfort.

Proposition: For any sequence $(a_{n})$ we have:

a_{n} \to 0 \Leftrightarrow | a_{n} | \to 0

[5.5.6]

Proof: From the equality $| a_{n} - 0 | = | a_{n} | = | | a_{n} | - 0 |$ we see that for each $ε > 0$ the following equivalence holds:

| a_{n} - 0 | < ε \Leftrightarrow | | a_{n} | - 0 | < ε

And from that our assertion is immediate.

Let's take $(\frac{{(- 1)}^{n}}{n})$ as an example. From $| \frac{{(- 1)}^{n}}{n} | = \frac{1}{n} \to 0$ we get:

\frac{{(- 1)}^{n}}{n} \to 0

Approaching the limit of a convergent sequence has implications for the sequence members among themselves: Their distance to each other will also decrease arbitrarily. The following property of a convergent sequence is called the Cauchy-Condition.

Proposition: If $a_{n} \to g$ there is an $n_{0} \in ℕ^{*}$ for each $ε > 0$ such that

| a_{n} - a_{m} | < ε for all n, m \geq n_{0}

[5.5.7]

Proof: At first we get an $n_{0} \in ℕ^{*}$ such that

| a_{n} - g | < \frac{ε}{2} for all n \geq n_{0} .

Thus, using the triangle inequality, the following estimate holds for all $n, m \geq n_{0} :$

| a_{n} - a_{m} | = | a_{n} - g + g - a_{m} | \leq | a_{n} - g | + | a_{m} - g | < \frac{ε}{2} + \frac{ε}{2} = ε

It is interesting to ask if the Cauchy-Condition alone implies convergence. In general the answer is 'No'. There is a divergent sequence in $ℚ$ satisfying the Cauchy-Condition! In $ℝ$ however we have peculiar circumstances and indeed real Cauchy-Sequences are always convergent, as we will prove in chapter 8.

Finaly we note the nesting theorem, a criterion that often copes successfully with 'difficult' sequences.

Proposition (nesting theorem): Let $(a_{n})$ , $(b_{n})$ and $(c_{n})$ be three sequences such that

a_{n} \leq b_{n} \leq c_{n} for all n \in ℕ^{*}

If $(a_{n})$ and $(c_{n})$ are convergent to the same limit g, i.e. $a_{n} \to g$ and $c_{n} \to g$ , then $(b_{n})$ also converges to g:

b_{n} \to g

[5.5.8]

Proof: We use the criterion [5.4.2]. Let $ε > 0$ be arbitrary. As $a_{n} \to g$ , we find an $n_{1} \in ℕ^{*}$ such that

g - ε < a_{n} < g + ε for all n \geq n_{1} .

Similar we get an $n_{2} \in ℕ^{*}$ with

g - ε < c_{n} < g + ε for all n \geq n_{2} .

Thus for all $n \geq n_{0} ≔ \max {n_{1}, n_{2}}$ the following estimates hold:

g - ε < a_{n} \leq b_{n} \leq c_{n} < g + ε

g - ε < b_{n} < g + ε

The latter estimate however proves the convergence $b_{n} \to g$ .

Consider:

'As usual' the premise may be extenuated to: $a_{n} \leq b_{n} \leq c_{n}$ for nearly all n.

Example:

\frac{\sin n}{n} \to 0

[5.5.9]

Proof: All sine figures are between −1 and 1 so that the following estimate holds for all n. With the noted convergences we get our result from the nesting theorem.

\begin{matrix} \underset{↓}{- \frac{1}{n}} & \leq \frac{\sin n}{n} \leq & \underset{↓}{\frac{1}{n}} \\ 0 & 0 \end{matrix}

This example is easily generalized. We only needed the boundedness of $(\sin n)$ and the fact that $(\frac{1}{n})$ is a zero sequence.

Proposition: If $(a_{n})$ is bounded and $(b_{n})$ convergent to zero, we have:

a_{n} \cdot b_{n} \to 0

[5.5.10]

Proof: Due to [5.5.6] we only need to show: $| a_{n} \cdot b_{n} | \to 0$ . As $(a_{n})$ is bounded we get an $s \in ℝ^{> 0}$ such that $| a_{n} | \leq s$ for all n. So we have:

0 \leq | a_{n} \cdot b_{n} | = | a_{n} | \cdot | b_{n} | \leq s \cdot | b_{n} |

With [5.5.6] we see that both $(b_{n})$ and $(| b_{n} |)$ are zero sequences as is $(s \cdot | b_{n} |)$ according [5.6.5]. Furthermore we obviously have $0 \to 0$ so that the assertion now holds by the nesting theorem.

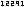5.4. 5.6.