5.4. Convergent Sequences

We start this new section with a closer look at our introductory sequence

(a_{n}) = (\frac{2 n + 1}{n + 1})

. Let us recall the table of values

with a detailed eye for the sequence members. First we note that each numerator is nearly twice the appropriate denominator, thus all sequence members are less than 2 in value. The difference between doubled denominator and numerator however is constantly 1 so the sequence members' difference from the number 2 is steadily decreasing.

We see this clearly noting them in their decimal representation and visualizing them on the real line:

The tendency for 2 becomes also obvious when calculating the distance - i.e. the difference in absolute value - of sequence members to 2. Take e.g. the 1000^th member:

| a_{1000} - 2 | = | \frac{2001}{1001} - 2 | = \frac{1}{1001} .

Thus the 1000^th sequence member and all to follow (note: the sequence is increasing) is closer to 2 than 0.001.

However to ensure that this sequence approaches the number 2 it isn't sufficient to choose some sequence members by chance and calculate their distance to 2 as small. The task has to be reversed instead: Are we able to prove that for each arbitrary distance $ε > 0$ nearly all sequence members are closer to 2 than $ε$ ?

We will show this for our example sequence. But to this end we first have to introduce a precise notation for the fact that 'a sequence $(a_{n})$ approaches a number g'.

The following definition is the base of all calculus.

Definition: Let $(a_{n})$ be any sequence and $g \in ℝ$ .

We call $(a_{n})$ convergent to g (in symbols: $a_{n} \to g$ ) if for each real $ε > 0$ there is a natural number $n_{0} \in ℕ^{*}$ such that

| a_{n} - g | < ε for all n \geq n_{0}

[5.4.1]

If $(a_{n})$ is convergent to g, we call g a limit of $(a_{n})$ . In this case the sequence $(a_{n})$ is convergent. Sequences with no limit are said to be divergent.

Consider:

Occasionally there is an advantage in rephrasing the definition of convergence. Obviously the distance of $a_{n}$ to g will be less than $ε$ if $a_{n}$ is at most $ε$ units away from g regardless if it is to the right or to the left. That means $a_{n}$ has to be in an open interval centered at g with radius $ε$ :

| a_{n} - g | < ε \Leftrightarrow a_{n} \in] g - ε, g + ε [

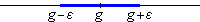
In this context we call these special intervals $\underline{ε -neighbourhoods}$ of g and restate the convergence condition as follows:

a_{n} \to g \Leftrightarrow

For every

ε > 0

there is an

n_{0} \in ℕ^{*}

,
such that

a_{n} \in] g - ε, g + ε [for all n \geq n_{0}

[5.4.2]

Now we can prove exactly that our initial sequence converges to 2:

Example:

$\frac{2 n + 1}{n + 1} \to 2$

Proof: Let $ε > 0$ be arbitrary. We need to find an $n_{0} \in ℕ^{*}$ so that all sequence members from $n_{0}$ on are closer to 2 than $ε$ . Let us see what they have to contribute to fulfill this demand:

\begin{array}{l} | a_{n} - g | < ε & \Leftrightarrow | \frac{2 n + 1}{n + 1} - 2 | < ε \\ \Leftrightarrow | \frac{2 n + 1 - 2 n - 2}{n + 1} | < ε \\ \Leftrightarrow | \frac{- 1}{n + 1} | < ε \\ \Leftrightarrow \frac{1}{n + 1} < ε \\ \Leftrightarrow \frac{1}{ε} < n + 1 \\ \Leftrightarrow \frac{1}{ε} - 1 < n \end{array}

So we have: The distance to 2 of a sequence member is less then $ε$ as soon as the index is more than $\frac{1}{ε} - 1$ . This information enables us to choose an appropriate $n_{0}$ : As $(n)$ is unbounded (cf. [5.3.21]), we can take an $n_{0} \in ℕ^{*}$ such that $n_{0} > \frac{1}{ε} - 1$ . For all $n \geq n_{0}$ this implies: $n > \frac{1}{ε} - 1$ . These n thus satisfy

| \frac{2 n + 1}{n + 1} - 2 | = | \frac{- 1}{n + 1} | = \frac{1}{n + 1} < ε

Consider:

When proving convergence we often need to cope with the request 'Now take an $n_{0} > \dots$ '. But as $ℕ$ is unbounded we can always make such a choice! For our comfort we will tacitly assume this argument in future proofs.

Although we now definitely know that $\frac{2 n + 1}{n + 1} \to 2$ we still can ask if $(\frac{2 n + 1}{n + 1})$ has further limits. From the original definition we don't get any information on the uniqueness of the limit, but it is easy to see that no sequence permits two limits:

Proposition:

Every sequence $(a_{n})$ has at most one limit.

[5.4.3]

Proof: Assume $g_{1}$ and $g_{2}$ are two different limits of $(a_{n})$ . Then their distance

r ≔ | g_{1} - g_{2} |

is non-negative. If we center at $g_{1}$ and at $g_{2}$ each an open interval with radius $\frac{r}{2}$ we get two $ε$ -neighbourhoods with no common elements. (+)

But as $a_{n} \to g_{1}$ we get from [5.4.2] a natural number $n_{1} \in ℕ^{*}$ such that all sequence members $a_{n}$ with an index $n \geq n_{1}$ are members of the first neighbourhood. Similar we see all members from an appropriate index $n_{2} \in ℕ^{*}$ onwards in the second neighbourhood.

Now set $n^{*} ≔ \max {n_{1}, n_{2}}$ . The sequence member $a_{n^{*}}$ thus belongs to both neighbourhoods, in contradiction to (+).

So we know that convergent sequences have exactly one limit. So we may introduce a symbol that only shows the data of $(a_{n})$ . If $a_{n} \to g$ we say that g is the limit of $(a_{n})$ and we denote this by:

lim a_{n} = g

, or more explicitely:

\lim_{n \to \infty} a_{n} = g

The convergence $\frac{2 n + 1}{n + 1} \to 2$ e.g. may now be noted like this:

lim \frac{2 n + 1}{n + 1} = 2

The question of convergence is always combined with the problem of divergence. From our alternative definition [5.4.2] we get a quite handy criterion for divergence.

Proposition:

$a_{n} \to g \Leftrightarrow$

each

ε

-neighbourhood

] g - ε, g + ε [

of g misses at most finitely many sequence members.

[5.4.4]

$a_{n} / \to g \Leftrightarrow$

there is one

ε

-neighbourhood

] g - ε, g + ε [

of g missing infinitely many sequence members.

[5.4.5]

Proof:

1. ►
" $\Rightarrow$ ": If $] g - ε, g + ε [$ is an arbitrary $ε$ -neighbourhood of g, [5.4.2] provides an $n_{0} \in ℕ^{*}$ such that $a_{n} \in] g - ε, g + ε [for all n \geq n_{0} .$ But that means that at most the sequence members $a_{1}, \dots, a_{n_{0} - 1}$ - and these are only finitely many - are missing in $] g - ε, g + ε [$ .

" $\Leftarrow$ ": If $ε > 0$ , the neighbourhood $] g - ε, g + ε [$ will miss at most finitely many members, say $a_{n_{1}}, \dots, a_{n_{k}}$ . If we set $n_{0} ≔ max {n_{1}, \dots, n_{k}} + 1$ all sequence members $a_{n}$ with $n \geq n_{0}$ will belong to $] g - ε, g + ε [$ . According [5.4.2] this proves the convergence $a_{n} \to g$ .

2. ►
This is just the negation of 1.

The following examples will play an important role in our further studies. The third one, by the way, uses our new criterion for 'non-convergent'.

Example:

$\frac{1}{n} \to 0$	[5.4.6]
For a given $ε > 0$ we take an $n_{0} > \frac{1}{ε}$ . Then we have for all $n \geq n_{0} :$ $n > \frac{1}{ε}$ and thus $\| \frac{1}{n} - 0 \| = \frac{1}{n} < ε$ .
$c \to c$ for each constant sequence $(c)$	[5.4.7]
If $ε > 0$ all sequence members with $n \geq n_{0} ≔ 1$ satisfy $\| c - c \| = 0 < ε$ .
$(n)$ ist divergent	[5.4.8]
We have to show: No real number $g \in ℝ$ is a limit of $(n)$ . But for each g the set ${n \in ℕ^{*} \| n \geq g + 1}$ is infinite, i.e. the special $ε$ -neighbourhood $] g - 1, g + 1 [$ misses infinitely many sequence members. With [5.4.2] we conclude: $n / \to g$ .

Even without our proof the divergence of $(n)$ is quite obvious: The natural numbers 'break away to the right', they can't concentrate on a fixed point in the end. There are many divergent sequences with a similar behaviour. The next example however shows a divergent sequence that is bounded. In that case divergence is due to the fact that the sequence can't decide where to go.

Example:

({(- 1)}^{n})

is divergent

[5.4.9]

Proof: Again we use our criterion [5.4.2].

The special $ε$ -neighbourhood $] 1 - 1, 1 + 1 [=] 0, 2 [$ of 1 misses infinitely many sequence members, namely all with an odd index. Thus at the very moment 1 is no limit of $({(- 1)}^{n})$ .

Now, if g is an arbitrary real different from 1, we have: $r ≔ | g - 1 | > 0$ . As r is the distance of g to 1 the neighbourhood $] g - r, g + r [$ will miss the number 1 and therefore all the infinitely many sequence members with an even index. So g is no limit of $({(- 1)}^{n})$ either.

Having no limit at all this sequence is divergent.

The convergence of a sequence describes the behaviour of the sequence members 'in the long run', so the 'first' members are of no significance in this respect. More precise we have the following:

Proposition: Let $(a_{n})$ be an arbitrary sequence. For each $k \in ℕ$ the following equivalence holds:

a_{n} \to g \Leftrightarrow a_{n + k} \to g

[5.4.10]

Proof:

" $\Rightarrow$ ": Let $ε > 0$ be given. As $a_{n} \to g$ we get an $n_{0} \in ℕ^{*}$ such that $| a_{n} - g | < ε$ for all $n \geq n_{0}$ . From $n + k \geq n \geq n_{0}$ we have for these n more than ever: $| a_{n + k} - g | < ε$ . This proves $a_{n + k} \to g$ .

" $\Leftarrow$ ": Let's start again with an $ε > 0$ . Now we have $a_{n + k} \to g$ , so we get an $n_{0} \in ℕ^{*}$ such that $| a_{n + k} - g | < ε$ for all $n \geq n_{0}$ . As all $n \geq n^{*} ≔ n_{0} + k$ satisfy $n - k \geq n_{0}$ we have for these n: $| a_{n} - g | = | a_{n - k + k} - g | < ε$ . Thus the convergence $a_{n} \to g$ is valid.

From our examples we see that the basic task in proving a certain convergence is to solve the inequality $| a_{n} - g | < ε$ for n. With more complicated sequences this leads fairly quick to unsolvable problems. It might be helpful to note that it isn't necessary to solve the inequality equivalently. It is rather sufficient instead to squeeze down the distance $| a_{n} - g |$ beneath $ε$ using the estimating technique. We illustrate this in our final example.

The next section will provide more comfortable utilities that often will replace efforts like the following.

Example:

$\frac{6 n^{2} + 2 n - 1}{3 n^{2} - n} \to 2$

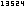Proof: For an arbitrary $ε > 0$ we take an $n_{0} > \frac{2}{ε}$ . Then we get for all $n \geq n_{0}$ :

\begin{array}{l} | \frac{6 n^{2} + 2 n - 1}{3 n^{2} - n} - 2 | & = | \frac{6 n^{2} + 2 n - 1 - 6 n^{2} + 2 n}{3 n^{2} - n} | \\ = \frac{4 n - 1}{3 n^{2} - n} \\ \leq \frac{4 n}{3 n^{2} - n} (numerator increased) \\ \leq \frac{4 n}{3 n^{2} - n^{2}} (denominator decreased) \\ = \frac{4 n}{2 n^{2}} \\ = \frac{2}{n} < ε \end{array}

5.3. 5.5.