Excursus: Binomial Coefficients and Pascal's triangle
For the binomial coefficient is introduced using the factorial operator ! :
|
[5.0.1] |
where . For we calculate n! by successively multiplying the numbers . In many cases the partition property is a valuable tool.
We read
|
Example:
-
|
To prove the generalized binomial theorem we need the following properties 1. and 4.
|
Proposition:
|
1.
|
[5.0.2] |
|
2.
|
[5.0.3] |
|
3.
|
[5.0.4] |
|
4.
|
[5.0.5] |
Proof: We just calculate every quotient as given by the definition.
|
1. ►
| |
|
2. ► |
|
|
3. ► |
|
|
4. ► |
|
|
|
|
From the condition we know that there are exactly n + 1 many binomial coefficients for each n.
So we have for
If we note down these results centered, row by row we are producing Pascal's triangle, the well known scheme which is expanded up to n = 4 below:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
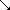 |
|
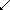 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
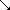 |
|
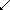 |
|
 |
|
 |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
| 1 |
|
|
|
4 |
|
|
|
6 |
|
|
|
4 |
|
|
|
1 |
The above properties 1. to 4. are well reflected in Pascal's triangle:
-
Each row starts with 1 and ends with 1.
-
The second number in each row is the line number.
-
Every row can be read from left to right and vice versa with no difference.
-
Apart from the first and last, every entry in a line is the sum of the two entries above.
That means: How far Pascal's triangle might have been constructed, we easily can add a new line without wasting time with the tedious factorials. Let's see how it works in our example:
Now that the binomial coefficients are at our hand, we easily get concrete binomial formulas from the generalized binomial theorem, take e.g. n = 3 and n = 4:
But there are many more properties to be deduced from the generalized binomial theorem.
Proposition:
|
1.
|
[5.0.6] |
|
2.
|
[5.0.7] |
|
3.
|
[5.0.8] |
Proof:
1. ►
.
2. ►
.
3. ►
|
These results could also be traced in Pascal's triangle:
-
Every row sum is a power of 2 with the line number for the exponent.
-
Every alterning row sum equals zero.
|
-
The result of each diagonal sum is noted underneath to the right of the last addend.
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
|
|
| 1 |
|
|
|
4 |
|
|
|
6 |
|
|
|
4 |
|
|
|
1 |
|
Another important field for the binomial coefficients is combinatorics. A key sentence here is the following:
|
Proposition:
Each set M with n elements has exactly many subsets with i elements:
|
[5.0.9] |
Proof: The case i = 0 is nearly done: M has only one subset with 0 elements, namely the empty set,
so the assertion follows from [5.0.2]. For we prove by induction:
The precondition leaves nothing to do here, because is now contradictory.
-
Let M be a set with n + 1 elements, say . We separate the system of all subsets N of M having i elements into two disjoint parts:
Those N, that do not contain . But these are exactly all i-subsets of the n-set . According to the induction hypothesis there are many of them.
-
Those N, that do contain . Let us assign the set to each of those. This is obviously a bijective mapping onto the system of all (i − 1)-subsets of , so we have many sets in this group.
All in all (cf. [5.0.5]) M has now many subsets with i elements.
|
From this and [5.0.6] we can deduce a statement on the number of all subsest of M, i.e. the power of the power set of M.
Each n-set M has exactly many subsets:
|
[5.0.10] |
|