5.2. Recursive Sequences and the Principle of Induction

Choosing

ℕ^{*}

as domain for our sequences has a wide effect mainly due to the well advanced arithmetic and ordering properties that come with the natural numbers. This structure is settled when constructing

ℕ

in set theory. From there we take the following characterization of

ℕ

Proposition:

$k \in ℕ \Rightarrow k = 0 \lor k = n + 1$ for a suitable $n \in ℕ$ .

Every non-empty subset of $ℕ$ has a smallest element.

[5.2.1]

That means:

Every non-zero natural number is the successor of another natural number.
Every non-empty collection of natural numbers has a first one.

Both of these properties already support the idea to get every natural number by successive counting starting with 0. The Principle of Induction makes this precise:

Proposition (Principle of Induction): Let A be an arbitrary subset of $ℕ$ so that

$0 \in A$

$n \in A \Rightarrow n + 1 \in A$

[5.2.2]
Then A is the whole of $ℕ$ , i.e.: $A = ℕ$ .

Proof: We proceed indirectly and assume: $A \neq ℕ$ . Then the difference $ℕ \ A$ is a non-empty subset of $ℕ$ and, following 2. in [5.2.1], has a smallest element, say $k \in ℕ \ A$ . From $0 \in A$ we conclude that $k \neq 0$ . According 1. in [5.2.1] we find a number $n \in ℕ$ so that $k = n + 1$ . Especially we have $n < k$ . As k is the smallest element of $ℕ \ A$ we thus know that n is no member of $ℕ \ A$ . But that means $n \in A$ and from the second condition in [5.2.2] we can conclude that $k = n + 1$ belongs to A. contradiction!

The induction principle is a very effective tool. A whole technique called proof by induction, is based on this principle. We take the proof of a so called summation formula as a first example to demonstrate this technique: Adding the odd intergers from 1 to $2 n + 1$ gives the following results for the different values of n:

n = 0	n = 1	n = 2	n = 3	n = 4	n = 5
1 = 1	1 + 3 = 4	1 + 3 + 5 = 9	1 + 3 + 5 + 7 = 16	1 + 3 + 5 + 7 + 9 = 25	1 + 3 + 5 + 7 + 9 + 11 = 36

Obviously each of the six results is a square number, namely the square of n + 1, the number of addends! We would gain an enormous advantage, especially for huge numbers, if this would be true for every n. Unfortunately however this assumption could not be proved the customary way because we have to prove infinitely many single assertions. But exactly that is performed by the induction principle.

Example: For all $n \in ℕ$ we have:

$\sum_{i = 0}^{n} (2 i + 1) = {(n + 1)}^{2}$
[5.2.3]

Proof:

Our task is, a bit awkwardly shaped, the following: Show that the set

A ≔ {n \in ℕ | \sum_{i = 0}^{n} (2 i + 1) = {(n + 1)}^{2}} \subset ℕ

i.e. the collection of all natural numbers satisfying [5.2.3] is all of $ℕ$ . But to that end we only need to check if the two conditions of the induction principle hold for A!

$0 \in A : \sum_{i = 0}^{0} (2 i + 1) = 1 = {(0 + 1)}^{2}$
$n \in A \Rightarrow n + 1 \in A :$ $n \in A$ means that this n actually satisfies $\sum_{i = 0}^{n} (2 i + 1) = {(n + 1)}^{2}$ . To show that n + 1 also belongs to A the equation $\sum_{i = 0}^{n + 1} (2 i + 1) = {(n + 1 + 1)}^{2} = {(n + 2)}^{2}$ has to be verified:

$\begin{matrix} \sum_{i = 0}^{n + 1} (2 i + 1) & = \sum_{i = 0}^{n} (2 i + 1) + 2 (n + 1) + 1 \\ = {(n + 1)}^{2} + 2 (n + 1) + 1 \\ = {(n + 1 + 1)}^{2} . \end{matrix}$

Thus $n + 1 \in A$ .

The principle of induction now guarantees: $A = ℕ$ . In other words our summation formular is actually true for all natural numbers.

Consider:

The just performed technique, splitting off the last addend,

$\sum_{i = 0}^{n + 1} (2 i + 1) = \sum_{i = 0}^{n} (2 i + 1) + \sum_{i = n + 1}^{n + 1} (2 i + 1) = \sum_{i = 0}^{n} (2 i + 1) + 2 (n + 1) + 1$

is the standard trick for sums and related expressions.
With proofs by induction it is a valuable advantage that the sentence to be proved - in our example the equation $\sum_{i = 0}^{n + 1} (2 i + 1) = {(n + 1 + 1)}^{2}$ - can be noted just from the start by inserting n + 1 for n.

We practise the principle of induction with further summation formulas and other examples. We do this however without the explicit formation of the set A and take the terms $0 \in A$ resp. $n \in A \Rightarrow n + 1 \in A$ only as a label for the two steps in a proof by induction:

$0 \in A$ for the base step
$n \in A \Rightarrow n + 1 \in A$ for the induction step.

Proposition (Summation formula for the geometric series): Let $q \in ℝ, q \neq 1$ , then every $n \in ℕ$ satisfies:

$\sum_{i = 0}^{n} q^{i} = \frac{1 - q^{n + 1}}{1 - q}$
[5.2.4]

Proof:

$0 \in A : \sum_{i = 0}^{0} q^{i} = q^{0} = 1 = \frac{1 - q^{0 + 1}}{1 - q} .$
$n \in A \Rightarrow n + 1 \in A :$
$\begin{matrix} \sum_{i = 0}^{n + 1} q^{i} & = \sum_{i = 0}^{n} q^{i} + q^{n + 1} \\ = \frac{1 - q^{n + 1}}{1 - q} + q^{n + 1} \\ = \frac{1 - q^{n + 1} + (1 - q) q^{n + 1}}{1 - q} \\ = \frac{1 - q^{n + 1} + q^{n + 1} - q^{n + 2}}{1 - q} \\ = \frac{1 - q^{n + 1 + 1}}{1 - q} . \end{matrix}$

The summation formula for the geometric series playes a very important role in calculus. This is also true for the generalization of common binomial formula which we will present in the next proposition. For the notation we need the binomial coefficients $(\begin{matrix} n \\ i \end{matrix})$ , for the slightly extensive proof we need two of their properties and a trick called index shift.

Proposition (Generalized Binomial Theorem): Let

a, b \in ℝ

, then

{(a + b)}^{n} = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n - i} b^{i}

[5.2.5]

holds for every $n \in ℕ$ .

Proof:

$0 \in A : {(a + b)}^{0} = 1 = (\begin{matrix} 0 \\ 0 \end{matrix}) a^{0 - 0} b^{0} = \sum_{i = 0}^{0} (\begin{matrix} 0 \\ i \end{matrix}) a^{0 - i} b^{i}$ .
$n \in A \Rightarrow n + 1 \in A :$
$\begin{matrix} {(a + b)}^{n + 1} & = {(a + b)}^{n} (a + b) \\ = (\sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n - i} b^{i}) a + (\sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n - i} b^{i}) b \\ = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n + 1 - i} b^{i} + \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n - i} b^{i + 1} \\ = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n + 1 - i} b^{i} + \sum_{i = 1}^{n + 1} (\begin{matrix} n \\ i - 1 \end{matrix}) a^{n + 1 - i} b^{i} \\ = (\begin{matrix} n \\ 0 \end{matrix}) a^{n + 1 - 0} b^{0} + \sum_{i = 1}^{n} (\begin{matrix} n \\ i \end{matrix}) a^{n + 1 - i} b^{i} + \sum_{i = 1}^{n} (\begin{matrix} n \\ i - 1 \end{matrix}) a^{n + 1 - i} b^{i} + (\begin{matrix} n \\ n \end{matrix}) a^{0} b^{n + 1} \\ = (\begin{matrix} n \\ 0 \end{matrix}) a^{n + 1 - 0} b^{0} + \sum_{i = 1}^{n} ((\begin{matrix} n \\ i \end{matrix}) + (\begin{matrix} n \\ i - 1 \end{matrix})) a^{n + 1 - i} b^{i} + (\begin{matrix} n \\ n \end{matrix}) a^{0} b^{n + 1} \\ = (\begin{matrix} n + 1 \\ 0 \end{matrix}) a^{n + 1 - 0} b^{0} + \sum_{i = 1}^{n} (\begin{matrix} n + 1 \\ i \end{matrix}) a^{n + 1 - i} b^{i} + (\begin{matrix} n + 1 \\ n + 1 \end{matrix}) a^{0} b^{n + 1} \\ = \sum_{i = 0}^{n + 1} (\begin{matrix} n + 1 \\ i \end{matrix}) a^{n + 1 - i} b^{i} . \end{matrix}$

Summation formulas are by far not the only sentences to be proved by induction. The following example deals with an inequality.

Proposition (Bernoulli Inequality): For every real number $x \geq - 1$ and any $n \in ℕ$ we have:

{(1 + x)}^{n} \geq 1 + n x

[5.2.6]

Proof:

$0 \in A : {(1 + x)}^{0} = 1 \geq 1 = 1 + 0 \cdot x$ .
$n \in A \Rightarrow n + 1 \in A :$ Assume the inequality ${(1 + x)}^{n} \geq 1 + n x$ is already valid. Multiplying with the (due to $x \geq - 1$ ) positive number $1 + x$ gives:

${(1 + x)}^{n} (1 + x) \geq (1 + n x) (1 + x)$ .

Thus we can argue as follows::

$\begin{matrix} {(1 + x)}^{n + 1} & = {(1 + x)}^{n} (1 + x) \\ \geq (1 + n x) (1 + x) \\ = 1 + n x + x + n x^{2} \\ \geq 1 + n x + x, note that n x^{2} \geq 0 \\ = 1 + (n + 1) x . \end{matrix}$

The initial value 0 used with principle of induction is determind by the set $ℕ$ . However we can modify the induction principle so that any integer k gets the option for the initial value:

Proposition: Let $k \in ℤ$ and A be any subset of $ℤ^{\geq k}$ so that

$k \in A$

$n \in A \Rightarrow n + 1 \in A$

[5.2.7]
then we have: $A = ℤ^{\geq k}$ .

Proof: Let us set $A' ≔ {i - k | i \in A}$ . A' then is a subset of $ℕ$ containing 0 and with every n the successor $n + 1$ as well. From the induction principle we have $A' = ℕ$ and thus $A = ℤ^{\geq k}$ .

Very close related to the induction principle is a certain construction method, often used with sequences, the so called definition by recursion. We need two steps for a sequence $(a_{n})$ to be constructed in this way: The initial step is to fix a value for the first sequence member $a_{1}$ . The second step is to introduce a general method to calculate any sequence member $a_{n + 1}$ from its predecessor $a_{n}$ . As an example the sequence $(a_{n})$ could be constructed by the statement:

a_{1} ≔ 1 \land a_{n + 1} ≔ 2 a_{n} .

From the recursion formula we see that every new sequence member is twice its predecessor. So we can calculate the sequence members one after the other:

(a_{n}) = (1,2,4,8,16,32, \dots) .

The following proposition introduces the Principle of Recursion.

Proposition (Principle of Recursion): For any $c \in A$ and any function $f : ℕ^{*} \times A \to A$ the statement

$a_{1} ≔ c \land a_{n + 1} ≔ f (n, a_{n})$
[5.2.8]

defines a sequence in A.

Proof: We need to show that [5.2.8] constitutes a function $a : ℕ^{*} \to A$ . First we show that every $n \in ℕ$ has got an image in A. We set

D ≔ {n \in ℕ^{*} | there is an element a_{n} \in A according to [5.2.8]}

As $a_{1} \in A$ is guaranted by the premise we have $1 \in D$ . Now if $n \in D$ , i.e. $a_{n} \in A$ the recursion formula assigns an element of A to the successor $n + 1$ , but that means $n + 1 \in D$ . Thus we have $D = ℕ^{*}$ according to the (generalized) induction principle.

Next we show that there is only one image for each n, applying the induction principle again: For the set

E ≔ {n \in ℕ^{*} | there is only one element a_{n} \in A according to [5.2.8]}

we have: $1 \in E$ , because there is no $n \in ℕ^{*}$ such that $1 = n + 1$ , so that there is no assignment in [5.2.8] except for $a_{1} = c$ . Now let $n \in E$ , thus $a_{n}$ is uniquely determined and so is $f (n, a_{n})$ (because f is a function!). Finally $n + 1$ has only one predecessor, namely n. From all that we conclude that $a_{n + 1}$ is uniquely determined, thus $n + 1$ also belongs to E which completes our induction and we have $E = ℕ^{*}$ .

Consider:

We rarely use the explicit data c and f to define a sequence recursively. It is common to note them just the way we did in our introductory example. Either notion however can be translated into the other. E.g. the statement $a_{1} = 1 \land a_{n + 1} = 2 a_{n}$ turns into:

$c = 1$ and $f : ℕ^{*} \times ℝ \to ℝ$ given by $f (n, x) = 2 x$ .

Vice versa the data, let's say $c = 0$ and $f : ℕ^{*} \times ℝ \to ℝ$ given by $f (n, x) = n + x$ , translate to

$a_{1} = 0 \land a_{n + 1} = n + a_{n}$ .
As with the induction principle and with the sequences, the principle of recursion is extendable to functions of the type $f : ℤ^{\geq k} \times A \to A$ .

The real advantage of recursive sequences lies in their ability to reflect dynamic situations. Let's say a certain species of bacteria needs one hour to double its stock. Starting with one bacterium we can perfectly calculate the number $a_{n}$ of bacteria living at the beginning of the der n-th hour by our initial recursive sequence.

As a clear disadvantage with recursive sequences we see the effort that is needed to calculate sequence members far from the start. To get e.g. the size of the bacteria population when 100 hours are over you need to calculate separately 100 sequence members before!

We practise the principle of recursion with some examples. Note that changing only the first sequence member could result in a complete different sequence.

Example:

$a_{1} ≔ 2 \land a_{n + 1} ≔ 3 a_{n} - 2$ gives the sequence $(2,4,10,28,82, \dots)$ , because
$a_{2} = 3 a_{1} - 2 = 3 \cdot 2 - 2 = 4$ ,

$a_{3} = 3 a_{2} - 2 = 3 \cdot 4 - 2 = 10$ ,

$a_{4} = 3 a_{3} - 2 = 3 \cdot 10 - 2 = 28 \dots$
$a_{1} ≔ 1 \land a_{n + 1} ≔ 3 a_{n} - 2$ gives the sequence $(1,1,1,1,1,1, \dots)$ .
$a_{1} ≔ \frac{1}{2} \land a_{n + 1} ≔ \frac{1}{a_{n} + 1}$ gives the sequence $(\frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}, \frac{8}{13}, \dots)$ .
$a_{0} ≔ 1 \land a_{n + 1} ≔ a_{n} \cdot (n + 1)$ produces the sequence of factorials:
${(1,1,2,6,24,120,720,5.040, \dots)}_{n \geq 0} = {(n!)}_{n \geq 0}$ .

Two special recursive sequences get names of their own.

Definition: Let $c, d, q \in ℝ$ . A recursive sequence ${(a_{n})}_{n \geq 0}$ of the shape

$a_{0} ≔ c \land a_{n + 1} ≔ a_{n} + d$ is called arithmetic.	[5.2.9]
$a_{0} ≔ c \land a_{n + 1} ≔ a_{n} \cdot q$ is called geometric.	[5.2.10]

Consider:

The new sequence members of an arithmetic sequence are calculated by adding the constant addend d.

The new sequence members of a geometric sequence are calculated by multiplying the constant factor q.

Proposition:

${(a_{n})}_{n \geq 0}$ is arithmetic $\Leftrightarrow$ there is a $d \in ℝ$ , such that ${(a_{n})}_{n \geq 0} = {(a_{0} + n d)}_{n \geq 0}$ .	[5.2.11]
${(a_{n})}_{n \geq 0}$ is geometric $\Leftrightarrow$ there is a $q \in ℝ$ , such that ${(a_{n})}_{n \geq 0} = {(a_{0} \cdot q^{n})}_{n \geq 0}$ .	[5.2.12]

Proof: We concentrate on 1. The second assertion is just a multiplicative version of the first one. We split the equivalence into two parts.

" $\Rightarrow$ ": Let c and d be reals such that

a_{0} = c \land a_{n + 1} = a_{n} + d

Now we show by induction: $a_{n} = a_{0} + n d$ for all $n \in ℕ$ .

$0 \in A : a_{0} = a_{0} + 0 \cdot d$ .
$n \in A \Rightarrow n + 1 \in A : a_{n + 1} = a_{n} + d = a_{0} + n d + d = a_{0} + (n + 1) d$ .

" $\Leftarrow$ ": Setting

b_{0} ≔ a_{0} \land b_{n + 1} ≔ b_{n} + d

gives an arithmetic sequence ${(b_{n})}_{n \geq 0}$ that satisfies the equality ${(b_{n})}_{n \geq 0} = {(b_{0} + n d)}_{n \geq 0}$ as demonstrated just before. From that we have:

{(a_{n})}_{n \geq 0} = {(a_{0} + n d)}_{n \geq 0} = {(b_{0} + n d)}_{n \geq 0} = {(b_{n})}_{n \geq 0}

so that ${(a_{n})}_{n \geq 0}$ coincides with an arithmetic sequence and thus is arithmetic itself.

Arithmetic and geometric sequences show are some interesting properties.

As $a_{n + 1} = a_{n} + d \Leftrightarrow a_{n + 1} - a_{n} = d$ , the difference of two consecutive members of an arithmetic sequence is a constant.:

${(a_{n})}_{n \geq 0}$ is arithmetic $\Leftrightarrow a_{n + 1} - a_{n} = d for all n \in ℕ$ .

Below we show: The members of an arithmetic sequence are the arithmetic mean of their neighbours.
As $a_{n + 1} = a_{n} \cdot q \Leftrightarrow \frac{a_{n + 1}}{a_{n}} = q$ the quotient of two consecutive members of geometric sequence in $ℝ^{\neq 0}$ a constant:

${(a_{n})}_{n \geq 0}$ is geometric $\Leftrightarrow \frac{a_{n + 1}}{a_{n}} = q for all n \in ℕ$ .

Next we show: The absolute value of a member of a geometric sequence is the geometric mean of its neighbours.

Proposition:

${(a_{n})}_{n \geq 0}$ is arithmetic $\Leftrightarrow a_{n + 1} = \frac{a_{n} + a_{n + 2}}{2} for all n \in ℕ$	[5.2.13]
${(a_{n})}_{n \geq 0}$ is geometric $\Leftrightarrow a_{n} \cdot a_{n + 2} \geq 0 \land \| a_{n + 1} \| = \sqrt{a_{n} \cdot a_{n + 2}} for all n \in ℕ$	[5.2.14]

Proof:

1. ►
" $\Rightarrow$ ": We employ the recursion formula $a_{n + 1} = a_{n} + d$ twice:

$\frac{a_{n} + a_{n + 2}}{2} = \frac{a_{n} + a_{n + 1} + d}{2} = \frac{a_{n} + d + a_{n + 1}}{2} = \frac{a_{n + 1} + a_{n + 1}}{2} = a_{n + 1}$ .

" $\Leftarrow$ ": We show by induction

$a_{n + 1} = a_{n} + a_{1} - a_{0} for all n \in ℕ$ .

Thus ${(a_{n})}_{n \geq 0}$ is represented as an arithmetic sequence with $c = a_{0} and d = a_{1} - a_{0} .$

$0 \in A : a_{1} = a_{0} + a_{1} - a_{0} .$

$n \in A \Rightarrow n + 1 \in A :$ First we have from [5.2.13]: $2 a_{n + 1} = a_{n} + a_{n + 2} .$ This allows the following equation:

$\begin{matrix} a_{n + 2} & = 2 a_{n + 1} - a_{n} \\ = 2 a_{n} + 2 (a_{1} - a_{0}) - a_{n} \\ = (a_{n} + a_{1} - a_{0}) + a_{1} - a_{0} \\ = a_{n + 1} + a_{1} - a_{0} . \end{matrix}$

2. ►
" $\Rightarrow$ ": We proceed as we did in 1., also employing the recursion formula twice:

$a_{n} \cdot a_{n + 2} = a_{n} \cdot a_{n + 1} \cdot q = a_{n} \cdot q \cdot a_{n + 1} = a_{n + 1} \cdot a_{n + 1} = a_{n + 1}^{2}$ .

As squares are positive we have $a_{n} \cdot a_{n + 2} \geq 0$ as a first conclusion. The remainder of the assertion now follows when we extract the root.

" $\Leftarrow$ ": For the proof of this direction we have to consider two cases:

$a_{1} = 0$ . Using $| a_{n + 1} | = \sqrt{a_{n} \cdot a_{n + 2}}$ we can show by induction: $a_{n} = 0$ for all $n \geq 1$ . Thus ${(a_{n})}_{n \geq 0} = {(a_{0},0,0,0, \dots)}_{n \geq 0}$ is a geometric sequence with $q = 0$ .

$a_{1} \neq 0$ . Now an inductive argument gives: $a_{n} \neq 0 for all n \in ℕ$ . From this we show

$a_{n + 1} = a_{n} \cdot \frac{a_{1}}{a_{0}} for all n \in ℕ$ ,

just the same way we did in 1., so that ${(a_{n})}_{n \geq 0}$ is a geometric sequence with $c = a_{0} \land q = \frac{a_{1}}{a_{0}} .$

$0 \in A : a_{1} = a_{0} \cdot \frac{a_{1}}{a_{0}} .$

$n \in A \Rightarrow n + 1 \in A :$ From [5.2.14] we get: $a_{n + 1}^{2} = a_{n} \cdot a_{n + 2},$ thus:

$\begin{matrix} a_{n + 2} & = \frac{a_{n + 1}^{2}}{a_{n}} \\ = \frac{a_{n + 1}}{a_{n}} \cdot a_{n + 1} \\ = \frac{a_{n + 1}}{a_{n}} \cdot a_{n} \cdot \frac{a_{1}}{a_{0}} \\ = a_{n + 1} \cdot \frac{a_{1}}{a_{0}} . \end{matrix}$

The next to last proposition touched an intersting, but often difficult problem: Does every recursive sequence allow a non-recursive representation? And if so, is there a general procedure for the transcription? It is very unlikely to find a solution for such a general problem, but from the arithmetic and geometric sequences we know that single solutions are possible. So we have to study a given sequence individually to get an idea for a suitable formula. Whatever way a result was found, the principle of induction is the standard tool for its verification.

Example: Let $(a_{n})$ be the recursive sequence given by

a_{1} ≔ \frac{1}{2} \land a_{n + 1} ≔ \frac{a_{n} + 1}{2},

i.e. $(a_{n}) = (\frac{1}{2}, \frac{3}{4}, \frac{7}{8}, \frac{15}{16}, \dots)$ . It is quite obvious that the denominators represent the powers of 2 and that each numerator is one unit less the denominator. Thus we have the idea:

(a_{n}) = (\frac{2^{n} - 1}{2^{n}})

Proof by induction:

$1 \in A : a_{1} = \frac{1}{2} = \frac{2^{1} - 1}{2^{1}}$
$n \in A \Rightarrow n + 1 \in A : a_{n + 1} = \frac{a_{n} + 1}{2} = \frac{\frac{2^{n} - 1}{2^{n}} + 1}{2} = \frac{2^{n} - 1 + 2^{n}}{2 \cdot 2^{n}} = \frac{2^{n + 1} - 1}{2^{n + 1}}$

The principle of recursion allows extensions in a varying manner. We could e.g. introduce two stage recursions: We provide the first two sequence members $a_{1}$ und $a_{2}$ and thus can use two predecessors when calculating further members.

Example: The recursive sequence given by

a_{1} ≔ 1, a_{2} ≔ 1 \land a_{n + 2} ≔ a_{n + 1} + a_{n}

[5.2.15]

is called Fibonacci sequence. Her members are calculated by adding the first two predecessors, so that the Fibonacci numbers start like this:

1,1,2,3,5,8,13,21,34,55, \dots

Another option is to consider recursive sequences in $ℝ^{2}$ .

Example: If the recursive sequence $((a_{n}, b_{n}))$ is given by

(a_{1}, b_{1}) ≔ (2, 1) \land (a_{n + 1}, b_{n + 1}) ≔ (a_{n} + b_{n}, a_{n} \cdot b_{n}),

we get the following table of values: $((a_{n}, b_{n})) = ((2,1), (3,2), (5,6), (11,30), (41,330), \dots)$ .

From the notation we see that a recursive sequence in $ℝ^{2}$ could be regarded as a coupled system of two recursive sequences in $ℝ$ . So we could as well have said: Let $(a_{n})$ and $(b_{n})$ be given by

a_{1} ≔ 2, b_{1} ≔ 1 \land a_{n + 1} ≔ a_{n} + b_{n}, b_{n + 1} ≔ a_{n} \cdot b_{n} .

For some years the theory of chaos gained a remarkable popularity, an absolute exception for a mathematical topic. A final example in this part introduces a recursive sequence in $ℝ^{2}$ which is closely related with this popularity:

Example: For a fixed pair of numbers $(c_{1}, c_{2}) \in ℝ$ we define the sequence $((a_{n}, b_{n}))$ recursively by

(a_{1}, b_{1}) ≔ (c_{1}, c_{2}) \land (a_{n + 1}, b_{n + 1}) ≔ (a_{n}^{2} - b_{n}^{2} + c_{1}, 2 a_{n} b_{n} + c_{2})

[5.2.16]

We get different value tables for different values of $(c_{1}, c_{2})$ . The following table shows three examples with the first sequence members and their distances $| (a_{n}, b_{n}) | = \sqrt{a_{n}^{2} + b_{n}^{2}}$ to the point of origin as well.

$(c_{1}, c_{2})$	$(a_{n}, b_{n})$	$\| (a_{n}, b_{n}) \|$

$(0, 0)$	$(0,0), (0,0), (0,0), (0,0), (0,0), \dots$	$0,0,0,0,0, \dots$
$(0, 1)$	$(0,1), (- 1,1), (0, - 1), (- 1,1), (0, - 1), (- 1,1), \dots$	$1,1.414,1,1.414,1, \dots$
$(1, 1)$	$(1,1), (1,3), (- 9,7), (32,127), \dots$	$1.414,3.162,11.4,130.97, \dots$

Whereas some values of $(c_{1}, c_{2})$ produce steadily increasing distances, see e.g. the last example, there may be others where the distances are bounded. If we mark all those initial values $(c_{1}, c_{2})$ in the plane where the distances do not exceed 2 we get an extraordinary subset of $ℝ^{2}$ , the so called Mandelbrot set. Graphical editing of its margin reveals an amazing beauty:

The (mathematical) amazement is even greater if we blow up sections of the Mandelbrot set and blow up again and again. It is rewarding to start a journey into the Mandelbrot set.

The Mandelbrot set is the most popular example of a so called fractal. There are many more examples for fractals on the web. This site has a very exhaustive link list.

To produce fractals of your own you need information and tools.

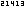5.1. 5.3.