Exkurs: Binomialkoeffizienten und Pascalsches Dreieck
Für ist der Binomialkoeffizient mit Hilfe Fakultätsoperators ! erklärt:
|
[5.0.1] |
dabei ist . Für ist also n! das fortlaufende Produkt der Zahlen . Oft benutzt man die folgende Zerlegungseigenschaft: .
Wir lesen
|
Beispiel:
-
|
Für den Beweis des allgemeinen Binomialtheorems benötigen wir die Eigenschaften 1. und 4. der folgenden Bemerkung.
|
Bemerkung:
|
1.
|
[5.0.2] |
|
2.
|
[5.0.3] |
|
3.
|
[5.0.4] |
|
4.
|
[5.0.5] |
Beweis: Wir rechnen jeweils die in der Definition angegebenen Quotienten aus.
|
1. ►
| |
|
2. ► |
|
|
3. ► |
|
|
4. ► |
|
|
|
|
Die Bedingung erzwingt, dass es zu jedem n genau n + 1 viele Binomialkoeffizienten gibt.
Man errechnet also z.B. für
Schreibt man nun diese Ergebnisse zeilenweise untereinander und richtet die Zeilen dabei zentriert aus, entsteht das bekannte Pascalsche Dreieck, das hier bis zur Zeile n = 4 notiert ist:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
 |
|
 |
|
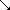 |
|
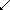 |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
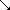 |
|
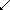 |
|
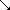 |
|
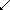 |
|
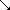 |
|
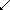 |
|
|
|
| 1 |
|
|
|
4 |
|
|
|
6 |
|
|
|
4 |
|
|
|
1 |
Im Pascalschen Dreieck lassen sich die Aussagen 1. bis 4. direkt ablesen:
-
Jede Zeile beginnt und endet mit 1.
-
Die zweite Zahl einer jeden Zeile ist die Zeilennummer.
-
Jede Zeile liest sich von links genauso wie von rechts.
-
Bei jeder neuen Zeile ergeben sich die Einträge, von den beiden Einsen abgesehen, durch Addition der beiden oberhalb stehenden Einträge der Vorzeile.
Das bedeutet: Jedes Pascalsche Dreieck kann mühelos, d.h. ohne die Fakultäten auszurechnen, durch eine weitere Zeile ergänzt werden. In unserem Fall etwa durch
Mit Kenntnis der Binomialkoeffizienten lassen sich nun nach dem allgemeinen Binomialtheorem konkrete binomische Formeln aufstellen, etwa für n = 3 und n = 4:
Aus dem allgemeinen Binomialtheorem lassen sich aber noch weitere Eigenschaften der Binomialkoeffizienten ableiten.
Bemerkung:
|
1.
|
[5.0.6] |
|
2.
|
[5.0.7] |
|
3.
|
[5.0.8] |
Beweis:
1. ►
.
2. ►
.
3. ►
|
Auch diese Ergebnisse lassen sich als Eigenschaften des Pascalschen Dreiecks deuten:
-
Jede Zeilensumme ist eine Zweierpotenz mit der Zeilennummer im Exponenten.
-
Jede alternierende Zeilensumme ist gleich Null.
|
-
Das Ergebnis jeder Diagonalsumme findet man rechts unterhalb des letzten Summanden:
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
|
|
| 1 |
|
|
|
4 |
|
|
|
6 |
|
|
|
4 |
|
|
|
1 |
|
Eine wichtige Rolle spielen die Binomialkoeffizienten auch bei kombinatorischen Fragen. Entscheidend ist dabei die folgende Aussage.
|
Bemerkung:
Jede Menge M mit n Elementen hat genau viele i-elementige Teilmengen:
|
[5.0.9] |
Beweis: Der Fall i = 0 ist schnell erledigt: M besitzt nur eine Teilmenge mit 0 Elementen, nämlich die leere Menge,
so dass die Behauptung aus [5.0.2] folgt. Für führen wir den Nachweis per Induktion:
Unter der Vorbedingung ist hier nichts zu zeigen, denn die Voraussetzung ist jetzt nicht erfüllbar.
-
Sei jetzt M eine Menge mit n + 1 vielen Elementen, etwa . Das System der i-elementigen Teilmengen von M zerlegen wir in zwei disjunkte Gruppen:
Diejenigen N, die nicht enthalten. Das sind aber genau alle i-elementigen Teilmengen der n-elementigen Menge . Nach Induktionsvoraussetzung sind dies viele.
-
Diejenigen N, die enthalten. Jedem solchen N ordnen wir nun die Menge zu. Da dies eine bijektive Abbildung in das System der (i − 1)-elementigen Teilmengen von ist,
gibt es in dieser Gruppe genau viele Mengen.
Insgesamt (siehe [5.0.5]) besitzt M also viele i-elementige Teilmengen.
|
Als Folgerung ergibt sich mit [5.0.6] daraus eine Aussage über die Anzahl aller Teilmengen von M, also über die Mächtigkeit der Potenzmenge von M.
Jede n-elementige Menge M hat genau viele Teilmengen:
|
[5.0.10] |
|