5.2. Rekursive Folgen und das Induktionsprinzip
Durch die Wahl der Menge als Definitionsbereich für unsere Folgen ergeben sich weit reichende Möglichkeiten, die i.w. auf die reichhaltige Rechen- und Anordnungstruktur der natürlichen Zahlen zurückzuführen sind.
Diese Struktur wird mit der Konstruktion von im Rahmen der Mengenlehre festegelegt. Wir übernehmen von dort die folgende Charakterisierung von :
|
Bemerkung:
-
für ein .
-
Jede nicht-leere Teilmenge von
besitzt ein kleinstes Element.
|
|
[5.2.1] |
|
Das bedeutet nun:
-
Jede von 0 verschiedene natürliche Zahl ist Nachfolger einer anderen natürlichen Zahl.
-
Jede nicht-leere Auswahl von natürlichen Zahlen besitzt ein Anfangselement.
Diese beiden Eigenschaften beinhalten bereits die Vorstellung, dass
man alle natürlichen Zahlen, beginnend bei 0, durch fortlaufendes
Weiterzählen erhalten kann. Das Induktionsprinzip präzisiert diese Vorstellung:
|
Bemerkung (Induktionsprinzip): Ist A eine Teilmenge von mit den beiden folgenden Eigenschaften
-
-
|
|
[5.2.2] |
so ist A bereits ganz , d.h.: .
Beweis: Wir gehen indirekt vor und nehmen an: . Dann ist aber die Restmenge eine nicht-leere Teilmenge von , besitzt also nach 2. in [5.2.1] ein kleinstes Element, etwa . Da , ist . Also gibt es gemäß 1. in [5.2.1] ein , so dass . Insbesondere ist . Da aber k kleinstes Element von ist, kann n nicht zu gehören. Also ist und daher gehört nach der 2. Bedingung in [5.2.2] auch zu A. Widerspruch!
|
Das Induktionsprinzip ist ein ungemein wirkungsvolles Instrument. Eine ganze
Beweistechnik, der Beweis per Induktion, baut auf dieses Prinzip.
Wir zeigen dies in einem ersten Beispiel am Beweis einer sog. Summenformel:
Addiert man die ungeraden natürlichen Zahlen von 1 bis der Reihe nach, so ergeben sich
für verschiedene Werte von n die folgenden Ergebnisse:
|
n = 0 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
1
= 1 |
1 + 3
= 4 |
1 + 3 + 5
= 9 |
1 + 3 + 5 + 7
= 16 |
1 + 3 + 5 + 7 + 9
= 25 |
1 + 3 + 5 + 7 + 9 + 11
= 36 |
Augenscheinlich ist in diesen sechs Fällen der Summenwert stets eine
Quadratzahl, und zwar das Quadrat der Anzahl n + 1 der Summanden! Wäre
dies für jedes n genauso, hätte man insbesondere bei
großen Zahlen einen erheblichen Rechenvorteil. Ein herkömmlicher
Beweis ist für diese Vermutung aber nicht zu führen, denn hier
sind unendlich viele Einzelaussagen zu beweisen; mit Hilfe des Induktionsprinzips
jedoch kann man genau das erreichen.
|
Beispiel: Für alle gilt:
|
[5.2.3] |
Beweis:
Die Aufgabe läßt sich, wenn auch etwas umständlich, folgendermaßen formulieren:
Weise nach, dass die Menge
,
also die Menge derjenigen natürlichen Zahlen, die die Behauptung in [5.2.3] erfüllen, ganz ist. Dazu müssen wir aber nur nachweisen, dass A die beiden Bedingungen des Induktionsprinzips erfüllt!
Gemäß Induktionsprinzip weiß man nun: . Also ist unsere Summenformel tatsächlich für alle natürlichen Zahlen gültig.
|
Beachte:
Die gerade im Beweis vorgenommene Zerlegung, das Abspalten des letzten Summanden,
ist bei Summen und ähnlichen strukturierten Ausdrücken der Standardtrick.
Es ist ein bei Induktionsbeweisen nicht zu unterschätzender Vorteil, dass man die zu beweisende Aussage - hier die Gleichung - bereits zu Beginn durch "Einsetzen von n + 1" notieren kann.
Wir üben das Induktionsprinzip an weiteren Summenformeln und anderen Beispielen. Dabei verzichten
wir auf die explizite Bildung der Menge A und benutzen die Ausdrücke
bzw.
nur noch als Markierungen für die beiden Induktionsschritte:
-
für den Induktionsanfang
-
für den Induktionsschluss.
|
|
Bemerkung (Summenformel für die geometrische Reihe): Es sei , dann gilt für alle :
|
[5.2.4] |
Beweis:
|
Die Summenformel für die geometrische Reihe ist in der Analysis ein äußerst wichtiges Ergebnis. Dies trifft genauso auf die in der folgenden Bemerkung vorgestellte Verallgemeinerung der ersten binomischen Formel zu.
Zu ihrer Formulierung benötigt man die Binomialkoeffizienten , zu ihrem (etwas umfangreichen) Beweis zwei ihrer Eigenschaften, sowie den "Trick" der Indexverschiebung bei der Summation.
Bemerkung (Allgemeines Binomialtheorem): Es sei , dann gilt für alle :
|
[5.2.5] |
Beweis:
|
Summenformeln sind bei weitem nicht die einzigen Aussagen, die per Induktion gesichert werden können. Im folgenden Beispiel etwa werden wir eine Ungleichung beweisen.
|
Bemerkung (Bernoullische Ungleichung): Für jede reelle Zahl und jedes gilt:
|
[5.2.6] |
Beweis:
.
Sei jetzt die Ungleichung bereits gültig. Multipliziert man sie mit der (wegen ) positiven Zahl , erhält man:
,
so dass wir die folgende Ungleichungskette aufstellen können:
|
Der Startwert 0 beim Induktionsprinzip ist durch die Menge festgelegt. Es ist allerdings möglich das
Induktionsprinzip so zu modifizieren, dass eine beliebige ganze Zahl k als Startwert eingesetzt werden kann:
|
Bemerkung: Ist und A eine Teilmenge von mit den beiden folgenden Eigenschaften
-
-
|
|
[5.2.7] |
so ist bereits .
Beweis: Setzt man
, so ist A' eine Teilmenge von , die die Zahl 0 enthält und mit jedem n auch die nächste Zahl .
Nach dem Induktionsprinzip ist also und somit .
|
Mit dem Induktionsprinzip sehr eng verwandt ist eine bei Folgen oft eingesetzte
Konstruktionsmethode, nämlich die Folgenangabe per Rekursion.
Dabei definiert man eine Folge in zwei Schritten:
zunächst setzt man einen Wert für das erste Folgenglied fest und gibt anschließend an, wie ein beliebiges Folgenglied aus seinem Vorgänger
entstehen soll. So könnte man z.B. eine Folge angeben durch die Festsetzung:
Jedes neue Folgenglied entsteht also durch Verdoppeln des Vorgängers, so dass man der Reihe nach die ersten Folgenglieder errechnen kann:
Mit der folgenden Bemerkung führen wir das
Rekursionsprinzip ein:
|
Bemerkung (Rekursionsprinzip): Für jedes und jede Funktion wird durch die Angabe
|
[5.2.8] |
eine Folge in A definiert.
Beweis: Es ist zu überlegen, dass mit [5.2.8] eine Funktion gegeben ist. Zunächst zeigen wir dass jedem ein Element aus A zugeordnet ist und bilden dazu die Menge
.
Da festgelegt ist, weiß man: . Ist ferner , also gegeben, so wird über die Rekursionsvorschrift auch der Nachfolgerzahl ein Bild aus A zugewiesen, d.h. aber . Nach dem (erweiterten) Induktionsprinzip ist damit .
Als nächstes zeigen wir, dass jedem n auch nur ein Bild zugewiesen ist und setzen dabei wieder das Induktionsprinzip ein: Für die Menge
hat man nämlich: , denn für kein ist , so dass außer über die Festsetzung in [5.2.8] keine weitere
Zuweisung erfolgt ist. Ist nun , also eindeutig definiert, so gibt es auch nur
einen Wert (denn f ist ja eine Funktion!). Schließlich hat auch nur einen Vorgänger, nämlich n, so dass auch eindeutig erklärt ist. Also ist auch in E. Insgesamt ist daher .
|
Beachte:
-
Rekursiv notierte Folgen werden selten über die expliziten Daten c und f angegeben sondern oft in der Form unseres Eingangsbeispiels. Beide Schreibweisen lassen sich
aber ineinander überführen. So wird etwa die Angabe zu:
und ist gegeben durch .
Umgekehrt schreibt man z.B. und , gegeben durch , als
.
-
Das Rekursionsprinzip läßt sich - wie der Folgenbegriff und das Induktionsprinzip auch - auf Funktionen der Art erweitern.
Der große Vorteil des Rekursionsprinzips zeigt sich, wenn man "dynamische"
Situationen beschreiben will. Weiß man z.B. dass eine bestimmte
Bakterienart eine Stunde benötigt, um ihren Bestand zu verdoppeln, so
wird man - von einem Bakterium ausgehend - die Anzahl
der zu Beginn der n-ten Stunde vorhandenen Bakterien
(idealisiert) durch unsere erste Rekursion angeben können.
Als Nachteil gilt bei rekursiven Folgen, die Schwierigkeit weit hinten liegende
Folgenglieder zu ermitteln. Um etwa die Größe der Bakterienpopulation
nach 100 Stunden zu ermitteln, müssen zuvor 100 Folgenglieder der Reihe
nach ermittelt werden!
Wir üben zunächst das Rekursionsprinzip an einigen Beispielen. Interessant ist dabei die Beobachtung, dass allein eine Änderung des ersten Folgenglieds zu einer völlig neuen Folge führen kann.
|
Beispiel:
erzeugt die Folge , denn
,
,
-
erzeugt die Folge
.
-
erzeugt die Folge .
-
liefert die Folge der Fakultäten:
.
|
Zwei spezielle rekursive Folgen zeichnen wir durch einen eigenen Namen aus.
|
Definition: Es sei . Eine rekursive gegebene Folge
der Form
-
heißt arithmetisch.
|
[5.2.9] |
-
heißt geometrisch.
|
[5.2.10] |
|
Beachte:
Die neuen Folgenglieder einer arithmetischen Folge entstehen also durch Addition des konstanten Summanden d.
Die neuen Folgenglieder einer geometrischen Folge entstehen durch Multiplikation mit dem konstanten Faktor q.
|
Bemerkung:
-
ist arithmetisch
es gibt ein , so dass .
|
[5.2.11]
|
-
ist geometrisch
es gibt ein , so dass .
|
[5.2.12] |
Beweis: Wir zeigen nur 1., denn die zweite Aussage ist i.W. nur die multiplikative Kopie der ersten.
Die Äquivalenz teilen wir dabei in zwei Schritte auf.
"": Es gibt also reelle Zahlen c und d, so dass
.
Wir zeigen jetzt per Induktion: für alle .
.
.
"": Setzt man jetzt
,
so ist dadurch eine arithmetische Folge gegeben, die nach dem gerade bewiesenen Teil die Gleichung erfüllt. Dies aber können wir weiter schreiben zu:
.
ist also mit einer arithmetischen Folge identisch und somit selbst arithmetisch.
|
Arithmetische und geometrische Folgen besitzen einige interessante Eigenschaften.
-
Da , ist bei arithmetischen Folgen ist die Differenz zweier aufeinander folgender Glieder konstant:
ist arithmetisch .
In der nächsten Bemerkung zeigen wir:
Die Glieder einer arithmetischen Folge sind das arithmetische Mittel ihrer Nachbarglieder.
-
Da , ist bei geometrischen Folgen in der Quotient zweier aufeinander folgender Glieder konstant:
ist geometrisch .
Wir zeigen noch: Die Glieder einer geometrischen Folge sind dem Betrag nach das geometrische Mittel ihrer Nachbarglieder.
|
Bemerkung:
-
ist arithmetisch
|
[5.2.13]
|
-
ist geometrisch
|
[5.2.14] |
Beweis:
|
1. ►
|
"": Wir setzen die Rekursionsvorschrift zweimal ein:
.
"": Wir zeigen jetzt per Induktion
und haben so als eine arithmetische Folge mit dargestellt.
Zunächst ergibt sich aus der Bedingung in [5.2.13]: , so dass wir die folgende Gleichung aufstellen können:
|
|
2. ►
|
"": Wir gehen analog zu 1. vor und wenden auch hier die Rekursionsvorschrift zweimal an:
.
Damit ergibt sich zunächst: . Die restliche Behauptung erhält man anschließend durch Wurzelziehen.
"": Beim Nachweis dieser Richtung sind zwei Fälle zu unterscheiden:
-
, dann ergibt sich aus mittels Induktion für alle . ist also eine geometrische Folge mit .
-
. Jetzt erhält man per Induktion: . Analog zu 1. können wir damit zeigen
,
so dass eine geometrische Folge mit ist.
Aus [5.2.14] erhalten wir: , und damit:
|
|
In der vorletzten Bemerkung ist ein interessantes, aber oft schwieriges Problem
angesprochen: Im Prinzip läßt sich jede rekursiv gegebene
Folge auch auch nicht-rekursiv darstellen. Gibt es ein allgemeines Verfahren,
diese Umschreibung auch tatsächlich durchzuführen? In dieser
Allgemeinheit wird man kaum eine positive Anwort finden; in speziellen
Situationen, wie etwa bei den geometrischen oder arihtmetischen Folgen, kann
man aber durchaus Erfolg haben. Meist jedoch wird man jede Folge individuell
untersuchen müssen, um eine Idee für eine geeignete Folgenvorschrift
zu finden. In jedem Fall allerdings ist das Induktionsprinzip das
Beweismittel, um die Gültigkeit der rekursionsfreien Darstellung beweisen zu
können.
|
Beispiel: sei rekursiv gegeben durch
also . Man erkennt deutlich dass im Nenner die 2-er Potenzen stehen und dass der Zähler stets um 1 niedriger ausfällt als der Nenner.
Man vermutet daher:
Beweis per Induktion:
|
Das Rekursionsprinzip läßt sich vielfältig erweitern. So
kann man etwa zweistufige Rekursionen einführen: Man gibt dabei die
ersten zwei Folgenglieder und vor und kann dann bei der Ermittlung der weiteren Glieder auf zwei Vorgänger
zurück greifen.
|
Beispiel: Die durch
|
[5.2.15] |
rekursiv gegebene Folge heißt Fibonacci-Folge. Ihre Folgenglieder entstehen jeweils durch Addition der beiden Vorgänger. Die ersten Fibonacci-Zahlen berechnet man also zu:
.
|
Eine weitere Möglichkeit besteht darin, rekursive Folgen in zu betrachten.
|
Beispiel: Ist die Folge rekursiv gegeben durch
so ergibt sich die folgende Wertetabelle:
.
Die Schreibweise zeigt, dass man eine rekursive Folge
in auch auffassen kann als ein gekoppeltes System zweier rekursiver Folgen in . Man hätte also auch schreiben
können: und seien rekursiv gegeben durch
|
In den letzten Jahren hat die sog. Chaos-Theorie einen - für
ein mathematisches Thema - außergewöhnlich hohen Bekanntheitsgrad
erreicht. Ein letztes Beispiel in diesem Abschnitt stellt eine rekursive
Folge in vor, die mit der Popularität dieser Theorie eng verbunden ist:
|
Beispiel: Für ein (festes) Zahlenpaar sei die Folge rekursiv gegeben durch
|
[5.2.16] |
Für verschiedene Werte von ergeben sich nun unterschiedliche Wertetabellen. In der folgenden Tafel sind neben ersten Folgengliedern auch deren Abstände zum Koordinatenursprung notiert.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Während nun bei einigen Werten von die Nullabstände immer
größer werden, wie etwa im letzten Beispiel, liefern andere Startwerte
solche Abstände, die eine gewisse Schranke nicht überschreiten.
Markiert man nun in der Zeichenebene etwa all diejenigen Punkte bei denen die Nullabstände
der resultierenden Folgen den Wert 2 nicht übertreffen, ergibt sich
eine äußerst interessante Teilmenge des , die sog.
Mandelbrotmenge. Bereitet man auch die Randbereiche dieser Menge graphisch
auf, entsteht eine optische sehr faszinierende Darstellung:

Mathematisch interessant wird die Mandelbrotmenge erst, wenn man Ausschnitte
von ihr vergrößert und wieder vergrößert und noch mal
vergößert usw. Es lohnt sich, eine
Reise durch die
Mandelbrotmenge zu unternehmen.
Die Mandelbrotmenge ist das bekannteste Beispiel eines sog. Fractals.
Es gibt viele weitere Beispiele von Fractalen im web. Diese Seite enthält eine sehr(!) umfangreiche link-Liste zu phantastischen fractal sites.
Wer selbst Fractale erstellen will, kann sich
hier informieren
und die nötigen tools bekommen.
|
|
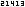 |
|
