Beispiele zum Lagrange-Verfahren

Wir illustruieren das Lagrange-Verfahren an einigen Beispielen in

ℙ (ℝ)

. Dazu geben wir jeweils Stützpunkte

(x_{0}, y_{0}), \dots, (x_{n}, y_{n})

vor, stellen die dazu gehörigen Lagrangeschen Grundpolynome

l_{k} = \prod_{\begin{matrix} i = 0 \\ i \neq k \end{matrix}}^{n} \frac{X - x_{i}}{x_{k} - x_{i}} = \frac{(X - x_{0}) \cdot \dots \cdot (X - x_{k - 1}) \cdot (X - x_{k + 1}) \cdot \dots \cdot (X - x_{n})}{(x_{k} - x_{0}) \cdot \dots \cdot (x_{k} - x_{k - 1}) \cdot (x_{k} - x_{k + 1}) \cdot \dots \cdot (x_{k} - x_{n})}

auf und ermitteln anschließend das Lagrangesche Interpolationspolynom $p = y_{0} l_{0} + \dots + y_{n} l_{n}$ .

Beispiel:

Für die vorgegebenen Stützpunkte (2 , 4) , (6 , 6) ist

$\begin{array}{l} l_{0} = \frac{X - 6}{2 - 6} = - \frac{1}{4} (X - 6) \\ l_{1} = \frac{X - 2}{6 - 2} = \frac{1}{4} (X - 2) . \end{array}$

Damit hat man: $p = 4 l_{0} + 6 l_{1} = - \frac{4}{4} (X - 6) + \frac{6}{4} (X - 2) = \frac{1}{2} X + 3$ .
Für die vorgegebenen Stützpunkte (0 , 2) , (1 , 4) , (−1 , 6) ist

$\begin{array}{l} l_{0} = \frac{(X - 1) \cdot (X + 1)}{(0 - 1) \cdot (0 + 1)} = - (X^{2} - 1) \\ l_{1} = \frac{(X - 0) \cdot (X + 1)}{(1 - 0) \cdot (1 + 1)} = \frac{1}{2} (X^{2} + X) \\ l_{2} = \frac{(X - 0) \cdot (X - 1)}{(- 1 - 0) \cdot (- 1 - 1)} = \frac{1}{2} (X^{2} - X) . \end{array}$

Also: $p = 2 l_{0} + 4 l_{1} + 6 l_{2} = - 2 (X^{2} - 1) + \frac{4}{2} (X^{2} + X) + \frac{6}{2} (X^{2} - X) = 3 X^{2} - X + 2$ .
Für die vorgegebenen Stützpunkte (1 , 1) , (2 , 2) , (3 , 3) ist

$\begin{array}{l} l_{0} = \frac{(X - 2) \cdot (X - 3)}{(1 - 2) \cdot (1 - 3)} = \frac{1}{2} (X^{2} - 5 X + 6) \\ l_{1} = \frac{(X - 1) \cdot (X - 3)}{(2 - 1) \cdot (2 - 3)} = - (X^{2} - 4 X + 3) \\ l_{2} = \frac{(X - 1) \cdot (X - 2)}{(3 - 1) \cdot (3 - 2)} = \frac{1}{2} (X^{2} - 3 X + 2) . \end{array}$

Also: $p = l_{0} + 2 l_{1} + 3 l_{2} = \frac{1}{2} (X^{2} - 5 X + 6) - 2 (X^{2} - 4 X + 3) + \frac{3}{2} (X^{2} - 3 X + 2) = X$ .

Mit dem folgenden Formular lässt sich das Lagrangesche Interpolationspolynom zu beliebigen Stützpunkten ermitteln. Zunächst gibt man sie der Reihe nach ein (Stützpunkte sind nach Anklicken korrigier- bzw. löschbar):

diesen Stützpunkt mit ↲ oder Klick speichern.

Anschließend können die Lagrangeschen Grundpolynome $l_{k}$ und das Interpolationspolynom p per Klick auf →Ergebnis abgerufen werden. (Koeffizienten auf 4 Stellen gerundet)

Mit dem Lagrange-Verfahren lassen sich zwei vertraute Eigenschaften linearer Funktionen neu beweisen.

Bemerkung:

Zu jedem Punkt $(x, c)$ gibt es genau eine konstante Funktion, die durch $(x, c)$ geht.	[4.0.6]
Zu je zwei Punkten $(x_{1}, y_{1})$ und $(x_{2}, y_{2})$ mit unterschiedlichen x-Werten gibt es genau eine lineare Funktion die durch $(x_{1}, y_{1})$ und $(x_{2}, y_{2})$ geht.	[4.0.7]

Beweis:

1. ► Beachtet man die Konvention, dass ein Produkt aus 0 Faktoren gleich 1 ist, so gilt für das erste (und einzige) Lagrangesche Grundpolynom: $l_{0} = 1$ . Also ist $p = c \cdot 1 = c$ .

2. ► Mit $l_{0} = \frac{X - x_{2}}{x_{1} - x_{2}}$ und $l_{1} = \frac{X - x_{1}}{x_{2} - x_{1}}$ ergibt sich die sog. 2-Punkte-Form:

p = y_{1} l_{0} + y_{2} l_{1} = y_{1} \frac{X - x_{2}}{x_{1} - x_{2}} + y_{2} \frac{X - x_{1}}{x_{2} - x_{1}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} X + \frac{y_{1} x_{2} - y_{2} x_{1}}{x_{2} - x_{1}}

Durch Umformen des letzten Summanden

\frac{y_{1} x_{2} - y_{2} x_{1}}{x_{2} - x_{1}} = \frac{y_{1} x_{2} - y_{2} x_{2} + y_{2} x_{2} - y_{2} x_{1}}{x_{2} - x_{1}} = - \frac{y_{2} - y_{1}}{x_{2} - x_{1}} x_{2} + y_{2}

erhalten wir eine kompakte Darstellung der 2-Punkte Form, die sich leichter merken lässt:

p = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (X - x_{2}) + y_{2}

Gelegentlich benutzt man die Lagrangesche Methode um eine andere Funktionen f durch Polynome zu interpolieren. Als Stützpunkte wählt man dabei Graphenpunkte von f, also Punkte der Form

(x_{0}, f (x_{0})), \dots, (x_{n}, f (x_{n}))

Dabei wird die gewünschte Interpolation (möglicherweise) um so besser sein, je mehr Stützpunkte ausgewählt wurden.

Als Beispiel ermitteln wir für die Betragsfunktion $| X |$ zwei Interpolationspolynome, eins für drei und eins für fünf Stützpunkte. Wir beginnen mit (−1 , | −1 |) , (0 , | 0 |) , (1 , | 1 |), also mit (−1 , 1) , (0 , 0) , (1 , 1):

\begin{array}{l} l_{0} = \frac{(X - 0) \cdot (X - 1)}{(- 1 - 0) \cdot (- 1 - 1)} = \frac{1}{2} (X^{2} - X) \\ l_{1} = \frac{(X + 1) \cdot (X - 1)}{(0 + 1) \cdot (0 - 1)} = - (X^{2} - 1) \\ l_{2} = \frac{(X + 1) \cdot (X - 0)}{(1 + 1) \cdot (1 - 0)} = \frac{1}{2} (X^{2} + X) \end{array}

Daraus erhält man das erste Interpolationspolynom (für drei Stützpunkte):

p_{3} = l_{0} + 0 l_{1} + l_{2} = X^{2}

Im zweiten Schritt fügen wir $(- \frac{1}{2}, | - \frac{1}{2} |)$ und $(\frac{1}{2}, | \frac{1}{2} |)$ als weitere Stützpunkte ein . Wir gehen also aus von $(- 1,1), (- \frac{1}{2}, \frac{1}{2}), (0,0), (\frac{1}{2}, \frac{1}{2}), (1,1)$ :

\begin{array}{l} l_{0} = \frac{(X + \frac{1}{2}) \cdot (X - 0) \cdot (X - \frac{1}{2}) \cdot (X - 1)}{(- 1 + \frac{1}{2}) \cdot (- 1 - 0) \cdot (- 1 - \frac{1}{2}) \cdot (- 1 - 1)} = \frac{2}{3} (X^{4} - X^{3} - \frac{1}{4} X^{2} + \frac{1}{4} X) \\ l_{1} = \frac{(X + 1) \cdot (X - 0) \cdot (X - \frac{1}{2}) \cdot (X - 1)}{(- \frac{1}{2} + 1) \cdot (- \frac{1}{2} - 0) \cdot (- \frac{1}{2} - \frac{1}{2}) \cdot (- \frac{1}{2} - 1)} = - \frac{8}{3} (X^{4} - \frac{1}{2} X^{3} - X^{2} + \frac{1}{2} X) \\ l_{2} = \frac{(X + 1) \cdot (X + \frac{1}{2}) \cdot (X - \frac{1}{2}) \cdot (X - 1)}{(0 + 1) \cdot (0 + \frac{1}{2}) \cdot (0 - \frac{1}{2}) \cdot (0 - 1)} = 4 (X^{4} - \frac{5}{4} X^{2} + \frac{1}{4}) \\ l_{3} = \frac{(X + 1) \cdot (X + \frac{1}{2}) \cdot (X - 0) \cdot (X - 1)}{(\frac{1}{2} + 1) \cdot (\frac{1}{2} + \frac{1}{2}) \cdot (\frac{1}{2} - 0) \cdot (\frac{1}{2} - 1)} = - \frac{8}{3} (X^{4} + \frac{1}{2} X^{3} - X^{2} - \frac{1}{2} X) \\ l_{4} = \frac{(X + 1) \cdot (X + \frac{1}{2}) \cdot (X - 0) \cdot (X - \frac{1}{2})}{(1 + 1) \cdot (1 + \frac{1}{2}) \cdot (1 - 0) \cdot (1 - \frac{1}{2})} = \frac{2}{3} (X^{4} + X^{3} - \frac{1}{4} X^{2} - \frac{1}{4} X) \end{array}

Damit berechnet sich das zweite Interpolationspolynom (für fünf Stützpunkte) zu:

p_{5} = l_{0} + \frac{1}{2} l_{1} + 0 l_{2} + \frac{1}{2} l_{3} + l_{4} = - \frac{4}{3} X^{4} + \frac{7}{3} X^{2}

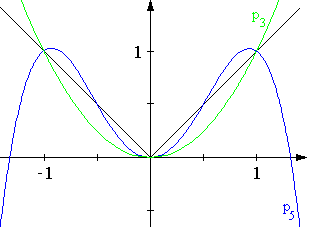
In der folgenden Skizze sind beide Interpolationspolynome und die Betragsfunktion eingezeichnet. Einerseits erkennt man deutlich, dass $p_{5}$ sich besser an die Betragsfunktion anschmiegt als $p_{3}$ , andererseits wird aber auch klar, dass außerhalb von [-1,1] beide Interpolationspolynome nur noch sehr wenig mit $| X |$ zu tun haben. Verbesserungen ergeben sich vielleicht, wenn man die Zahl der Stützpunkte erhöht oder ihren Bereich ausweitet. Dies aber sind Fragestellungen aus dem Bereich der Numerik. Dort entwickelt man auch andere Interpolationsverfahren, die auf komplexere Aufgabenstellungen bessere Antworten geben können.

Hier stellen wir jetzt eine Variante des Lagrange-Verfahrens vor, die sog. baryzentrische Form. Bei einem gegebenen Satz von Stützstellen $x_{0}, \dots, x_{n}$ setzen wir dazu für $k = 0, \dots, n$ die Stützkoeffizienten (auch: baryzentrischen Gewichte) fest durch

λ_{k}^{(n)} ≔ \prod_{\begin{matrix} i = 0 \\ i \neq k \end{matrix}}^{n} \frac{1}{x_{k} - x_{i}}

[4.0.8]

Spielt die Anzahl der Stützstellen keine Rolle, so schreiben wir nur $λ_{k}$ . Für das Interpolationspolynom p erhält man damit die Darstellung

p = \sum_{k = 0}^{n} y_{k} λ_{k} \prod_{\begin{matrix} i = 0 \\ i \neq k \end{matrix}}^{n} (X - x_{i})

[4.0.9]

Stellt man p in der Standardform $p = a_{n} X^{n} + \dots + a_{0}$ dar, so ist $\sum_{k = 0}^{n} y_{k} λ_{k}$ gerade der Koeffizient von $X^{n}$ . Und da für $y_{k} = 1$ p das konstante Polynom 1 ist, hat man so für jedes $n > 0$ die Gleichheit

\sum_{k = 0}^{n} λ_{k} = 0

[4.0.10]

gesichert. Als weitere Abkürzung setzen wir für $x \neq x_{k}$

μ_{k}^{(n)} (x) ≔ \frac{λ_{k}^{(n)}}{x - x_{k}}

[4.0.11]

Auch hier verkürzen wir zu $μ_{k} (x)$ , wenn der Bezug zu n nicht wichtig ist. Beachtet man, dass

λ_{k} \prod_{\begin{matrix} i = 0 \\ i \neq k \end{matrix}}^{n} (x - x_{i}) = \frac{λ_{k}}{x - x_{k}} \prod_{i = 0}^{n} (x - x_{i})

so haben wir außerhalb der Stützstellen, also für $x \notin {x_{0}, \dots, x_{n}}$ :

p (x) = \sum_{k = 0}^{n} y_{k} λ_{k} \prod_{\begin{matrix} i = 0 \\ i \neq k \end{matrix}}^{n} (x - x_{i}) = \prod_{i = 0}^{n} (x - x_{i}) \sum_{k = 0}^{n} y_{k} μ_{k} (x)

[4.0.12]

Das ist die 1. baryzentrische Form des Lagrangeschen Interpolationspolynoms. Wählt man auch hier $y_{k} = 1$ , also $p (x) = 1$ , so erhält man $\prod_{i = 0}^{n} (x - x_{i}) = \frac{1}{\sum_{k = 0}^{n} μ_{k} (x)}$ , und damit die 2. baryzentrische Form:

p (x) = \frac{\sum_{k = 0}^{n} y_{k} μ_{k} (x)}{\sum_{k = 0}^{n} μ_{k} (x)}

[4.0.13]

Die baryzentrische Form erweist sich als vorteilhaft, wenn man einen bereits gegebenen Satz von Stützpunkten $(x_{0}, y_{0}), \dots, (x_{n}, y_{n})$ durch einen weiteren Punkt $(x_{n + 1}, y_{n + 1})$ ergänzen will. Während bei der Lagrange-Darstellung alle Grundpolynome neu berechnet werden müssten, gewinnt man die hier notwendigen neuen Stützkoeffizienten leicht aus den alten:

\begin{array}{l} λ_{k}^{(n + 1)} = \frac{λ_{k}^{(n)}}{x_{k} - x_{n + 1}} & für k \leq n \\ λ_{n + 1}^{(n + 1)} = - \sum_{k = 0}^{n} λ_{k}^{(n + 1)} & gemäß [4.0.10] \end{array}

[4.0.14]

Wir zeigen dies mit einem Beispiel für die 1. baryzentrische Form

und nehmen dazu noch einmal die Stützpunkte aus dem ersten Beispiel, also (2 , 4) , (6 , 6) . Mit
$\begin{array}{l} λ_{0} = λ_{0}^{(1)} = \frac{1}{2 - 6} = - \frac{1}{4} & μ_{0} (x) = \frac{λ_{0}}{x - 2} = \frac{- \frac{1}{4}}{x - 2} \\ λ_{1} = λ_{1}^{(1)} = \frac{1}{6 - 2} = \frac{1}{4} & μ_{1} (x) = \frac{λ_{1}}{x - 6} = \frac{\frac{1}{4}}{x - 6} \end{array}$
ist dann
$p (x) = (x - 2) \cdot (x - 6) \cdot (- \frac{1}{x - 2} + \frac{\frac{3}{2}}{x - 6}) = - (x - 6) + \frac{3}{2} (x - 2) = \frac{1}{2} x + 3$ .
Wir fügen (3 , 0) als weiteren Stützpunkt hinzu und berechnen die neuen Daten gemäß [4.0.14]:
$\begin{array}{l} λ_{0}^{(2)} = \frac{λ_{0}^{(1)}}{2 - 3} = \frac{1}{4} & μ_{0} (x) = \frac{\frac{1}{4}}{x - 2} \\ λ_{1}^{(2)} = \frac{λ_{1}^{(1)}}{6 - 3} = \frac{1}{12} & μ_{1} (x) = \frac{\frac{1}{12}}{x - 6} \\ λ_{2}^{(2)} = - (\frac{1}{4} + \frac{1}{12}) = - \frac{1}{3} & μ_{2} (x) = \frac{- \frac{1}{3}}{x - 3} \end{array}$
$\begin{array}{l} Also: p (x) & = (x - 2) \cdot (x - 6) \cdot (x - 3) \cdot (\frac{1}{x - 2} + \frac{\frac{1}{2}}{x - 6} + \frac{0}{x - 3}) \\ = (x - 6) \cdot (x - 3) + \frac{1}{2} (x - 2) \cdot (x - 3) \\ = \frac{3}{2} x^{2} - \frac{23}{2} x + 21 . \end{array}$