Ein physikalisches Beispiel: Schwingungen
1. Ungedämpfte Schwingungen
Ein Massenpunkt der Masse ist durch eine (massenlose) Feder an eine Ruhelage gebunden. Entfernt man diesen Punkt in Federrichtung um s Einheiten aus seiner Ruhelage,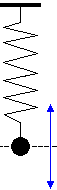 so stellt sich eine rücktreibende Kraft F ein. Im einfachsten Fall erfüllt sie das Hookesche Gesetz, d.h. F ist direkt proportional zu s: so stellt sich eine rücktreibende Kraft F ein. Im einfachsten Fall erfüllt sie das Hookesche Gesetz, d.h. F ist direkt proportional zu s:
Der Proportionalitätsfaktor ist dabei die Federkonstante. Ihr Wert hängt von der geometrischen Form, von den Abmessungen und vom Material der Feder ab. Beachte: D bezeichnet in diesem Beispiel nicht die Diskriminante einer quadratischen Gleichung!
Läßt man den Massenpunkt los, so wird er auf Grund des Newtonschen Aktionsprinzips in Richtung der Ruhelage beschleunigt und somit zu einer (eindimensionalen) Bewegung gezwungen. Unterstellt man nun, dass keine weiteren Kräfte auf den Massenpunkt wirken, so ergibt sich die Bewegungsgleichung (in physikalischer Notation) dabei aus der zu jedem Zeitpunkt t bestehenden Gleichheit
Geht man davon aus, dass zum Zeitpunkt der Massenpunkt um Einheiten aus der Ruhelage entfernt ist, d.h. und noch keine Bewegung ausführt, die Anfangsgeschwindigkeit also den Wert 0 hat, d.h. , so ist die Zeit-Weg-Funktion des Punktes offenbar die eindeutige Lösung der Differentialgleichung (in mathematischer Notation)
unter der Anfangsbedingung und .
Das zugehörige Polynom hat keine Lösung. Mit den Daten und erhält man daher unter der Anfangsbedingung die Lösung nach [8.12.7]:
,
in physikalischer Schreibweise also: . Damit haben wir die Bewegungsgleichung einer ungedämpften Schwingung hergeleitet. Mit ihr sind weitere Kenndaten der Schwingung gegeben:
-
Der Betrag der Anfangsentfernung ist die Amplitude der Schwingung. Der Massenpunkt wird sich niemals weiter als von der Ruhelage entfernen.
-
Die Frequenz der Schwingung, also die Anzahl der cos-Perioden pro Zeiteinheit, ergibt sich zu .
-
Die Schwingungsdauer T gibt die Anzahl der Zeiteinheiten an, die für eine cos-Periode benötigt wird. Sie ist der Kehrwert der Frequenz: .
Das folgende Applet simuliert die ungedämpfte Schwingung eines Massenpunktes der Masse m = 1 kg. Die Auslenkung lässt sich über einen Schieber auf Werte zwischen −1 m und 1 m einstellen, die Federkonstante D zwischen 0 N/m und 100 N/m.
2. Gedämpfte Schwingungen
Wir befreien uns nun von der sehr idealisierten Voraussetzung, der Massenpunkt unterliege keinen weiteren Kräften. In aller Regel nämlich werden - etwa durch eine innere Reibung im Federmaterial - Reibungskräfte auftreten. Häufig ist eine solche Reibungskraft R der Geschwindigkeit proportional und ihr stets entgegen gerichtet:
,
Die Bewegungsgleichung muss also modifiziert werden:
Wir betrachten also jetzt unter der Anfangsbedingung und die Differentialgleichung
.
Je nach Vorzeichen der Diskriminante sind nun drei Fälle zu unterscheiden. Die Anfangsbedingung und bleibt unverändert.
-
: Das zugehörige Polynom hat also zwei verschiedene Nullstellen
Die Lösung ergibt sich daher nach [8.12.5] zu
-
: Mit als doppelter Lösung errechnet man hier mit [8.12.6]:
-
: Mit und ergibt sich jetzt die Lösung aus [8.12.7]:
Bei einer gedämpften Schwingung liegt nur im dritten Fall eine periodische Lösungsfunktion vor, denn nur hier treten überhaupt sin- und cos-Anteile auf.
Mit der Frequenz ist auch die Schwingungsdauer gegeben. Man beachte zudem, dass der Faktor hier eine zeitabhängige Amplitude erzwingt. Da , weiß man sogar: , eine gedämpfte Schwingung kommt also langfristig zum Stillstand.
Das folgende Applet enthält einen zusätzlichen Schieber für die Reibungskonstante k. Um den beschriebenen Stillstand gut beobachten zu können, sollte man für k einen kleinen Wert einstellen..
3. Erzwungene Schwingungen
Greift nun an dem schwingenden Massenpunkt eine zusätzliche, sog. äußere Kraft an, so spricht man von einer erzwungenen Schwingung. In der Regel ist dies eine periodische wirkende Kraft der Form
,
wobei über den Speziallfall auch konstant wirkende Kräfte mit einbezogen sind. Die Bewegungsgleichung ändert sich dadurch zu:
.
Es ist also unter der Anfangsbedingung die inhomogene Differentialgleichung
zu lösen. Nach [8.12.16-18] ist dazu die Summe des Faltungsprodukts und der bereits gefundenen Lösung f der gedämpften Schwingung zu ermitteln (Zur Erinnerung: ist die Lösung der homogenen Gleichung unter der Anfangsbedingung ). Die Ermittlung dieses Faltungsprodukts ist aber - vor allem im dritten Fall - außerordentlich aufwändig, eine computergestütze Hilfe (wie etwa der bereits erwähnte Integrator von Mathematica) ist daher sehr willkommen.
Wir nehmen also noch einmal die drei Fälle des letzten Abschnitts auf und notieren dabei der Reihe nach gemäß [8.12.11], und schließlich die Lösung in physikalischer Notation. Mit den Daten für die gedämpften Schwingungen erhalten wir dabei:
-
:
Mit [1] erhält man in diesem Fall also die Lösung
-
:
Nach [2] erhält man als Lösung jetzt
-
:
Aus Bequemlichkeit notieren wir die Lösung hier nur in ihrer abgekürzten Form. Dabei haben wir [3] benutzt.
Erzwungene Schwingungen sind äußerst komplexe Prozesse. Bei ihren Lösungsfunktionen lassen sich daher auch nur wenige allgemeine Tendenzen beobachten:
-
Ist die äußere Kraft konstant, etwa als Resultat der Erdbeschleunigung, so wird lediglich die Nulllage der Schwingung verschoben.
-
Störfrequenzen, die nahe bei der Eigenfrequenz liegen, führen zu einem unbegrenzten Amplitudenwachstum. In realen Situationen kommt es dabei zu einer Zerstörung des Systems (Resonanzkatastrophe).
-
Eine zusätzliche Dämpfung führt in der Regel nach einer Einschwingphase zu stabilen Verhältnissen. Frequenzbestimmend ist dabei die Störfrequenz.
Im unserem letzen Applet lassen sich nun auch die Größe F der äußeren Kraft und ihre Störfrequenz variieren. Die gerade beschriebenen Verhältnisse können durch geeignete Schieberstellungen überprüft werden.
|  so stellt sich eine rücktreibende Kraft F ein. Im einfachsten Fall erfüllt sie das
so stellt sich eine rücktreibende Kraft F ein. Im einfachsten Fall erfüllt sie das