8.12. Lineare Differentialgleichungen 2. Ordnung

Differentialgleichungen der Ordnung 2 enthalten neben der ersten auch noch die zweite Ableitung der Unbekannten f. Während wir auch für Gleichungen 2. Ordnung eine Lösungsformel entwicklen können, ist dies bei Gleichungen höherer Ordnung i.A. nicht mehr möglich. Allerdings werden die dort eingesetzten Strategien bereits in diesem Abschnitt angesprochen.

Definition: Ist

g : ℝ \to ℝ

eine Funktion und

p, q \in ℝ

, so nennen wir die Gleichung

f^{''} + p f^{'} + q f = g

[8.12.1]

eine (normierte) lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten (über $ℝ$ ).

Unter einer Lösung dieser Gleichung verstehen wir eine auf $ℝ$ zweimal differenzierbare Funktion f, also $f \in D^{2} (ℝ)$ , die die Gleichung [8.12.1] erfüllt.

Ist speziell die rechte Seite $g = 0$ , so nennt man die Gleichung [8.12.1] homogen.

Bei den Differentialgleichungen erster Ordnung haben wir auch mit Begriffen aus der linearen Algebra gearbeitet. Diese Notation nehmen wir hier wieder auf und erklären den zum Polynom

r ≔ X^{2} + p X + q

gehörigen Differentialoperator $D_{r} : D^{2} (ℝ) \to F (ℝ)$ durch die Festsetzung

D_{r} (f) ≔ f^{''} + p f^{'} + q f

$D_{r}$ ein linearer Operator, d.h.

\begin{array}{l} D_{r} (f + g) = D_{r} (f) + D_{r} (g) \\ D_{r} (α f) = α D_{r} (f) \end{array}

[0]

und die Lösungsmenge der homogenen Gleichung $D_{r} (f) = 0$ ist $K e r D_{r} (f)$ , der Kern des Operators $D_{r}$ .

Der in [8.11] ermittelte Kern $K e r D_{X + a} = < e^{- a X} >$ ist das Erzeugnis der Funktion $e^{- a X}$ , die durch die Nullstelle des Polynoms $X + a$ charakterisiert ist. Interessanterweise setzt sich dieses Prinzip hier fort. Die Nullstellensuche führt bei unserem Polynom r allerdings auf die quadratische Gleichung $x^{2} + p x + q = 0$ , deren Lösungsverhaltung vom Vorzeichen ihrer Diskrimnante

D ≔ \frac{p^{2}}{4} - q

abhängt. In diesem Abschnitt unterscheiden wir daher drei Fälle:

$D > 0$ , d.h. r hat zwei verschiedene Nullstellen $c_{0}$ und $c_{1}$ . Sie erfüllen nach dem Satz von Viëta die Gleichungen

$- (c_{0} + c_{1}) = p$ und $c_{0} \cdot c_{1} = q$ .
$D = 0$ , d.h. r hat eine doppelte Nullstelle c. Gemäß Viëta hat man hier

$- 2 c = p$ und $c^{2} = q$ .
$D < 0$ . Zwar hat in diesem Fall r keine reelle Nullstelle, aber mit den Abkürzungen $u ≔ - \frac{p}{2}$ und $v ≔ \sqrt{- D}$ hat man jetzt

$- 2 u = p$ und $u^{2} + v^{2} = q$ .

Für die folgenden Überlegungen legen wir das oben eingeführte Polynom r und die gerade gesetzten Daten $c_{0}, c_{1}, c, u, v$ sowie D zu Grunde.

Wir beginnen mit der Untersuchung homogener Gleichungen. Die folgende Bemerkung gibt bereits eine vollständige Übersicht über ihr Lösungsverhalten.

Bemerkung: Für jede $D^{2}$ -Funktion f gilt:

f^{''} + p f^{'} + q f = 0

$\Leftrightarrow {\begin{array}{l} f = \frac{f^{'} (0) - c_{1} f (0)}{c_{0} - c_{1}} e^{c_{0} X} + \frac{f^{'} (0) - c_{0} f (0)}{c_{1} - c_{0}} e^{c_{1} X}, falls D > 0 \\ f = f (0) e^{c X} + (f^{'} (0) - c f (0)) X e^{c X}, falls D = 0 \\ f = \frac{f^{'} (0) - f (0)}{v} \sin (v X) e^{u X} + f (0) \cos (v X) e^{u X}, falls D < 0 \end{array}$	[8.12.2]
	[8.12.3]
	[8.12.4]

Beweis: In allen drei Fällen gelingt es, die Richtung " $\Rightarrow$ " mit einer Verfeinerung der Beweismethode aus [8.11.2] nachzuweisen. Sei also f eine $D^{2}$ -Funktion mit $f^{''} + p f^{'} + q f = 0$ .

1. ► Wir berechnen zunächst die Ableitung der differenzierbaren Funktion $\frac{f^{'} - c_{1} f}{e^{c_{0} X}}$ :
i

Man beachte dabei: $- (c_{0} + c_{1}) = p$ und $c_{0} \cdot c_{1} = q$ .

(\frac{f^{'} - c_{1} f}{e^{c_{0} X}})^{'} = \frac{f^{''} - c_{1} f^{'} - c_{0} (f^{'} - c_{1} f)}{e^{c_{0} X}} = \frac{f^{''} - (c_{0} + c_{1}) f^{'} + c_{0} \cdot c_{1} f}{e^{c_{0} X}} = 0

Gemäß Mittelwertsatz ist die abgeleitete Funktion also konstant. Man hat daher für ein geeignetes $k_{0}$ :

f^{'} - c_{1} f = k_{0} e^{c_{0} X}

Analog findet man ein $k_{1}$ , so dass

f^{'} - c_{0} f = k_{1} e^{c_{1} X}

Durch Subtrahieren dieser beiden Gleichungen erhält man die Darstellung

(c_{0} - c_{1}) f = k_{0} e^{c_{0} X} - k_{1} e^{c_{1} X}

[1]

und zusammen mit der Ableitung $(c_{0} - c_{1}) f^{'} = k_{0} c_{0} e^{c_{0} X} - k_{1} c_{1} e^{c_{1} X}$ das lineare Gleichungssystem

\begin{array}{l} (c_{0} - c_{1}) f (0) & = k_{0} - k_{1} & \underset{c_{1} I - I I}{\Leftrightarrow} & (c_{0} - c_{1}) (c_{1} f (0) - f^{'} (0)) & = (c_{1} - c_{0}) k_{0} \\ (c_{0} - c_{1}) f^{'} (0) & = c_{0} k_{0} - c_{1} k_{1} & (c_{0} - c_{1}) f (0) & = k_{0} - k_{1} \end{array}

Mit seiner Lösung $\begin{array}{l} k_{0} & = f^{'} (0) - c_{1} f (0) \\ k_{1} & = k_{0} - (c_{0} - c_{1}) f (0) = f^{'} (0) - c_{0} f (0) \end{array}$ folgt nun [8.12.2] aus [1].

2. ► Wie in 1. finden wir zunächst ein k, so dass

f^{'} - c f = k e^{c X}

.[2]

Die Ableitung der differenzierbaren Funktion $\frac{f^{'} - (c - 1) f}{e^{c X}}$
i

Man beachte hier: $- 2 c = p$ und $c^{2} = q$ .

\begin{array}{l} (\frac{f^{'} - (c - 1) f}{e^{c X}})^{'} & = \frac{f^{''} - (c - 1) f^{'} - c (f^{'} - (c - 1) f)}{e^{c X}} \\ = \frac{f^{''} - 2 c f + c^{2} f + f^{'} - c f}{e^{c X}} \\ = \frac{0 + k e^{c X}}{e^{c X}} = k \end{array}

ist konstant, die Funktion selbst somit linear. Für ein geeignetes l hat man daher

f^{'} - (c - 1) f = (k X + l) e^{c X}

Wir subtrahieren die Gleichung [2] und erhalten so direkt die Darstellung

f = (l - k) e^{c X} + k X e^{c X}

.[3]

Beachtet man auch noch die Ableitung $f^{'} = c (l - k) e^{c X} + k (1 + c X) e^{c X}$ , so gewinnt man jetzt das Gleichungssystem

\begin{array}{l} f (0) & = l - k & \underset{I I - c I}{\Leftrightarrow} & f^{'} (0) - c f (0) & = k \\ f^{'} (0) & = c (l - k) + k & f (0) & = l - k \end{array}

Dies aber sichert mit [3] die Gleichung [8.12.3].

3. ► Wir betrachten jetzt die $D^{1}$ -Funktion $\frac{f^{'} \cdot \cos (v X) - f \cdot (u \cos (v X) - v \sin (v X))}{e^{u X}}$ . Ihre Ableitung errechnen
i

Zur Erinnerung: $- 2 u = p$ und $u^{2} + v^{2} = q$ .

wir zu

\begin{array}{l} \frac{1}{e^{u X}} & (f^{''} \cdot \cos (v X) - f^{'} \cdot v \sin (v X) \\ - f^{'} \cdot (u \cos (v X) - v \sin (v X)) + f \cdot (u v \sin (v X) + v^{2} \cos (v X)) \\ - u f^{'} \cdot \cos (v X) + u f \cdot (u \cos (v X) - v \sin (v X))) \\ = & \frac{1}{e^{u X}} & (f^{''} - 2 u f^{'} + (u^{2} + v^{2}) f) \cos (v X) = 0 \end{array}

Es gibt daher ein $k_{0}$ , so dass

f^{'} \cdot \cos (v X) - f \cdot (u \cos (v X) - v \sin (v X)) = k_{0} e^{u X}

.[4]

Eine analoge Rechnung führt zu

f^{'} \cdot \sin (v X) - f \cdot (u \sin (v X) + v \cos (v X)) = k_{1} e^{u X}

[5]

mit einem geeigneten $k_{1}$ . Mit $\sin^{2} + \cos^{2} = 1$ (Satz des Pythagoras) ergibt sich nun aus der Differenz $[4] \cdot \sin (v X) - [5] \cdot \cos (v X)$ die Darstellung

v f = k_{0} \sin (v X) e^{u X} - k_{1} \cos (v X) e^{u X}

[6]

und damit die Ableitung $v f^{'} = k_{0} (v \cos (v X) + u \sin (v X)) e^{u X} - k_{1} (- v \sin (v X) + u \cos (v X)) e^{u X}$ .

Über das Gleichungssystem

\begin{array}{l} v f (0) & = - k_{1} & \Leftrightarrow & - k_{1} & = v f (0) \\ v f^{'} (0) & = v k_{0} - u k_{1} & k_{0} & = f' (0) + \frac{u k_{1}}{v} = f^{'} (0) - u f (0) \end{array}

schließlich ergibt sich aus [6] die Darstellung [8.12.4].

Für die Richtung " $\Leftarrow$ " zeigen wir jetzt, dass die Funktionen in [8.12.2,3,4] die Differentialgleichung $f^{''} + p f^{'} + q f = 0$ erfüllen. Auf Grund der Linearität des Operators $D_{r}$ (siehe [0]) genügt es dabei, dies für die vier "Erzeugerfunktionen" $e^{c X}$ , $X e^{c X}$ , $\sin (v X) e^{u X}$ und $\cos (v X) e^{u X}$ zu zeigen.

1. ► Ist c eine beliebige Lösung der Gleichung $x^{2} + p x + q = 0$ , also $c^{2} + p c + q = 0$ , so ist

(e^{c X})^{''} + p (e^{c X})^{'} + q e^{c X} = (c^{2} + p c + q) e^{c X} = 0

2. ► Sei c jetzt eine doppelte Lösung. Neben $c^{2} + p c + q = 0$ beachten wir auch $2 c + p = 0$ . Mit

\begin{array}{l} (X e^{c X})^{'} & = e^{c X} + c X e^{c X} = (1 + c X) e^{c X} \\ (X e^{c X})^{''} & = c e^{c X} + c (1 + c X) e^{c X} = (2 c + c^{2} X) e^{c X} \end{array}

hat man daher:

\begin{array}{l} (X e^{c X})^{''} + p (X e^{c X})^{'} + q X e^{c X} & = (2 c + c^{2} X + p (1 + c X) + q X) e^{c X} \\ = (2 c + p + (c^{2} + p c + q) X) e^{c X} = 0 \end{array}

3. ► Mit den Beziehungen $p = - 2 u$ , $q = u^{2} + v^{2}$ und den Ableitungen

\begin{array}{l} (\sin (v X) e^{u X})^{'} & = (v \cos (v X) + u \sin (v X)) e^{u X} \\ (\sin (v X) e^{u X})^{''} & = (- v^{2} \sin (v X) + u v \cos (v X) + u v \cos (v X) + u^{2} \sin (v X)) e^{u X} \\ = (2 u v \cos (v X) + (u^{2} - v^{2}) \sin (v X)) e^{u X} \end{array}

errechnet man in diesem Fall:

\begin{array}{l} (\sin (v X) e^{u X})^{''} + p (\sin (v X) e^{u X})^{'} + q \sin (v X) e^{u X} \\ = & (2 u v \cos (v X) + (u^{2} - v^{2}) \sin (v X) + p v \cos (v X) + p u \sin (v X) + q \sin (v X)) e^{u X} \\ = & ((2 u + p) v \cos (v X) + (\underset{= 2 u^{2} - 2 u^{2}}{\underset{︸}{u^{2} - v^{2} + p u + q}}) \sin (v X)) e^{u X} = 0 \end{array}

4. ► Der Nachweis für $\cos (v X) e^{u X}$ ist eine direkte Analogie zu 3.

Beachte:

Nach [8.12.2-4] besteht die Lösungsmenge der Gleichung $f^{''} + p f^{'} + q f = 0$ aus allen Linearkombinationen der jeweiligen Erzeugerfunktionen:

f^{''} + p f^{'} + q f = 0 \Leftrightarrow f \in K e r D_{r} = {\begin{array}{l} < e^{c_{0} X}, e^{c_{1} X} >,  falls D > 0 \\ < e^{c X}, X e^{c X} >,  falls D = 0 \\ < \sin (v X) e^{u X}, \cos (v X) e^{u X} >,  falls D < 0 \end{array}

Also ist die Lösungsmenge wieder ein Untervektorraum, diesmal von $D^{2} (ℝ)$ , und zwar ein Untervektorraum der Dimension 2.
i

Wir weisen in allen drei Fällen nach, dass die jeweilige Erzeugersequenz linear unabhängig ist:

1. ► Mit $f = α e^{c_{0} X} + β e^{c_{1} X} = 0$ , ist auch $f^{'} = 0$ und damit insbesondere: $f (0) = f^{'} (0) = 0$ . Also hat man das Gleichungssystem

$\begin{array}{r} α + β & = 0 \\ c_{0} α + c_{1} β & = 0 \end{array}$ ,

das wegen $c_{0} \neq c_{1}$ nur die Lösung $α = β = 0$ zuläßt.

2. ► Ist $f = α e^{c X} + β X e^{c X} = 0$ , so ergibt sich sofort $α = f (0) = 0$ , und damit auch $β e^{c} = f (1) = 0$ , also: $β = 0$ .

3. ► Sei schließlich $f = α \sin (v X) e^{u X} + β \cos (v X) e^{u X} = 0$ . Man errechnet sofort: $β = f (0) = 0$ und $α e^{π u / 2 v} = f (\frac{π}{2 v}) = 0$ , also auch $α = 0$ .

[8.12.2-4] macht auch deutlich, dass wir eine eindeutige Lösung nur dann erhalten können, wenn wir für $f (0)$ und für $f^{'} (0)$ eine Anfangsbedingung setzen.

Bemerkung: Für je zwei Zahlen $w_{0}, w_{1} \in ℝ$ hat die homogene Gleichung $f^{''} + p f^{'} + q f = 0$ unter der Anfangsbedingung $f (0) = w_{0}$ und $f^{'} (0) = w_{1}$ genau eine Lösung:

f^{''} + p f^{'} + q f = 0 \land f (0) = w_{0} \land f^{'} (0) = w_{1}

$\Leftrightarrow {\begin{array}{l} f = \frac{w_{1} - w_{0} c_{1}}{c_{0} - c_{1}} e^{c_{0} X} + \frac{w_{1} - w_{0} c_{0}}{c_{1} - c_{0}} e^{c_{1} X}, falls D > 0 \\ f = w_{0} e^{c X} + (w_{1} - c w_{0}) X e^{c X}, falls D = 0 \\ f = \frac{w_{1} - w_{0} u}{v} \sin (v X) e^{u X} + w_{0} \cos (v X) e^{u X}, falls D < 0 \end{array}$	[8.12.5]
	[8.12.6]
	[8.12.7]

Beweis: In allen drei Fällen folgt die Richtung " $\Rightarrow$ " direkt aus [8.12.2-4]. " $\Leftarrow$ " folgt ebenfalls mit [8.12.2-4], weil:

1. ► $f (0) = \frac{w_{1} - w_{0} c_{1} - w_{1} + w_{0} c_{0}}{c_{0} - c_{1}} = w_{0}$ ,
1. ► $f^{'} (0) = \frac{(w_{1} - w_{0} c_{1}) c_{0} + (- w_{1} + w_{0} c_{0}) c_{1}}{c_{0} - c_{1}} = w_{1}$ .

2. ► $f (0) = w_{0}$ und $f^{'} (0) = w_{0} c + w_{1} - c w_{0} = w_{1}$ .

3. ► $f (0) = w_{0}$ und $f^{'} (0) = w_{1} - w_{0} u + w_{0} u = w_{1}$ .

Bei der Formulierung der Anfangsbedingung ist man nicht an die Stelle 0 gebunden, denn für alle $b, w_{0}, w_{1} \in ℝ$ gilt:

f^{''} + p f^{'} + q f = 0 \land f (b) = w_{0} \land f^{'} (b) = w_{1}

$\Leftrightarrow {\begin{array}{l} f = \frac{w_{1} - w_{0} c_{1}}{c_{0} - c_{1}} e^{c_{0} (X - b)} + \frac{w_{1} - w_{0} c_{0}}{c_{1} - c_{0}} e^{c_{1} (X - b)}, falls D > 0 \\ f = (w_{0} - b (w_{1} - c w_{0})) e^{c (X - b)} + (w_{1} - c w_{0}) X e^{c (X - b)}, falls D = 0 \\ f = \frac{w_{1} - w_{0} u}{v} \sin (v (X - b)) e^{u (X - b)} + w_{0} \cos (v (X - b)) e^{u (X - b)}, falls D < 0 \end{array}$
[8.12.8]

[8.12.9]

[8.12.10]

Beweis: Wir orientieren uns am Beweis von [8.11.4]. Da

\begin{array}{l} f^{''} + p f^{'} + q f = 0 \land f (b) = w_{0} \land f^{'} (b) = w_{1} \\ \Leftrightarrow & (f \circ (X + b))^{''} + p (f \circ (X + b))^{'} + q f \circ (X + b) = 0 \\ \land f \circ (X + b) (0) = w_{0} \land (f \circ (X + b))^{'} (0) = w_{1} \end{array}

ist $f \circ (X + b)$ die Lösungsfunktion aus [8.12.5-7]:

f \circ (X + b) = {\begin{array}{l} \frac{w_{1} - w_{0} c_{1}}{c_{0} - c_{1}} e^{c_{0} X} + \frac{w_{1} - w_{0} c_{0}}{c_{1} - c_{0}} e^{c_{1} X},  falls D > 0 \\ w_{0} e^{c X} + (w_{1} - c w_{0}) X e^{c X},  falls D = 0 \\ \frac{w_{1} - w_{0} u}{v} \sin (v X) e^{u X} + w_{0} \cos (v X) e^{u X},  falls D < 0 \end{array}

Das ist aber bereits die Behauptung, wenn man die Identität $f = f \circ (X + b) \circ (X - b)$ berücksichtigt.

Beispiel:

Die Lösungsmenge der Gleichung $f^{''} + f^{'} - 6 f = 0$ ist das Erzeugnis $< e^{2 X}, e^{- 3 X} >$ , denn das Polynom $X^{2} + X - 6$ hat die beiden verschiedenen Nullstellen 2 und −3 (Fall $D > 0$ ). Daher hat man z.B.:

$\begin{array}{l} f^{''} + f^{'} - 6 f = 0 \land f (0) = 2 \land f^{'} (0) = 3 \\ \Leftrightarrow & f = \frac{9}{5} e^{2 X} + \frac{1}{5} e^{- 3 X} \end{array}$
Das Polynom $X^{2} - 8 X + 16$ hat die doppelte Lösung 4 (Fall $D = 0$ ). Der Kern des Operators $D_{X^{2} - 8 X + 16}$ ist also das Erzeugnis $< e^{4 X}, X e^{4 X} >$ . Somit hat man etwa:

$\begin{array}{l} f^{''} - 8 f^{'} + 16 = 0 \land f (0) = - 2 \land f^{'} (0) = 1 \\ \Leftrightarrow & f = - 2 e^{4 X} + 9 X e^{4 X} \end{array}$
Das Polynom $X^{2} + 4$ hat keine reelle Lösung (Fall $D < 0$ ), so dass jetzt die Daten $u = - \frac{p}{2} = 0$ und $v = \sqrt{- D} = 2$ ermittelt werden müssen. Mit ihnen erhält man die Erzeugerfunktionen $\sin (2 X)$ und $\cos (2 X)$ und damit z.B.:

$\begin{array}{l} f^{''} + 4 f = 0 \land f (0) = 0 \land f^{'} (0) = 6 \\ \Leftrightarrow & f = 3 \sin (2 X) \end{array}$

Das Lösen homogener Gleichungen 2. Grades ist leicht zu automatisieren. Man kann also eine Fülle weiterer Beispiele selbst herstellen. Dazu trägt man zunächst in der nachstehenden Tabelle die Parameter p und q ein und legt die Anfangswerte $f (b)$ und $f^{'} (b)$ für die Stelle b fest:

$p =$		$q =$
$f (b) =$		$f^{'} (b) =$		$b =$

Per Klick erhält man nun die Lösung: solve ►. Um die Darstellung übersichtlich zu halten, werden dabei die Koeffizienten auf 3 Stellen gerundet.

\begin{array}{l} f^{''} ​ ​ ​^{​} ​ ​ ​ = 0 \land f (​ 0) = ​ 0 \land f^{'} (​ 0) = ​ 0 \\ \Leftrightarrow & f = ​ 0 ​ ​ ​ ​ ​ ​ ​ ​ ​ ​^{​ ​ ​ ​ ​ ​ ​} ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​^{​ ​ ​ ​ ​ ​ ​} \end{array}

In einem Anwendungsbeispiel zur Physik leiten wir verschiedene Schwingungsgleichungen her.

Wir wenden uns nun den inhomogenen Gleichungen zu. Wie bereits im letzten Abschnitt ist auch hier das Faltungsprodukt der eigentliche Schlüssel, der die Lösbarkeit bei stetiger rechter Seite g garantiert.

Im Folgenden bezeichne $f_{\circ}$ die Lösung der homogenen Gleichung $f^{''} + p f^{'} + q f = 0$ unter der speziellen Anfangsbedingung $f (0) = 0$ und $f^{'} (0) = 1$ . Wir setzen also gemäß [8.12.5-7] fest:

$f_{\circ} ≔ {\begin{array}{l} \frac{1}{c_{0} - c_{1}} e^{c_{0} X} + \frac{1}{c_{1} - c_{0}} e^{c_{1} X}, falls D > 0 \\ X e^{c X}, falls D = 0 \\ \frac{1}{v} \sin (v X) e^{u X}, falls D < 0 \end{array}$
[8.12.11]

und haben damit: ${f_{\circ}}^{''} + p {f_{\circ}}^{'} + q f_{\circ} = 0$ mit $f_{\circ} (0) = 0$ und ${f_{\circ}}^{'} (0) = 1$ . Über das Faltungsprodukt gewinnen wir nun aus der $C^{\infty}$ -Funktion $f_{\circ}$ eine spezielle Lösung der inhomogenen Gleichung.

Bemerkung: Ist $g : ℝ \to ℝ$ eine stetige Funktion, so löst das Faltungsprodukt $f_{\circ} * g$ die Gleichung $f^{''} + p f^{'} + q f = g$ unter der Anfangsbedingung $f (0) = 0$ und $f^{'} (0) = 0$ :

(f_{\circ} * g)^{''} + p (f_{\circ} * g)^{'} + q (f_{\circ} * g) = g \land f_{\circ} * g (0) = 0 \land (f_{\circ} * g)^{'} (0) = 0

[8.12.12]

Beweis: Man beachte zunächst, dass $f_{\circ}$ stetig, das Faltungsprodukt also wohldefiniert ist. Nun ist gemäß [8.10.10] die Funktion $f_{\circ} * g$ zweimal differenzierbar und

\begin{array}{l} (f_{\circ} * g)^{'} & = f_{\circ} (0) \cdot g + {f_{\circ}}^{'} * g = {f_{\circ}}^{'} * g \\ (f_{\circ} * g)^{''} & = f_{\circ}' (0) \cdot g + {f_{\circ}}^{''} * g = g + {f_{\circ}}^{''} * g \end{array}

Mit den Rechenregeln [8.10.5,6,3] erhalten wir also:

\begin{array}{l} (f_{\circ} * g)^{''} + p (f_{\circ} * g)^{'} + q (f_{\circ} * g) & = g + {f_{\circ}}^{''} * g + p ({f_{\circ}}^{'} * g) + q (f_{\circ} * g) \\ = g + ({f_{\circ}}^{''} + p {f_{\circ}}^{'} + q f_{\circ}) * g \\ = g + 0 * g = g \end{array}

Schließlich hat man auf Grund von [8.10.2]: $f_{\circ} * g (0) = 0$ und $(f_{\circ} * g)^{'} (0) = {f_{\circ}}^{'} * g (0) = 0$ .

Mit [8.12.12] gelingt es nun, die Lösungsmenge einer inhomogenen Gleichung (mit einer stetigen rechten Seite) zu beschreiben.

Bemerkung: Sei $g \in C^{0} (ℝ)$ . Dann gilt für jede $D^{2}$ -Funktion f:

f^{''} + p f^{'} + q f = g

$\Leftrightarrow f = f_{\circ} * g + {\begin{array}{l} \frac{f^{'} (0) - c_{1} f (0)}{c_{0} - c_{1}} e^{c_{0} X} + \frac{f^{'} (0) - c_{0} f (0)}{c_{1} - c_{0}} e^{c_{1} X}, falls D > 0 \\ f (0) e^{c X} + (f^{'} (0) - c f (0)) X e^{c X}, falls D = 0 \\ \frac{f^{'} (0) - f (0)}{v} \sin (v X) e^{u X} + f (0) \cos (v X) e^{u X}, falls D < 0 \end{array}$	[8.12.13]
	[8.12.14]
	[8.12.15]

Beweis: Beachtet man, dass $f - f_{\circ} * g (0) = f (0)$ und $(f - f_{\circ} * g)^{'} (0) = f^{'} (0)$ , so ergibt sich die Behauptung direkt aus [8.12.2-4], denn mit [8.12.12] hat man:

\begin{array}{l} f^{''} + p f^{'} + q f = g \\ \Leftrightarrow & f^{''} + p f^{'} + q f = (f_{\circ} * g)^{''} + p (f_{\circ} * g)^{'} + q (f_{\circ} * g) \\ \Leftrightarrow & (f - f_{\circ} * g)^{''} + p (f - f_{\circ} * g)^{'} + q (f - f_{\circ} * g) = 0 \end{array}

Beachte:

Wie bereits im letzten Abschnitt gewinnen wir auch jetzt alle Lösungen der inhomogenen Gleichung indem wir zu einer speziellen Lösung alle Lösungen der zugehörigen homogenen Gleichung addieren. Die Lösungsmenge ist somit der 2-dimensionale affine Unterraum

$f_{\circ} * g + K e r D_{r}$

von $D^{2} (ℝ)$ .

Erwartungsgemäß garantiert [8.12.13-15] nun die eindeutige Lösbarkeit einer inhomogenen Gleichung mit Anfangsbedingung.

Bemerkung: Es sei $g \in C^{0} (ℝ)$ , $w_{0}, w_{1} \in ℝ$ . Dann hat die inhomogene Gleichung $f^{''} + p f^{'} + q f = g$ unter der Anfangsbedingung $f (0) = w_{0}$ und $f^{'} (0) = w_{1}$ genau eine Lösung:

f^{''} + p f^{'} + q f = g \land f (0) = w_{0} \land f^{'} (0) = w_{1}

$\Leftrightarrow f = f_{\circ} * g + {\begin{array}{l} \frac{w_{1} - w_{0} c_{1}}{c_{0} - c_{1}} e^{c_{0} X} + \frac{w_{1} - w_{0} c_{0}}{c_{1} - c_{0}} e^{c_{1} X}, falls D > 0 \\ w_{0} e^{c X} + (w_{1} - c w_{0}) X e^{c X}, falls D = 0 \\ \frac{w_{1} - w_{0} u}{v} \sin (v X) e^{u X} + w_{0} \cos (v X) e^{u X}, falls D < 0 \end{array}$	[8.12.16]
	[8.12.17]
	[8.12.18]

Beweis: Der Nachweis wiederholt nur noch einmal die Argumente im Beweis von [8.12.5-7]. Man beachte dabei, dass $f_{\circ} * g (0) = 0$ und $(f_{\circ} * g)^{'} (0) = 0$ .

Nach [8.12.16-18] konstruieren wir die Lösung einer inhomogenen Gleichung in drei Schritten (wobei die oben notierte Lösungshilfe
i

für homogene Gleichungen sehr nützlich sein kann!):

Finde die Lösung $f_{\circ}$ der homogenen Gleichung unter der Anfangsbedingung $f (0) = 0$ und $f^{'} (0) = 1$ .
Berechne das Faltungsprodukt $f_{\circ} * g$ .
Addiere dazu die Lösung der homogenen Gleichung unter der Anfangsbedingung $f (0) = w_{0}$ und $f^{'} (0) = w_{1}$ .

Um nun auch bei inhomogenen Gleichungen die Anfangsbedingung auf einen beliebigen Punkt b legen zu können, gehen wir analog zum Beweis von [8.12.8-10] vor: Zunächst finden wir eine Lösung f der Gleichung

f^{''} + p f^{'} + q f = g \circ (X + b) \land f (0) = w_{0} \land f^{'} (0) = w_{1}

und haben dann mit $f \circ (X - b)$ die ursprüngliche Aufgabe gelöst. Wir zeigen dieses Verfahren in den Beispielen und verzichten hier auf eine explizite Darstellung.

Beispiel:

$f^{''} + 2 f^{'} - 3 f = e^{X} \land f (0) = 2 \land f^{'} (0) = - 1$

Das Polynom $X^{2} + 2 X - 3$ hat zwei verschiedene Nullstellen, nämlich 1 und −3. Wir ermitteln die Lösung f in drei Schritten:

$f_{\circ} = \frac{1}{4} e^{X} - \frac{1}{4} e^{- 3 X}$ nach [8.12.11]

$f_{\circ} * e^{X} = \frac{1}{4} X e^{X} - \frac{1}{16} e^{X} + \frac{1}{16} e^{- 3 X}$ Berechnung anzeigen ►
i

$\begin{array}{l} f_{\circ} * e^{X} (x) & = \frac{1}{4} \int_{0}^{x} (e^{x - X} - e^{- 3 (x - X)}) e^{X} \\ = \frac{1}{4} (e^{x} \int_{0}^{x} 1 - e^{- 3 x} \int_{0}^{x} e^{4 X}) \\ = \frac{1}{4} (x e^{x} - e^{- 3 x} \frac{1}{4} (e^{4 x} - 1)) \\ = \frac{1}{4} x e^{x} - \frac{1}{16} e^{x} + \frac{1}{16} e^{- 3 x} \end{array}$

$f = f_{\circ} * e^{X} + \underset{nach [8.12.16]}{\underset{︸}{\frac{5}{4} e^{X} + \frac{3}{4} e^{- 3 X}}} = \frac{1}{4} X e^{X} + \frac{19}{16} e^{X} + \frac{13}{16} e^{- 3 X}$

$f^{''} + 16 f = \cos (4 X) \land f (0) = \frac{1}{2} \land f^{'} (0) = - 2$

$X^{2} + 16$ hat keine reelle Nullstelle, so dass wir auf die Daten $u = 0$ und $v = 4$ zurückgreifen müssen. Wir errechnen die Lösung f wieder in drei Schritten:

$f_{\circ} = \frac{1}{4} \sin (4 X)$

$f_{\circ} * \cos (4 X) = \frac{1}{32} \sin (4 X) \cdot 4 X$ Berechnung anzeigen ►
i

Wir benötigen das Additionstheorem für die Sinusfunktion:

$\sin (x - y) = \sin x \cdot \cos y - \cos x \cdot \sin y$

und die Stammfunktionen $\frac{1}{2} (\sin \cdot \cos + X)$ zu $\cos^{2}$ (siehe [8.3]) bzw. $\frac{1}{2} \sin^{2}$ zu $\sin \cdot \cos$ (Typ $f \cdot f^{'}$ !). Damit errechnen wir:

$\begin{array}{l} f_{\circ} * \cos (4 X) (x) & = \frac{1}{4} \int_{0}^{x} \sin (4 x - 4 X) \cdot \cos (4 X) \\ = \frac{1}{4} \int_{0}^{x} (\sin (4 x) \cdot \cos (4 X) - \cos (4 x) \cdot \sin (4 X)) \cdot \cos (4 X) \\ = \frac{\sin (4 x)}{4} \int_{0}^{x} \cos^{2} (4 X) - \frac{\cos (4 x)}{4} \int_{0}^{x} \sin (4 X) \cdot \cos (4 X) \\ = \frac{\sin (4 x)}{4} \cdot \frac{1}{8} (\sin (4 X) \cdot \cos (4 X) + 4 X) |_{0}^{x} - \frac{\cos (4 x)}{4} \cdot \frac{1}{8} \sin^{2} (4 X) |_{0}^{x} \\ = \frac{1}{32} \sin (4 x) (\sin (4 x) \cdot \cos (4 x) + 4 x - \cos (4 x) \cdot \sin (4 x)) \\ = \frac{1}{32} \sin (4 x) \cdot 4 x \end{array}$

$f = f_{\circ} * \cos (4 X) \underset{gemäß [8.12.18]}{\underset{︸}{- \frac{1}{2} \sin (4 X) + \frac{1}{2} \cos (4 X)}} = \frac{1}{2} (\sin (4 X) \cdot (\frac{1}{4} X - 1) + \cos (4 X))$

$f^{''} + 2 f^{'} + f = X \land f (4) = - 2 \land f^{'} (4) = 3$

Da die Anfangsbedingung für die Stelle 4 formuliert ist, lösen wir zunächst die Gleichung

f^{''} + 2 f^{'} + f = X \circ (X + 4) = X + 4 \land f (0) = - 2 \land f^{'} (0) = 3

Dazu berechnen wir wieder der Reihe nach (−1 ist doppelte Nullstelle von $X^{2} + 2 X + 1$ ):

$f_{\circ} = X e^{- X}$

$f_{\circ} * (X + 4) = - (2 + 3 X) e^{- X} + X + 2$ Berechnung anzeigen ►
i

Wir integrieren zweimal partiell:

$\begin{array}{l} f_{\circ} * (X + 4) (x) & = \int_{0}^{x} (x - X) e^{- (x - X)} \cdot (X + 4) \\ = e^{- x} \int_{0}^{x} (- X^{2} + (x - 4) X + 4 x) e^{X} \\ = e^{- x} ((- X^{2} + (x - 4) X + 4 x) e^{X} |_{0}^{x} + \int_{0}^{x} (2 X - x + 4) e^{X}) \\ = e^{- x} (- 4 x + (2 X - x + 4) e^{X} |_{0}^{x} - 2 \int_{0}^{x} e^{X}) \\ = e^{- x} (- 4 x + (x + 4) e^{x} + x - 4 - 2 e^{x} + 2) \\ = e^{- x} (- 2 - 3 x) + (x + 2) e^{x}) \\ = - (2 + 3 x) e^{- x} + x + 2 \end{array}$

$f = f_{\circ} * (X + 4) \underset{siehe [8.12.17]}{\underset{︸}{- 2 e^{- X} + X e^{- X}}} = - (4 + 2 X) e^{- X} + X + 2$

Schließlich erhält mit $f \circ (X - 4) = (4 - 2 X) e^{- X + 4} + X - 2$ die gesuchte Lösung.

Analog zum Regularitätsverhalten der Gleichungen 1. Ordnung, erweisen sich die Lösungen f unserer Gleichungen jetzt um zwei Differenzierbarkeitsklassen besser als die rechte Seite g.

Bemerkung: Ist f eine Lösung der Gleichung $f^{''} + p f^{'} + q f = g$ , so gilt für jedes $n \in ℕ^{*}$ :

$g \in D^{n} (ℝ) \Rightarrow f \in D^{n + 2} (ℝ)$	[8.12.19]
$g \in C^{n} (ℝ) \Rightarrow f \in C^{n + 2} (ℝ)$	[8.12.20]
$g \in C^{\infty} (ℝ) \Rightarrow f \in C^{\infty} (ℝ)$	[8.12.21]

Beweis: 3. ist eine direkte Folgerung aus 1. Die Aussagen 1. und 2. beweisen wir simultan per Induktion und beachten dabei die Gleichung

f^{''} = g - p f^{'} - q f

[+]

" $n = 1$ ": Als Lösung der Gleichung $f^{''} + p f^{'} + q f = g$ ist f zweimal differenzierbar. Ist nun g eine $D^{1}$ -Funktion, so trifft dies nach [+] auch auf $f^{''}$ zu. f ist damit eine $D^{3}$ -Funktion mit

$f^{'''} = g^{'} - p f^{''} - q f^{'}$ ,

also auch eine $C^{3}$ -Funktion falls $g^{'}$ stetig ist.
" $n \Rightarrow n + 1$ ": Sei jetzt g eine $D^{n + 1} / C^{n + 1}$ -Funktion, also erst recht eine $D^{n} / C^{n}$ -Funktion. Nach Induktionsvoraussetzung ist f dann $(n + 2)$ -mal (stetig) differenzierbar, wobei nach [+]

$f^{(n + 2)} = g^{(n)} - p f^{(n + 1)} - q f^{(n)}$ .

Da $g^{(n)}$ eine $D^{1} / C^{1}$ -Funktion ist, folgt somit: f ist $(n + 3)$ -mal (stetig) differenzierbar.

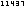8.11. 8.13.