mathproject >> 8.3. Partielle Integration und Substitutionsregel

Satz (Regel der partiellen Integration): f und g seien zwei differenzierbare Funktionen auf I, also

f, g \in D^{1} (I)

. Dann gilt:

Ist $f^{'} \cdot g$ auf I integrierbar, so gilt dies auch für $f \cdot g^{'}$ . Dabei hat man für alle $a, b \in I$ :

\int_{a}^{b} f \cdot g^{'} = f \cdot g |_{a}^{b} - \int_{a}^{b} f^{'} \cdot g

[8.3.1]

Beweis: Zunächst ist die Funktion $f \cdot g$ gemäß Produktregel [7.7.6] differenzierbar mit $(f \cdot g)^{'} = f^{'} \cdot g + f \cdot g^{'}$ . Also besitzt $f^{'} \cdot g + f \cdot g^{'}$ eine Stammfunktion, und zwar $f \cdot g$ . Mit $f^{'} \cdot g$ ist daher nach [8.1.7] auch $f \cdot g^{'} = f^{'} \cdot g + f \cdot g^{'} - f^{'} \cdot g$ integrierbar und aus der Gleichheit

\int_{a}^{b} f^{'} \cdot g + \int_{a}^{b} f \cdot g^{'} = \int_{a}^{b} f^{'} \cdot g + f \cdot g^{'} = f \cdot g |_{a}^{b}

folgt sofort die Formel [8.3.1].

Der bei weitem wichtigste Anwendungsbereich der partiellen Integration ist das Errechnen von Stammfunktionen über den Hauptsatz [8.2.13]. Wir demonstrieren diese Technik an einigen Beispielen.

Beispiel:

$- X \cdot \cos + \sin$ ist eine Stammfunktion zu $X \cdot \sin$ , denn für alle $x \in ℝ$ ist

$\begin{array}{l} \int_{0}^{x} X \cdot \sin & = \int_{0}^{x} X \cdot (- \cos)^{'} \\ = X \cdot (- \cos) |_{0}^{x} - \int_{0}^{x} X^{'} \cdot (- \cos) \\ = - X \cdot \cos |_{0}^{x} + \int_{0}^{x} \cos \\ = - X \cdot \cos |_{0}^{x} + \sin |_{0}^{x} \\ = - x \cdot \cos x + \sin x \end{array}$
$- X^{2} \cdot \cos + 2 X \cdot \sin + 2 \cos$ ist eine Stammfunktion zu $X^{2} \cdot \sin$ : Wir integrieren zweimal partiell und erhalten so für alle $x \in ℝ$

$\begin{array}{l} \int_{0}^{x} X^{2} \cdot \sin & = \int_{0}^{x} X^{2} \cdot (- \cos)^{'} \\ = X^{2} \cdot (- \cos) |_{0}^{x} + \int_{0}^{x} 2 X \cdot \cos \\ = - X^{2} \cdot \cos |_{0}^{x} + \int_{0}^{x} 2 X \cdot \sin^{'} \\ = - X^{2} \cdot \cos |_{0}^{x} + 2 X \cdot \sin |_{0}^{x} - \int_{0}^{x} 2 \cdot \sin \\ = - X^{2} \cdot \cos |_{0}^{x} + 2 X \cdot \sin |_{0}^{x} + 2 \cos |_{0}^{x} \\ = - x^{2} \cdot \cos x + 2 x \cdot \sin x + 2 \cos x - 2 \end{array}$

und damit zunächst $- X^{2} \cdot \cos + 2 X \cdot \sin + 2 \cos - 2$ als eine Stammfunktion zu $X^{2} \cdot \sin$ . Den konstanten Summanden −2 lassen wir anschließend weg.
Im letzten Beispiel errechnen wir eine Stammfunktion zu $\cos^{2}$ . Die Rechnung benutzt den Satz des Pythagoras (hier in der Form $\sin^{2} = 1 - \cos^{2}$ ), ein Standardtrick!

Zunächst haben wir für $x \in ℝ$ :

$\begin{array}{l} \int_{0}^{x} \cos^{2} = \int_{0}^{x} \cos \cdot \cos & = \int_{0}^{x} \cos \cdot \sin^{'} \\ = \cos \cdot \sin |_{0}^{x} - \int_{0}^{x} \cos^{'} \cdot \sin \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} \sin^{2} \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} 1 - \cos^{2} \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} 1 - \int_{0}^{x} \cos^{2} \end{array}$

Damit ist das gesuchte Integral zwar noch nicht ermittelt, aber es erfüllt eine Gleichung, die wir zu

$\int_{0}^{x} \cos^{2} = \frac{1}{2} (\sin \cdot \cos |_{0}^{x} + \int_{0}^{x} 1) = \frac{1}{2} (\sin x \cdot \cos x + x)$

lösen können, so dass wir schließlich $\frac{1}{2} (\sin \cdot \cos + X)$ als eine Stammfunktion zu $\cos^{2}$ erhalten.

Der Satz des Pythagoras wird bei der partiellen Integration oft eingesetzt. Wir zeigen diesen Standardtrick noch einmal bei den Rekursionsformeln für die Integrale über $\sin^{n}$ und $\cos^{n}$ .

Bemerkung: Für alle $a, b \in ℝ$ und alle $n \geq 2$ ist

$\int_{a}^{b} \sin^{n} = - \frac{\cos \cdot \sin^{n - 1}}{n} \|_{a}^{b} + \frac{n - 1}{n} \int_{a}^{b} \sin^{n - 2}$	[8.3.2]
$\int_{a}^{b} \cos^{n} = \frac{\sin \cdot \cos^{n - 1}}{n} \|_{a}^{b} + \frac{n - 1}{n} \int_{a}^{b} \cos^{n - 2}$	[8.3.3]

Beweis: Beide Nachweise verlaufen analog. Wir führen daher nur einen, beispielhaft etwa den zu 2. Mit $\sin^{2} = 1 - \cos^{2}$ erhalten wir die folgende Gleichung für $\int_{a}^{b} \cos^{n}$ :

\begin{array}{l} \int_{a}^{b} \cos^{n} = \int_{a}^{b} \sin^{'} \cdot \cos^{n - 1} & = \sin \cdot \cos^{n - 1} |_{a}^{b} - \int_{a}^{b} \sin \cdot (n - 1) \cos^{n - 2} \cdot (- \sin) \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \sin^{2} \cdot \cos^{n - 2} \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} (1 - \cos^{2}) \cdot \cos^{n - 2} \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \cos^{n - 2} - (n - 1) \int_{a}^{b} \cos^{n} \end{array}

Damit haben wir: $n \int_{a}^{b} \cos^{n} = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \cos^{n - 2}$ , also im Prinzip die Behauptung.

Sind a und b Nullstellen der Sinus- oder Cosinusfunktion, so lassen sich diese Rekursionsformeln vereinfachen zu

\int_{a}^{b} \sin^{n} = \frac{n - 1}{n} \int_{a}^{b} \sin^{n - 2}

und

\int_{a}^{b} \cos^{n} = \frac{n - 1}{n} \int_{a}^{b} \cos^{n - 2}

In solchen Fällen ist es leichter, eine rekursionsfreie Darstellung zu finden. Das folgende Integral benötigen wir in [8.5.7] zur Berechnung des Kugelvolumens.

Bemerkung: Für alle $n \geq 0$ ist

\int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} = {\begin{array}{l} \frac{n!}{{(2^{k} k!)}^{2}} \cdot π falls n = 2 k \\ \frac{{(2^{k} k!)}^{2}}{n!} \cdot 2 falls n = 2 k + 1 \end{array}

[8.3.4]

Beweis: Für $k = 0$ ist das Integral in beiden Fällen elementar auszuwerten. O.E. sei also $k > 0$ . Ist $n = 2 k$ , so läßt sich die verkürzte Rekusionsformel genau k mal anwenden:

\begin{array}{l} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} & = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{1}{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{0} \\ = \frac{n (n - 1)}{n^{2}} \cdot \frac{(n - 2) (n - 3)}{{(n - 2)}^{2}} \cdot \dots \cdot \frac{2 \cdot 1}{2^{2}} \cdot π \\ = \frac{n!}{{((2 k) \cdot (2 k - 2) \cdot \dots \cdot (2 k - 2 (k - 1)))}^{2}} \cdot π \\ = \frac{n!}{(2^{k} {(k \cdot (k - 1) \cdot \dots \cdot (k - (k - 1)))}^{2}} \cdot π & (2 k mal ausklammern) \\ = \frac{n!}{{(2^{k} k!)}^{2}} \cdot π \end{array}

Im Fall $n = 2 k + 1$ gehen wir analog vor. Auch hier wenden wir die kurze Rekursionsformel k mal an:

\begin{array}{l} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} & = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{2}{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{1} \\ = \frac{{(n - 1)}^{2}}{n \cdot (n - 1)} \cdot \frac{{(n - 3)}^{2}}{(n - 2) \cdot (n - 3)} \cdot \dots \cdot \frac{2^{2}}{3 \cdot 2} \cdot 2 \\ = \frac{{((2 k) \cdot (2 k - 2) \cdot \dots \cdot (2 k - 2 (k - 1)))}^{2}}{n!} \cdot 2 \\ = \frac{(2^{k} {(k \cdot (k - 1) \cdot \dots \cdot (k - (k - 1)))}^{2}}{n!} \cdot 2 \\ = \frac{{(2^{k} k!)}^{2}}{n!} \cdot 2 \end{array}

Wir übertragen nun die Kettenregel in ihre Integralversion. Anders als bei der partiellen Integration greift die Substitutionsregel auch auf die Integrationsgrenzen zu.

Satz (Substitutionsregel): I und J seien zwei Intervalle und $g : J \to I$ eine differenzierbare Funktion. Ist f integrierbar auf I, d.h. $f \in I (I)$ , so ist $(f \circ g) \cdot g^{'} \in I (J)$ und für alle $a, b \in J$ gilt

\int_{a}^{b} (f \circ g) \cdot g^{'} = \int_{g (a)}^{g (b)} f

[8.3.5]

Beweis: Sei h eine Stammfunktion zu f. Nach Kettenregel ([7.7.8]) ist $h \circ g$ differenzierbar auf I mit

(h \circ g)^{'} = (h^{'} \circ g) \cdot g^{'} = (f \circ g) \cdot g^{'}

$(f \circ g) \cdot g^{'}$ besitzt also in $h \circ g$ eine Stammfunktion und

\int_{a}^{b} (f \circ g) \cdot g^{'} = (h \circ g) |_{a}^{b} = h |_{g (a)}^{g (b)} = \int_{g (a)}^{g (b)} f

Beachte:

Insbesondere bei der Anwendung der Substitutionsregel ist die dx-Schreibweise weit verbreitet. Dazu muss allerdings neben dx, dem Differential der Identität, auch das Differential

d g (x) = g^{'} (x) \cdot d x

einer beliebigen differenzierbaren Funktion g betrachtet werden.

Substituiert man nun $t = g (x)$ , also $d t = g^{'} (x) d x$ , so garantiert die Substitutionsregel, dass die durch bloßes Austauschen gewonnene Gleichung

\int_{a}^{b} f (g (x)) \cdot g^{'} (x) d x = \int_{g (a)}^{g (b)} f (t) d t

auch gültig ist. Die folgenden Beispiele zeigen meist beide Schreibformen der Substitutionsregel. Über die Schaltflächen ◄ und ► lassen sie sich jeweils ein- und ausblenden.

Die Substitutionsregel läßt sich sowohl von links nach rechts wie auch von rechts nach links lesen und anwenden. Die erste Lesart setzt man ein, wenn der Integrand erkennbar die Form $(f \circ g) \cdot g^{'}$ hat, die Substitution g also direkt abgelesen werden kann.

Im zweiten Fall muss man eigenständig eine Substitution g so einführen, dass das Integral über $(f \circ g) \cdot g^{'}$ leichter zu errechnen ist als das über f. Dabei ist auch zu berücksichtigen, dass man jetzt g-Urbilder der Integrationsgrenzen finden muss. Für ein bijektives g gelingt dies über die Umkehrfunktion, so dass [8.3.5] für $a, b \in I$ umformuliert werden kann zu

$\int_{a}^{b} f = \int_{g^{- 1} (a)}^{g^{- 1} (b)} (f \circ g) \cdot g^{'}$

Die beiden ersten Beispiele üben die Substitutionsregel in der Richtung von links nach rechts.

Beispiel: Wir berechnen das Integral $\int_{0}^{1} (X^{2} + 1)^{4} \cdot 2 X = \int_{0}^{1} (x^{2} + 1)^{4} \cdot 2 x d x$ mit der Substitution

◄►

$g = X^{2} + 1, g^{'} = 2 X$

\begin{array}{l} \int_{0}^{1} (X^{2} + 1)^{4} \cdot 2 X \\ = & \int_{0}^{1} X^{4} \circ (X^{2} + 1) \cdot (X^{2} + 1)^{'} \\ = & \int_{1}^{2} X^{4} \\ = & \frac{1}{5} X^{5} |_{1}^{2} = \frac{31}{5} \end{array}

$t = x^{2} + 1, d t = 2 x d x$

\begin{array}{l} \int_{0}^{1} (x^{2} + 1)^{4} \cdot 2 x d x \\ = & \int_{1}^{2} t^{4} d t \\ = & \frac{1}{5} t^{5} |_{1}^{2} = \frac{31}{5} \end{array}

Beim folgenden Beispiel machen wir uns den zunächst fehlenden Faktor 3 durch einen Standardtrick, hier $1 = \frac{1}{3} \cdot 3$ , verfügbar. Da konstante Faktoren stets vor das Integral gezogen werden können, ist ein nicht passender Faktor grundsätzlich kein Hindernis.

Beispiel: Für das Integral $\int_{0}^{2} \frac{X^{2}}{2 \sqrt{X^{3} + 1}} = \int_{0}^{2} \frac{x^{2}}{2 \sqrt{x^{3} + 1}} d x$ verwenden wir die Substitution

◄►

$g = X^{3} + 1, g^{'} = 3 X^{2}$

\begin{array}{l} \int_{0}^{2} \frac{X^{2}}{2 \sqrt{X^{3} + 1}} \\ = & \frac{1}{3} \int_{0}^{2} \frac{3 X^{2}}{2 \sqrt{X^{3} + 1}} \\ = & \frac{1}{3} \int_{0}^{2} \frac{1}{2 \sqrt{X}} \circ (X^{3} + 1) \cdot (X^{3} + 1)^{'} \\ = & \frac{1}{3} \int_{1}^{9} \frac{1}{2 \sqrt{X}} \\ = & \frac{1}{3} \sqrt{X} |_{1}^{9} = \frac{2}{3} \end{array}

$t = x^{3} + 1, d t = 3 x^{2} d x$

\begin{array}{l} \int_{0}^{2} \frac{x^{2}}{2 \sqrt{x^{3} + 1}} d x \\ = & \frac{1}{3} \int_{0}^{2} \frac{1}{2 \sqrt{x^{3} + 1}} \cdot 3 x^{2} d x \\ = & \frac{1}{3} \int_{1}^{9} \frac{1}{2 \sqrt{t}} d t \\ = & \frac{1}{3} \sqrt{t} |_{1}^{9} = \frac{2}{3} \end{array}

Im nächsten Beispiel wenden wir die Substitutionsregel von rechts nach links an. Da der Integrand jetzt nicht die Form $(f \circ g) \cdot g^{'}$ hat, ergibt sich die Substitution g nicht "von selbst". Ohne Erfahrung wirken manche Substitionen zunächst willkürlich und fremd.

In unserem Beispiel wählen wir als Substitution die Sinusfunktion. Motiviert ist diese Wahl durch die Bauart des Integranden und die Hoffnung, anschließend den Satz des Pythagoras $\sin^{2} + \cos^{2} = 1$ erfolgreich einbringen zu können. Man beachte ferner, dass wir in einem vorherigen Beispiel $\frac{1}{2} (\sin \cdot \cos + X)$ bereits als eine Stammfunktion zu $\cos^{2}$ nachgewiesen haben.

Beispiel: Das Integral $\int_{- 1}^{1} \sqrt{1 - X^{2}} = \int_{- 1}^{1} \sqrt{1 - x^{2}} d x$ lösen wir mit der Substitution

◄►

$g = \sin, g^{'} = \cos$

\begin{array}{l} \int_{- 1}^{1} \sqrt{1 - X^{2}} \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - X^{2}} \circ \sin \cdot \sin^{'} \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - \sin^{2}} \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{\cos^{2}} \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} | \cos | \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} = \frac{1}{2} (\sin \cdot \cos + X) |_{- \frac{π}{2}}^{\frac{π}{2}} = \frac{π}{2} \end{array}

$x = \sin t, d x = \cos t d t$

\begin{array}{l} \int_{- 1}^{1} \sqrt{1 - x^{2}} d x \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - \sin^{2} t} \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{\cos^{2} t} \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} | \cos t | \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} t d t \\ = & \frac{1}{2} (\sin t \cdot \cos t + t) |_{- \frac{π}{2}}^{\frac{π}{2}} = \frac{π}{2} \end{array}

In einem letzten Beispiel berechnen wir mit Hilfe der Substitutionsregel (und zwar in beiden Richtungen) für ein beliebiges $r > 0$ eine Stammfunktion zu

\sqrt{1 - \frac{X^{2}}{r^{2}}} : [- r, r] \to ℝ

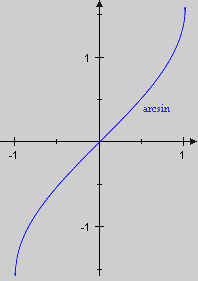
Die Ähnlichkeit mit dem letzten Beispiel wird wieder eine Substitution mit der Sinusfunktion nahe legen. Allerdings sind jetzt die Integrationsgrenzen variabel, so dass wir die Umkehrbarkeit von g benötigen. sin selbst ist nicht bijektiv, wohl aber die Einschränkung $\sin | [- \frac{π}{2}, \frac{π}{2}]$ . Sie besitzt in

\arcsin = {(\sin | [- \frac{π}{2}, \frac{π}{2}])}^{- 1} : [- 1, 1] \to [- \frac{π}{2}, \frac{π}{2}]

eine Umkehrfunktion, den Arcussinus. Dieses Beispiel rechnen wir nur in der dx-Schreibweise vor.

Beispiel: Da cos auf dem Bild $\arcsin ([- 1, 1]) = [- \frac{π}{2}, \frac{π}{2}]$ positiv und $\frac{1}{2} (\sin \cdot \cos + X)$ als eine Stammfunktion zu $\cos^{2}$ bekannt ist, erhalten wir (wieder mit dem Satz des Pythagoras) zunächst für ein beliebiges $x \in [- r, r]$ :

\begin{array}{l} \int_{- r}^{x} \sqrt{1 - \frac{u^{2}}{r^{2}}} d u & = r \int_{- r}^{x} \sqrt{1 - \frac{u^{2}}{r^{2}}} \cdot \frac{1}{r} d u \\ = r \int_{- 1}^{\frac{x}{r}} \sqrt{1 - t^{2}} d t Substitution t = \frac{u}{r}, d t = \frac{1}{r} d u \\ = r \int_{\arcsin (- 1)}^{\arcsin \frac{x}{r}} \sqrt{1 - \sin^{2} z} \cdot \cos z d z Substitution t = \sin z, d t = \cos z d z \\ = r \int_{\arcsin (- 1)}^{\arcsin \frac{x}{r}} \cos^{2} z d z \\ = \frac{r}{2} (\sin z \cdot \cos z + z) |_{- \frac{π}{2}}^{\arcsin \frac{x}{r}} \\ = \frac{r}{2} (\frac{x}{r} \cdot \cos (\arcsin \frac{x}{r}) + \arcsin \frac{x}{r} + \frac{π}{2}) \end{array}

Damit haben wir eine Stammfunktion zu $\sqrt{1 - \frac{X^{2}}{r^{2}}}$ errechnet, nämlich:

\frac{X}{2} \cdot \cos (\arcsin \frac{X}{r}) + \frac{r}{2} \cdot \arcsin \frac{X}{r} = \frac{X}{2} \cdot \sqrt{1 - \frac{X^{2}}{r^{2}}} + \frac{r}{2} \cdot \arcsin \frac{X}{r}

Mit der Substitutiosregel zeigt man leicht, dass Integrale verschiebungsunabhängig sind.

Bemerkung: Sei f integrierbar über I und $a, b \in I$ . Dann ist für ein beliebiges $c \in ℝ$

\int_{a}^{b} f = \int_{a + c}^{b + c} f \circ (X - c)

[8.3.6]

Beweis: Da $(X - c)^{'} = 1$ kann man die Substitutionsregel anwenden und erhält

\int_{a + c}^{b + c} f \circ (X - c) = \int_{X - c (a + c)}^{X - c (b + c)} f = \int_{a}^{b} f

8.2. 8.4.