8.5. Volumenberechnung
In diesem Abschnitt soll ein allgemeines Konzept zur Volumenberechnung entwickelt werden mit dem Ziel, geeigneten Teilmengen M des eine Maßzahl zuzuweisen, die im zweidimensionalen Fall mit den alten Flächenmaßzahlen und im dreidimensionalen Fall mit den Volumenvorstellungen übereinstimmt.
Wir werden dies, angelehnt an die Interpretation des Flächenmaßes am Ende des letzten Abschnitts, rekursiv gestalten: Das (n + 1)-dimensionale Volumen einer Menge M wird durch Aufintegrieren der n-dimensionalen Volumina ihrer Schnitte gewonnen.
|
Definition: Ist eine Teilmenge des , so nennen wir für jedes die Menge
|
[8.5.1] |
einen Schnitt in M.
|
Das folgende Applet visualisiert für den Schnitt in einem Zuckerhut (display by
JavaView
i  |
|
JavaView ist ein interaktiver Betrachter für 3-dimensionale Geometrien. Mit der linken Maustaste läßt sich die Darstellung steuern, z.B.
Alle Möglichkeiten sind hier aufgelistet: www.javaview.de/jars/shortcuts.html. Mit der rechten Maustaste läßt sich ein umfangreiches Kontextmenü aufrufen.
|
).
Wir berechnen zur Übung einige Schnitte in überschaubaren Teilmengen des und des . In Beispielen auftretende Parameter seien stets positiv.
|
Beispiel:
-
Die Schnitte in einem Quadrat sind (konstante) Intervalle, denn für ist
|
[1] |
-
Die Schnitte in einer Ellipse sind (variable) Intervalle, den für ist
|
[2] |
Man beachte den Fall : ist hier das einpunktige Intervall .
-
Die Schnitte in einer Lochscheibe sind aufwändiger zu berechnen. Für ist nämlich
|
[3] |
Im Sonderfall sind die Schnitte in L ein- bzw. zweipunktig:
-
Die Schnitte in einem Würfel sind (konstante) Quadrate, denn für ist
|
[4] |
-
Die Schnitte in einer Kugel (Sphäre)
sind Kreise (mit variablem Radius), denn für ist
|
[5] |
Im speziellen Fall ist ein Kreis mit Radius 0, also ein Punkt.
|
Wir setzen nun rekursiv fest, wann eine Menge M zur Volumenberechnung geeignet sein soll, und welches Volumen ihr dann zukommt. Wir orientieren uns dabei an der zum Ende des vorherigen Abschnitts betrachteten Interpretation der Flächenmaßzahlen.
|
Definition:
-
Ist eine disjunkte Vereinigung

i  |
|
Die Vereinigung zweier Mengen A und B heißt disjunkt (elementfremd) falls . In diesem Fall ersetzt man das Zeichen oft durch das Symbol .
Ein Download der Schrift Lucida Bright Math Symbol löst Probleme bei der Darstellung.
|
endlich vieler abgeschlossener Intervalle, , so sagen wir: M besitzt das eindimensionale Volumen
|
[8.5.2] |
Zusätzlich setzen wir .
-
Ist , , so sagen wir: M besitzt ein ()-dimensionales Volumen, falls für jedes der Schnitt ein n-dimensionales Volumen besitzt und die Funktion über integrierbar ist. In diesem Fall heißt die Zahl
|
[8.5.3] |
das ()-dimensionale Volumen von M. Ist , so setzen wir zusätzlich .
|
Beachte:
-
Durch eine kleine induktive Überlegung erweisen sich Volumina als positive Zahlen: .
-
Aufgrund der jeweiligen Zusätze haben alle endlichen Mengen das Volumen Null:
-
[8.5.2] enthält auch den (häufigen) Sonderfall . M ist dann ein Intervall, , , und das Volumen verkürzt sich zu .
-
Mit [8.5.3] haben wir das Prinzip des Cavalieri etabliert:
seien zwei Mengen, die ein Volumen besitzen. Stimmen die Maße ihrer Schnitte überein, so auch ihre Volumina:
|
[8.5.4] |
-
Die Definition [8.5.2] setzt die Flächenmessung aus 8.4. fort, denn die dort eingeführten Flächenmaßzahlen kommen hier als zweidimensionale Volumina wieder vor: Setzt man nämlich für eine positive Funktion
so besitzt M ein Volumen und ist die Maßzahl der Fläche, die f im Bereich mit der x-Achse einschließt.
Beweis: Für ist , und damit: . Also hat man
Wir üben die Volumenberechnung zunächst im Zweidimensionalen und ermitteln noch einmal einige bekannte Volumina.
Beispiel: |
Quadrat |
Ellipse |
Kreis |
Lochscheibe |
Linie |
Rechteck |
Dreieck |
|
-
Das Quadrat mit Kantenlänge a hat das Volumen
|
[6] |
Beweis: Nach [1] haben die Schnitte in Q ein konstantes Volumen:
ist daher auf integrierbar, so dass Q ein Volumen besitzt, nämlich
-
Die Ellipse mit den Halbachsen a und b hat das Volumen
|
[7] |
Beweis: Nach [2] sind die Schnitte in E die Intervalle
Da die stetige Funktion auf integrierbar ist, hat E ein Volumen, das wir mit einem Integral aus 8.4 berechnen können zu
-
Der Kreis (Disc) mit Radius r hat das Volumen
|
[8] |
Beweis: D ist eine Ellipse mit identischen Halbachsen: . Also ist .
-
Die Lochscheibe mit den Radien hat das Volumen
|
[9] |
Beweis: Nach [3] sind die Schnitte in einer Lochscheibe gegeben durch
Ihr eindimensionales Maß ergibt sich daher (auch im angesprochenen Sonderfall ) zu
ist als Verklebung der Einschränkungen , und darstellbar, nach [8.1.14] also integrierbar. L besitzt daher ein Volumen, und zwar (mit Hilfe eines Integrals aus 8.4)
-
Ist eine Funktion, so hat die Linie f das Volumen
|
[10] |
Beweis: Da sind alle Schnitte einpunktig und haben damit das Volumen 0. Also ist
-
Das Rechteck mit den Kantenlängen a und b hat das Volumen
|
[11] |
Beweis:
?
, die Schnitte haben das konstante Volumen .
R hat daher ein Volumen, und zwar
-
Das Dreieck mit der Grundseite und der Höhe h hat das Volumen
|
[12] |
Beweis:
?
, die Schnitte sind (variable) Intervalle und die Funktion ist integrierbar. Also besitzt D das Volumen
|
In den nächsten Beispielen berechnen wir die klassischen dreidimensionalen Volumina. Wir greifen dabei auf die bereits gewonnenen Ergebnisse [6] bis [9] zurück.
Beispiel: |
Würfel |
Ellipsoid |
Kugel |
Kegel |
Pyramide |
Torus |
Quader |
Zylinder |
|
-
Der Würfel mit Kantenlänge a besitzt das Volumen
Beweis: und die Schnitte (siehe [4]) haben nach [6] das konstante Volumen . W hat damit ein Volumen, und zwar
-
Das Ellipsoid mit den Halbachsen a, b und c besitzt das Volumen
Beweis: Zunächst hat man . Für hat die Ungleichung
nur die Lösung . Für läßt sie sich äquivalent weiterschreiben zu
ist also entweder ein Punkt oder eine Ellipse (siehe [7]) mit den Halbachsen und . hat also das Volumen
Da integrierbar ist, hat nun E ein Volumen, und zwar
-
Die Kugel (Sphäre) mit Radius r besitzt das Volumen
Beweis: S ist ein Ellipsoid mit drei identischen Halbachsen: . Das Volumen der Sphäre ergibt sich daher direkt aus der Volumenformel für das Ellipsoid.
Ohne dieses Ergebnis argumentiert man folgendermaßen: Nach [5] ist
.
ist also ein Kreis mit Radius (bzw. ein Punkt falls ), mit [8] hat man daher . ist stetig, also integerierbar über , S hat daher das Volumen
-
Der Kegel (Conus) mit Höhe h und Radius r besitzt das Volumen
Beweis: Offensichtlich ist und für hat man
.
ist also auch hier wieder ein Kreis (bzw. ein Punkt für ). Mit [8] ergibt sich daher die auf integrierbare Funktion und damit schließlich das Volumen
-
Die Pyramide mit Höhe h und rechteckiger Grundfläche besitzt das Volumen
Beweis: und für ist
also für ein Punkt, sonst ein Rechteck mit den Kantenlängen und . Mit der integrierbaren Funktion hat man nun:
-
Mit den Abkürzungen und ist die Menge
ein Torus mit den Radien r und R.

i  |
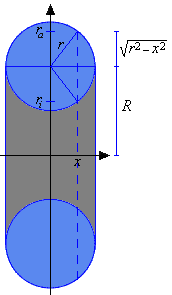 Die nebenstehende Skizze zeigt einen senkrecht zur z-Achse halbierten Torus mit den Radien r und R. Sie erläutert die Berechnung des inneren () und des äußeren () Radius eines Schnittes .
|
Er hat das Volumen
Beweis: und für ein ist der Schnitt
eine Lochscheibe. Nach [9] besitzt das Volumen
ist integrierbar, T besitzt also ein Volumen, nämlich (das auftretende Integral haben wir bereits in 8.4 ermittelt)
-
Der Quader mit den Kantenlängen a, b und c hat das Volumen
Beweis:
?
und für ist , also ein Rechteck mit den Kantenlängen b und c. Da die konstante Funktion über integrierbar ist, besitzt Q das Volumen
-
Der Zylinder
mit Höhe h und Radius r hat das Volumen
Beweis:
?
und für ist ein Kreis mit festem Radius r. ist also wieder konstant und somit integrierbar. Z besitzt daher das Volumen
|
Einige der gerade betrachteten Beispiele (u.a. Kugel und Kegel) respräsentieren eine allgemeine Klasse von Teilmengen des , die ein Volumen besitzen, die sog. Rotationskörper. Sie haben eine drechselförmige Gestalt und entstehen durch Rotation eines Graphen um die x-Achse.
|
Bezeichnung und Bemerkung: Ist eine stetige Funktion, so nennen wir die Menge
|
[8.5.5] |
den durch die Hüllfunktion f (im Bereich ) erzeugten Rotationskörper. R besitzt das Volumen
Beweis: und für ist ein Kreis mit Radius . Man hat also , und damit die Behauptung.
|
Als Beispiel berechnen wir das Volumen des durch die Hüllfunktion in erzeugten Rotationskörpers R (Seilrolle):
|
Aufgabe: Das Ellipsoid

i  |
|
Das Ellipsoid in dieser Aufgabe hat zwei identische Halbachsen, nämlich b in y- und z-Richtung, denn es entsteht durch Rotation der oberen Halbellipse .
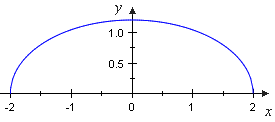
Halbellipse mit a = 2 und b = 1,2
Der für die Schnittkreise benötigte Radius ergibt sich damit aus folgender Rechnung:
|
hat das Volumen .
Beweis:
?
Gemäß Erläuterung ist E der von in erzeugte Rotationskörper. Sein Volumen berechnet sich daher zu
|
Zur Berechnung n-dimensionaler Volumina ist der Einsatz des Induktionsprinzips unerläßlich. Wir beginnen unsere Untersuchungen mit der Berechnung des n-dimensionalen Würfel- bzw. Kugelvolumens.
|
Bemerkung:
-
Der n-dimensionale Würfel hat das Volumen
|
[8.5.6] |
-
Die n-dimensionale Kugel hat das Volumen
|
[8.5.7] |
1. ► Beweis per Induktion:
-
: ist ein abgeschlossenes Intervall mit .
-
: Sei jetzt ein -dimensionaler Würfel. Für ist der Schnitt ein n-dimensionaler Würfel, besitzt also nach Induktionsvoraussetzung ein Volumen. Und da als konstante Funktion auch integrierbar ist, besitzt ebenfalls ein Volumen, und zwar
2. ► Beweis per Induktion:
-
: ist ein geschlossenes Intervall mit
Man beachte, dass hier ist.
-
: Sei jetzt eine ()-dimensionale Kugel. Für ist eine n-dimensionale Kugel, hat also nach Induktionsvoraussetzung ein Volumen. Dabei ist
eine stetige, also auch integrierbare Funktion. besitzt daher ein Volumen.
Mit Hilfe der Substitution (siehe [8.3.5]) berechnen wir zunächst das Integral
und errechnen damit das Volumen der ()-dimensionalen Kugel zu
|
Weitere Untersuchungen führen wir an allgemeinen Zylindern, bzw. allgemeinen Kegeln durch. Für eine nicht-leere Teilmenge
des nennen wir die Menge
-
|
[8.5.8] |
einen (allgemeinen) Zylinder mit Grundfläche G und Höhe h.
-
|
[8.5.9] |
einen (allgemeinen) Kegel (Conus) mit Grundfläche G und Höhe h.
Beachte:
-
Abgesehen vom Fall sind Grundflächen natürlich keine Flächen im gewöhnlichen Sinn.
-
Eine (allgemeine) Pyramide ist ein Kegel, dessen Grundfläche ein Polytop ist.
|
Aufgabe: Besitzt G ein Volumen, so hat der Zylinder das Volumen
|
[8.5.10] |
So hat z.B. der Zylinder , dessen Grundfläche eine Kugel vom Radius 3 ist, ein Volumen von .
Beweis:
?
Ein Induktionsbeweis ist hier nicht erforderlich, denn für alle ist , somit konstant und daher
|
[8.5.10] bestätigt offenbar die alte Formel "Grundfläche mal Höhe" für das Volumen eines Zylinders. Um ein analoges Ergebnis für den Kegel zu erhalten, benötigen wir einige technische Vorbereitungen: Für zwei Vektoren und mit setzen wir für eine beliebige Teilmenge
Dabei schreiben wir abkürzend und , falls bzw. . ist die mit den Streckungsvektor c gestreckte, die um den Verschiebungsvektor d verschobene Menge M.
Die folgende Bemerkung führt nicht nur zu unserem Ziel, sondern auch zu weiteren, wichtigen Ergebnissen.
|
Bemerkung: Eine Teilmenge besitzt genau dann ein Volumen wenn ein Volumen besitzt. In diesem Fall gilt
|
[8.5.11] |
Beweis: Es reicht, nur die Richtung "" nachzuweisen, denn mit der Gleichheit
folgt damit auch die Umkehrung. Wir führen den Beweis nun per Induktion.
-
: Falls , ist auch und beide Mengen haben das Volumen 0. Sei also . Dann ist
wieder eine disjunkte Vereinigung von Intervallen, besitzt also ein Volumen, und
-
: Sei jetzt , also . Falls nun , so ist auch und beide Mengen haben das Volumen 0. Sei daher . Zunächst hat man
[+]
für alle , denn:
Besitzt M nun ein Volumen, so hat jeder Schnitt ein Volumen und ist über integrierbar. Nach Induktionsvoraussetzung hat dann
für jedes das Volumen . Nach [8.3.5] (Substitutionsregel) ist integrierbar, besitzt also ein Volumen, nämlich
|
Wir notieren nun einige Folgerungen aus [8.5.11]:
-
Volumina sind verschiebungstreu, denn mit ist
|
[8.5.12] |
-
Volumina sind streckungskompatibel, denn mit ist
|
[8.5.13] |
-
Volumina sind scherungstreu: Besitzt ein Volumen, so hat für jeden Scherungsvektor die Menge
ein Volumen derselben Größe:
|
[8.5.14] |
Beweis: Für ist offensichtlich . Nach [8.5.12] hat daher das Volumen und mit [8.5.4] (Prinzip des Cavalieri) folgt dann die Behauptung.
Mit der nun vorliegenden Streckungskompatibilität kehren wir zu unserem Vorhaben zurück und berechnen das Volumen eines allgemeinen Kegels.
|
Bemerkung: Der Kegel
hat ein Volumen, falls seine Grundfläche ein Volumen besitzt. In diesem Fall gilt:
|
[8.5.15] |
Beweis: Für ist . Mit G besitzt daher nach [8.5.13] auch ein Volumen, nämlich . Als Vielfaches von ist integrierbar, also besitzt C das Volumen
|
Beachte:
-
Die Volumenformel [8.5.15] erfasst natürlich auch die bereits ermittelten Volumen von Dreiecken, dreidimensionalen Kreiskegeln und Pyramiden.
-
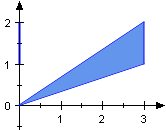
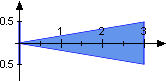
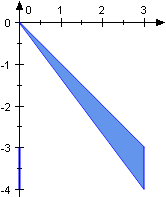
Die Höhe eines Kegels kann, aber muss nicht senkrecht auf der Grundfläche stehen. Für das Volumen ist dies ohne Bedeutung. So haben etwa alle skizzierten Dreiecke dasselbe Volumen 1,5.
|