8.6. Weglängen
Wir schließen den geometrischen Aspekt der Integralrechnung ab mit einem Abschnitt über Wege und deren Längen.
|
Definition: Ist und ein geschlossenes Intervall in , so nennen wir jede Funktion der Form
|
[8.6.1] |
einen Weg (in M). ist der Anfangspunkt und der Endpunkt des Wegs. w heißt geschlossen, falls . Den Bildbereich nennen wir die zu w gehörige Kurve.
Sind alle Koordinatenfunktionen
-
stetig, so ist w ein stetiger Weg (auch: -Weg).
-
differenzierbar, so sprechen wir von einem differenzierbaren Weg (-Weg) und nennen dann die Funktion
|
[8.6.2] |
die Ableitung von w. w heißt regulär falls für alle .
Analog führt man mehrfach differenzierbare Wege und höhere Ableitungen ein.
-
stetig differenzierbar, so nennen wir w einen glatten Weg (-Weg).
-
integrierbar, so ist w ein integrierbarer Weg und für lesen wir den Vektor
|
[8.6.3] |
als das Integral über w von r bis s.
|
Beachte:
Ist eine "gewöhnliche" reellwertige Funktion, so ist ihr Graph die zum Weg
gehörige Kurve. Da X beliebig oft differenzierbar (also auch stetig und integrierbar) ist, hat w genau dieselben Qualtitäten wie f.
Oft stellt man sich unter einem Weg w die Bewegung eines Punktes auf seiner Bahnkurve vor. Das Intervall ist dann der Zeitabschnitt in dem die Bewegung beobachtet wird. Die Schreibweise
(statt ) unterstützt diese Sichtweise. Ist w differenzierbar, so sehen wir in der Ableitung die Geschwindigkeit des Punkts zum Zeitpunkt t.
Zwischen einem Weg und seiner zugehörigen Kurve ist deutlich zu unterscheiden, denn verschiedene Wege können durchaus dieselbe Kurve besitzen. Man betrachte etwa die Wege
Beide Wege haben als Kurve die Verbindungsstrecke von und . Allerdings unterscheiden sie sich in ihrer Laufrichtung: w durchläuft diese Strecke von links nach rechts, v hingegen von rechts nach links.
Auch beim mehrfachen Durchlaufen einer Kurve ändern sich die Wege, aber nicht die Kurve. Ersetzt man etwa im folgenden Beispiel das Intervall durch , so wird die Ellipse k-mal durchlaufen. Ihre Gestalt ändert sich dabei natürlich nicht.
Schließlich beachte man, dass auch beim Ausschneiden konstanter Abschnitte (also für alle ) die Kurve unverändert bleibt, der Weg selbst jedoch nicht.
|
Beispiel:
-
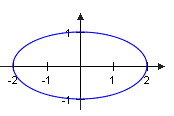 Für ist die Ellipse Für ist die Ellipse
ein geschlossener -Weg in . Die Skizze zeigt die zugehörige Kurve für und .
-
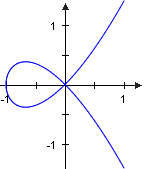 Der -Weg Der -Weg
ist nicht geschlossen. Da und durchläuft die Kurve den Punkt zweimal.
-
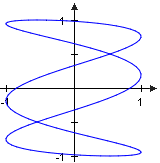 Lissajous-Kurven gehören zu -Wegen der Form Lissajous-Kurven gehören zu -Wegen der Form
Die Skizze zeigt die Lissajous-Kurve zu und . Nicht alle Lissajou-Kurven sind geschlossen.
-
Die
Spirale
i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Spirale
Display by JavaView
|
und die geschlossene
Kurve von Viviani
i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Kurve von Viviani
Display by JavaView
|
sind Beispiele für -Kurven im .
-
Im Famous Curves Index findet man eine Vielzahl weiterer Kurven.
|
Für differenzierbare Wege gelten elementare Ableitungsregeln sowie eine Version des Mittelwertsatzes.
|
Bemerkung:
-
Sind zwei differenzierbare Wege, so ist jede Linearkombination ebenfalls ein differenzierbarer Weg mit
|
[8.6.4] |
-
Ist ein differenzierbarer Weg, so gibt es zu je zwei verschiedenen Punkten Zahlen
zwischen
i   |
|
also , falls
und , falls .
|
r und s, so dass
|
[8.6.5] |
-
Ist ein differenzierbarer Weg, so ist integrierbar und
|
[8.6.6] |
für alle .
Beweis:
1. ► Alle Koordinatenfunktionen sind nach Summen- und Faktorregel differenzierbar mit
2. ► Wir betrachten wieder eine beliebige Koordinatenfunktion und finden über den Mittelwertsatz [7.9.5] ein zwischen r und s, so dass
3. ► Jede Koordinatenfunktion ist trivialerweise eine Stammfunktion zu .
|
Integrale über integrierbare Wege erfüllen dieselben Rechenregeln und haben die gleichen Eigenschaften wie gewöhnliche Integrale auch.
|
Bemerkung: Sind zwei integrierbare Wege, so gilt für
:
-
|
[8.6.7] |
-
|
[8.6.8] |
-
Sind r und s verschieden, so gibt es Zahlen zwischen r und s so dass
|
[8.6.9] |
Beweis: In allen Fällen ist die Gleichheit koordinatenweise zu begründen. Dies gelingt in
1. ► mit [8.2.2] - [8.2.4].
2. ► mit [8.2.5]/[8.2.7].
3. ► mit [8.2.8].
|
Für stetige Wege läßt sich auch die Abschätzung [8.2.11] übertragen. Die Formulierung wie auch der Beweis benutzen dabei das
Skalarprodukt
i   |
|
Mit dem Skalarprodukt
ist insbesondere die Länge eines Vektors gegeben. Im Beweis benutzen wir die leicht einzusehende Identität
,
sowie die Cauchy-Schwarzsche Ungleichung
Ihren Nachweis, sowie weitere Eigenschaften des Skalarprodukts, wie etwa die Dreiecksungleichung
findet man im Abschnitt 9.13.
|
des .
|
Bemerkung: Für jeden stetigen Weg ist
|
[8.6.10] |
Beweis: Man beachte zunächst, dass die stetigen Wege w und auch integrierbar sind. Mit der Abkürzung
, also
wird die folgende Rechnung übersichtlicher. Ist , ist nichts zu zeigen, denn die rechte Seite von [8.6.10] ist stets positiv. Sei also . Mit der Cauchy-Schwarzschen Ungleichung und der Monotonie des Integrals [8.2.10] erhalten wir jetzt die folgende Abschätzung
|
Wir wollen nun die Länge eines stetigen Weges w ermitteln. Bei der Flächenmessung haben wie die anstehende Fläche durch elementare Flächen (Vereinigung von Rechteckstreifen) mit bekanntem Maß approximiert. Hier nun werden wir analog w durch elementare Wege, nämlich die Vereinigung von Strecken approximieren.
Zunächst treffen wir einige technische Vorbereitungen: Unter einer Zerlegung Z des Intervalls verstehen wir eine endliche Sequenz in , , so dass
Die Zahl nennen wir die Feinheit von Z.
Ist w ein vorgegebener Weg, so zeichnet eine Zerlegung Z
Punkte in w aus, deren fortlaufende Verbindungstrecken sich zu einem Polygonzug zusammensetzen:
, falls
|
[8.6.11] |
Alle Polygonzüge sind Wege mit Anfangspunkt und Endpunkt . Sie approximieren einen stetigen Weg w im folgenden Sinn:
|
Bemerkung: Ist ein stetiger Weg, so gibt es zu jedem ein , so dass für jede Zerlegung Z mit einer Feinheit kleiner δ gilt
für alle .
|
[8.6.12] |
Beweis: Sei gegeben. Da jede der stetigen Koordinatenfunktion auf dem abgeschlossenen Intervall auch gleichmäßig stetig ist (siehe [6.5.5]), gibt es zu ein , so dass
Mit hat man daher für mit
[1]
Sei jetzt eine beliebige Zerlegung mit einer Feinheit kleiner als δ. Für ein , etwa , ist dann
und .
Über die Darstellung [8.6.11] und die Abschätzung [1] erhalten wir mit der Dreiecksungleichung nun
|
Die Länge eines solchen Polygonzugs ermitteln wir elementar, indem wir die Längen der Verbindungstrecken aufsummieren. Wir setzen also
|
[8.6.13] |
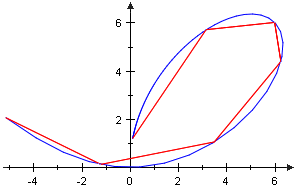 Da die Verbindungsstrecke der kürzeste Weg von nach ist, erwarten wir, dass die Länge von w für jede Zerlegung Z oberhalb von liegt. Wegen [8.6.12] ist daher das
Supremum Da die Verbindungsstrecke der kürzeste Weg von nach ist, erwarten wir, dass die Länge von w für jede Zerlegung Z oberhalb von liegt. Wegen [8.6.12] ist daher das
Supremum
i   |
|
Es sei an das Vollständigkeitsaxiom erinnert:
Jede nicht-leere, beschränkte Teilmenge besitzt in eine kleinste obere Schranke, ihr Supremum (in Zeichen ). Eine obere Schranke s von M ist genau dann gleich , wenn für jedes die Zahl keine obere Schranke von M ist.
|
der Menge ein guter Kandidat für die zu definierende Weglänge.
Die nebenstehende Abbildung zeigt einen Auschnitt eines Kartesischen Blatts von René Descartes, nämlich den Weg . Für ein dreidimensionales Beispiel kommen wir auf die
Spirale
i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Spirale
Display by JavaView
|
aus dem Eingangsbeispiel zurück.
|
Definition: Ein stetiger Weg heißt rektifizierbar oder von endlicher Länge, falls die Menge beschränkt ist. In diesem Fall nennen wir die Zahl
|
[8.6.14] |
die Länge von w.
|
Interessanterweise sind glatte Wege stets rektifizierbar, wobei sich alle Längen durch das Integral über die Länge der Ableitung abschätzen lassen. Allerdings gibt es auch nicht glatte Wege, die eine endliche Länge besitzen, wie etwa das Beispiel

i   |
Ist eine Zerlegung von , so gibt es ein k, so dass . Man weiß daher:
also , und damit
für alle . Mit
können wir nun folgendermaßen abschätzen:
|
zeigt.
|
Bemerkung: Ist ein glatter Weg, so gilt für jede Zerlegung Z von :
|
[8.6.15] |
w ist damit rektifizierbar.
Beweis: Mit der Darstellung [8.6.6], der Abschätzung [8.6.10] und der Zerlegungseigenschaft [8.6.7] erhalten wir für eine beliebige Zerlegung :
.
|
[8.6.15] läßt sich deutlich verschärfen: Das Integral über ist nicht nur irgendeine obere Schranke der Menge , sondern ihre kleinste und damit ihr Supremum.
|
Bemerkung: Für jeden glatten Weg gilt:
|
[8.6.16] |
Beweis: Nach [8.6.15] ist eine obere Schranke von . Es reicht daher, zu jedem eine Zerlegung Z zu finden, so dass
.
Da die Koordinatenfunktionen stetig differenzierbar sind, sind die Funktionen stetig, auf dem geschlossenen Intervall also auch gleichmäßig stetig. Zu gibt es daher ein so dass für alle gilt
[2]
Man wähle jetzt eine Zerlegung , deren Feinheit kleiner als ist. Dann gibt es nach [8.2.8] bzw. [8.6.5] Zahlen
-
so dass [3]
-
so dass
[4]
Da hat man für alle i
.
Mit [2] weiß man daher , so dass wir gemäß [3] und [4] das Integral über folgendermaßen abschätzen können (beachte dabei: für positive x, y):
Damit ist die Abschätzung gesichert. ist also die kleinste obere Schranke von , ihr Supremum also.
|
Beschreibt ein Weg die Bewegung eines Punktes, so läßt sich nach [8.6.16] der dabei zurück gelegte Weg offenbar durch das Integral über den Betrag seiner Geschwindigkeit berechnen.
Obwohl [8.6.16] die (meist schwierige) Ermittlung eines Supremums durch die Berechnung eines Integrals ersetzt, läßt sich eine Weglänge selten leicht bestimmen. Der Integrand nämlich ist immer die Länge eines Vektors, also die Wurzel aus einer Summe positiver Funktionen. Die folgenden Beispiele machen dies deutlich.
|
Beispiel:
-
Der glatte Weg
bildet die Verbindungsstrecke der Punkte und des . Mit der konstanten Ableitung berechnen wir ihre Länge zu
Die Länge stimmt also, wie erwartet, mit dem Abstand der Punkte a und b überein.
-
Wir berechnen für ein beliebiges die Länge der durch
gegebenen Spirale aus dem Eingangsbeispiel:
Mit , also (mit dem Satz von Pythagoras: )
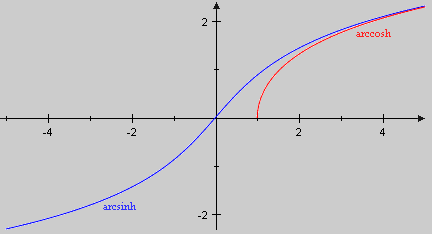
Zur Berechnung des Integrals benötigen wir die hyperbolischen Funktionen
sinh und cosh
i   |
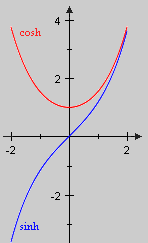 Der hyperbolische Sinus (sinus hyperbolicus) und der hyperbolische Kosinus (cosinus hyperbolicus) werden über die Exponentialfunktion exp (siehe [5.9.18]) definiert. Für setzen wir
[0]
Beide Funktionen sind beliebig oft differenzierbar und mit (siehe [7.5.8]) bestätigt man sofort die Ableitungen
und .
Auch die folgenden Eigenschaften ergeben sich direkt aus der Definition [0]:
-
-
-
-
-
-
sinh ist sowohl injektiv (gemäß [7.9.6], denn für alle x), wie auch surjektiv (eine Folgerung aus dem Zwischenwertsatz [6.6.2], denn sinh ist stetig und ), insgesamt also bijektiv. Die Umkehrfunktion
ist der arcussinus hyberbolicus. Auf dieselbe Weise begründet man auch die Existenz des arcuscosinus hyperbolicus, der Umkehrfunktion von :
|
. Da eine Stammfunktion zu ist

i   |
|
Wir benutzen den Hauptsatz [8.2.13] und berechnen mittels partieller Integration (siehe [8.3.1]) für ein beliebiges x das Integral
Also ist eine Stammfunktion zu .
|
, können wir mit der Substitution (siehe [8.3.5]) folgendermaßen fortfahren:
-
Erstaunlicherweise gelingt es nicht, für die Kurvenlänge einer Ellipse
einen geschlossenen Ausdruck anzugeben. Das Integral
ist ein sog. elliptisches Integral und läßt sich nur für die trivialen Fälle und ausrechnen. Im letzten Fall allerdings, wenn also ist, stellt die Ellipse einen Kreis mit Radius dar, dessen Umfang wir somit zu
berechnen können.
Aufgaben:
-
Für ist und damit
-
Für das Parabelsegment ist . Also ist
und da eine Stammfunktion zu ist, folgt schließlich
|
Die Länge eines glatten Wegs läßt sich besonders leicht ausrechnen, wenn der Ableitungsvektor eine konstante Länge hat. Im Fall ist sogar
für alle . Der Wegabschnitt ist also genauso lang wie der zugehörige Intervallabschnitt. Wir sagen dann, w sei nach der Bogenlänge parametrisiert. Reguläre Wege können stets nach der Bogenlänge parametrisiert werden.
|
Bemerkung: Ist ein regulärer Weg, so gibt es eine differenzierbare Bijektion mit folgenden Eigenschaften:
-
ist nach der Bogenlänge parametrisiert.
-
und w erzeugen diesselbe Kurve.
-
.
|
[8.6.17] |
Beweis: Gemäß Hauptsatz [8.2.13] ist die Funktion , gegeben durch
,
eine Stammfunktion zu . Da w regulär ist, weiß man: für alle . Nach [7.9.6] ist s daher injektiv und
in jedem differenzierbar mit (siehe [7.5.4])
Schließlich garantiert der Zwischenwertsatz [6.6.2], dass , denn und . Nach Kettenregel [7.7.8] ist daher ein regulärer Weg mit
Jetzt zeigen wir:
1. ►
2. ► Da bijektiv ist, hat man:
3. ►
|
|
 |
|
 Für ist die Ellipse
Für ist die Ellipse Der -Weg
Der -Weg
 Da die Verbindungsstrecke der kürzeste Weg von nach ist, erwarten wir, dass die Länge von w für jede Zerlegung Z oberhalb von liegt. Wegen
Da die Verbindungsstrecke der kürzeste Weg von nach ist, erwarten wir, dass die Länge von w für jede Zerlegung Z oberhalb von liegt. Wegen