8.7. Die Logarithmusfunktion
Dieser Abschnitt beschäftigt sich allein mit der Kehrwertfunktion. Sie ist die einzige Potenzfunktion, über deren Stammfunktionen wir bislang keine Kenntnis haben. Allerdings ist die Kehrwertfunktion stetig, auf Intervallen muss sie daher nach [8.1.5] integrierbar sein!
Eine ihrer Stammfunktionen auf zeichnen wir durch einen eigenen Namen aus. Wir verwenden dabei den Hauptsatz [8.2.13]:
|
Definition: Die Funktion , gegeben durch
|
[8.7.1] |
heißt der (natürliche) Logarithmus oder auch die (natürliche) Logarithmusfunktion.
|
Beachte:
-
Der Funktionsname ist die Abkürzung des lateinischen Namens logarithmus naturalis.
-
Wie bei den trigonometrischen Funktionen auch ist es üblich, statt zu schreiben.
-
Die untere Integrationsgrenze 1 in [8.7.1] legt den Wert fest.
-
Als Stammfunktion zu ist ln bereits differenzierbar mit . Damit ist ln sofort beliebig oft differenzierbar, , und insbesondere auch stetig ([7.5.2]).
-
Als stetige Funktion ist auf dem Intervall integrierbar. Mit Hilfe der partiellen Integration [8.3.1] (und einem kleinen Trick) können wir eine ihrer Stammfunktionen über den Hauptsatz errechnen. Für ist nämlich:
Also ist (auch) eine Stammfunktion zu .
-
Mit der Kettenregel [7.7.8] und der Ableitung von (siehe [7.4.3]) berechnen wir
,
so dass wir als eine Stammfunktion zur vollständigen Kehrwertfunktion bestätigen können.
Weitere Eigenschaften der Logarithmusfunktion lassen sich direkt aus der Integraldarstellung gewinnen.
|
Bemerkung:
|
1.
|
[8.7.2] |
|
2. ist streng monoton wachsend
|
[8.7.3] |
|
3. für alle
|
[8.7.4] |
|
4. für alle
|
[8.7.5] |
Beweis:
1. ►
2. ► Für alle ist . Die Behauptung folgt also aus der strengen Variante des Monotoniesatzes [7.10.5].
3. und 4. ergeben sich direkt aus 1. und 2.
|
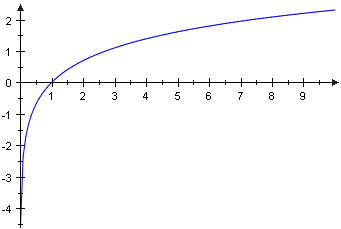 Bereits aus diesen wenigen Angaben läßt sich der charakteristische Graphenverlauf des Logarithmus ableiten. Die unterstellte Unbeschränktheit wird allerdings erst am Ende dieses Abschnitts durch den Nachweis der Umkehrbarkeit erhärtet. Bereits aus diesen wenigen Angaben läßt sich der charakteristische Graphenverlauf des Logarithmus ableiten. Die unterstellte Unbeschränktheit wird allerdings erst am Ende dieses Abschnitts durch den Nachweis der Umkehrbarkeit erhärtet.
Mit Hilfe der Substitutionsregel gelingt es, die typischen Rechenregeln für den Logarithmus, die Logarithmengesetze, zu beweisen.
|
Bemerkung (Rechenregeln für ln): Für alle , gilt:
|
1.
|
[8.7.6] |
|
2.
|
[8.7.7] |
|
3.
|
[8.7.8] |
|
4.
|
[8.7.9] |
|
5. für
|
[8.7.10] |
Beweis:
1. ► Wir setzen die Substitutionsregel [8.3.5] ein:
2. ► ergibt sich mit direkt aus 1.
3. ► Wir arbeiten noch einmal mit der Substitutionsregel:
4. ► führen wir auf 2. und 3. zurück: .
5. ► Mit 1. hat man: , und damit die Behauptung.
|
Für die weitere Untersuchung der Logarithmusfunktion benötigen wir als technisches Hilfsmittel eine Abschätzung, die sog. zentrale Ungleichung für .
|
Bemerkung: Für jedes ist
|
[8.7.11] |
Beweis: Für ist nichts zu zeigen. Sei nun zunächst . Da für alle , folgt hier die Behauptung aus dem Monotonieverhalten des Integrals ([8.2.10]):
Ist , so ist . Also erhält man mit dem gerade gewonnenen Ergebnis:
|
Mit steht uns bisher erst ein Funktionswert des Logarithmus zur Verfügung. Über die zentrale Ungleichung können wir nun zusätzlich den Funktionswert der Eulerschen Zahl (siehe [5.7.7]) ermitteln.
|
Bemerkung:
|
[8.7.12] |
Beweis: Wir betrachten zunächst die Folge . Mit [8.7.11] gelingt die folgende Abschätzung:
Da , erhält man mit dem Schachtelsatz [5.5.8]: . Schließlich garantiert die Stetigkeit von ln die Behauptung:
|
Interessanterweise ist es über die zentralen Ungleichung sogar möglich, Zugang zu allen Funktionswerten von ln zu finden. Dazu benötigen wir zunächst eine Erweiterung der zentralen Ungleichung: Wendet man [8.7.11] auf
an, so erhält man mit [8.7.10] für alle die Abschätzung
.
|
[8.7.13] |
Die beiden einschachtelnden Folgen erweisen sich dabei als konvergent gegen einen gemeinsamen Limes:
|
Bemerkung: Für alle ist
|
|
[8.7.14] |
Beweis: Wir beweisen beide Aussagen gleichzeitig und zeigen dazu der Reihe nach:
-
ist konvergent.
-
.
1. ► Gemäß [8.7.13] ist nach unten beschränkt (durch ). Nach [5.7.1] genügt es daher zu zeigen: ist monoton fallend, d.h.
für alle . Über die
Bernoullische Ungleichung
i   |
für alle
Beweis: [2] ergibt sich direkt aus der gewöhnlichen Bernoullischen Ungleichung [5.2.6], denn da , hat man:
,
und damit:
Zum Nachweis von [1] setzen wir das gerade erzielte Ergebnis ein und erhalten:
Bei der letzten Abschätzung beachte man, dass das Weglassen des Summanden den Nenner von vergrößert, falls der Zähler positiv ist, bzw. verkleinert, wenn der Zähler negativ ist. In jedem Fall aber verkleinert sich dabei der gesamte Bruch.
|
für die n-te Wurzel erhalten wir zunächst:
.
Die Abschätzung [+] ergibt sich nun, wenn man x durch ersetzt.
2. ► Da (siehe [5.7.9]) folgt die Behauptung aus dem dritten Grenzwertsatz [5.6.3]:
Das Ergebnis in 2. zeigt nun: Mit ist auch konvergent, und zwar gegen einen gemeinsamen Limes, der wegen [8.7.13] die Zahl sein muss. Das Argument ist dabei der Schachtelsatz [5.5.8].
|
Eine weitere Anwendung der zentralen Ungleichung belegt nun die Umkehrbarkeit des Logarithmus.
|
Bemerkung: Jedes besitzt genau ein Urbild , d.h.
ist bijektiv.
|
[8.7.15] |
Beweis: Da für alle ist nach [7.9.6] zunächst injektiv, d.h. jedes hat höchstens ein Urbild.
Ein solches y hat aber auch mindestens ein Urbild, denn mit der zentralen Ungleichung [8.7.11] hat man zunächst und damit für ein beliebiges :
Da in unbeschränkt ist, gibt es nun zu y ein , so dass . Damit liegt y zwischen zwei ln-Werten und muss daher aufgrund des Zwischenwertsatzes [6.6.2] ein Funktionswert von ln sein. ln ist also auch surjektiv.
|
[8.7.15] zeigt insbesondere, dass ln in beide Richtungen unbeschränkt wächst, d.h. und . Interessant ist dabei die Art dieses Wachstums:
-
ln strebt für langsamer gegen als jede positive Potenz, d.h. für hinreichend große x.
-
ln strebt für langsamer gegen als jede negative Potenz, d.h. für hinreichend kleine x.
Die folgende Bemerkung präzisiert diese Vorstellungen.
|
Bemerkung: Für jedes *) gilt:
|
1.
|
[8.7.16] |
|
2.
|
[8.7.17] |
___________
*) Potenzen mit beliebigen Exponenten werden in 8.9 eingeführt.
Beweis: Wir wählen ein so dass , also , und setzen wieder die zentrale Ungleichung [8.7.11] ein:
1. ► Für alle ist
.
Da nun , folgt daher die Behauptung.
2. ► Hier hat man für alle :
,
so dass die Behauptung jetzt aus folgt.
|
Funktionen des Typs und konnten wir in [8.1.11-12] leicht mit einer Stammfunktion versorgen. Mit Hilfe der Logarithmusfunktion finden wir auch für den Typ ein passendes Verfahren.
|
Bemerkung (Logarithmische Integration): Ist differenzierbar, so ist integrierbar und
ist eine Stammfunktion zu .
|
[8.7.18] |
Beweis: ist gemäß Kettenregel ([7.7.8]) differenzierbar, und zwar mit folgender Ableitung:
|
So hat man zum Beispiel:
-
-
-
Für ist , so dass wir mit eine Stammfunktion zu ermittelt haben.
|
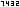 |
|
 Bereits aus diesen wenigen Angaben läßt sich der charakteristische Graphenverlauf des Logarithmus ableiten. Die unterstellte Unbeschränktheit wird allerdings erst am Ende dieses Abschnitts durch den Nachweis der Umkehrbarkeit erhärtet.
Bereits aus diesen wenigen Angaben läßt sich der charakteristische Graphenverlauf des Logarithmus ableiten. Die unterstellte Unbeschränktheit wird allerdings erst am Ende dieses Abschnitts durch den Nachweis der Umkehrbarkeit erhärtet.