7.10. Geometrische Eigenschaften differenzierbarer Funktionen

Im letzten Abschnitt haben wir über den Mittelwertsatz belegen können, dass das Verhalten einer Funktion f durch ihre eigene Ableitung

f^{'}

gesteuert wird.

Wir studieren nun zwei geometrisch orientierte Aspekte genauer: Das Monotonie- und das Krümmungsverhalten einer Funktion. Wir werden dabei sehen, dass sich die Monotonie durch die erste und die Krümmung durch die zweite Ableitung beschreiben läßt.

Definition: Eine Funktion $f : A \to ℝ$ heißt auf einer Teilmenge $B \subset A$

monoton steigend (oder auch monoton wachsend), falls für alle $x, y \in B$ gilt:

x < y \Rightarrow f (x) \leq f (y)

[7.10.1]

monoton fallend, falls für alle $x, y \in B$ gilt:

x < y \Rightarrow f (x) \geq f (y)

[7.10.2]

Wir nennen f auf B streng monoton steigend, falls die Folgerung in [7.10.1] zu $f (x) < f (y)$ verschärft werden kann. Analog richten wir die Eigenschaft streng monoton fallend ein.

Den Zusatz "auf B" verwenden wir nur, falls $A \neq B$ ist.

Beachte:

Offensichtlich sind die konstanten Funktionen gleichzeitig monoton steigend und fallend. Sie sind aber auch die einzigen dieser Art, denn erfüllt $f : A \to ℝ$ beide Monotoniebedingungen, so hat man für zwei beliebige Punkte $x, y \in A$ :

$f (x) \leq f (y) \land f (x) \geq f (y) \Rightarrow f (x) = f (y)$

Je zwei Funktionswerte sind somit identisch. Für ein festes $a \in A$ etwa hat man: $f (x) = f (a)$ für alle $x \in A$ .
Gelegentlich ist es von Vorteil, die Monotoniebedingungen leicht umzuformulieren. So ist
- [7.10.1] äquivalent zu: $y - x > 0 \Rightarrow f (y) - f (x) \geq 0$ [1]
- [7.10.2] äquivalent zu: $y - x > 0 \Rightarrow f (y) - f (x) \leq 0$ [2]

Über die Varianten [1] und [2] stellt sich eine interessante Nähe zu den Differenzenquotientenfunktionen ein:

Bemerkung: Eine Funktion $f : A \to ℝ$ ist auf $B \subset A$ genau dann

monoton steigend, wenn für je zwei verschiedene $x, y \in B$ gilt:

\frac{f (y) - f (x)}{y - x} \geq 0

[7.10.3]

monoton fallend, wenn für je zwei verschiedene $x, y \in B$ gilt:

\frac{f (y) - f (x)}{y - x} \leq 0

[7.10.4]

Beweis: Wir zeigen nur die erste Behauptung. Der Beweis der zweiten verläuft nahezu identisch.

" $\Rightarrow$ ": Sei f monoton steigend. Aus Variante [1] entnehmen wir für $x \neq y$ : Die Differenzen $y - x$ und $f (y) - f (x)$ haben dasselbe Vorzeichen, ihr Quotient $\frac{f (y) - f (x)}{y - x}$ ist daher stets positiv.

" $\Leftarrow$ ": Ist nun $y - x > 0$ , so muss $f (y) - f (x) \geq 0$ gelten, denn andernfalls wäre $\frac{f (y) - f (x)}{y - x} < 0$ im Gegensatz zur Voraussetzung.

Für differenzierbare Funktionen auf Intervallen gewinnen wir aus diesem Kriterium den Monotoniesatz, eine Charakterisierung der Monotonie über das Ableitungsverhalten von f. Damit steht uns die angestrebte geometrische Deutung der ersten Ableitung $f^{'}$ zur Verfügung.

Bemerkung (Monotoniesatz): Ist f differenzierbar auf einem Intervall I, also $f \in D^{1} (I)$ , so gilt

f ist monoton steigend auf I $\Leftrightarrow f^{'} (x) \geq 0 für alle x \in I$

[7.10.5]

f ist monoton fallend auf I $\Leftrightarrow f^{'} (x) \leq 0 für alle x \in I$

[7.10.6]

Beweis: Wir zeigen wieder nur 1.

" $\Rightarrow$ ": Ist f monoton steigend, so wissen wir gemäß [7.10.3]:

m_{x} (y) = \frac{f (y) - f (x)}{y - x} \geq 0

für alle

y \in I \ {x}

Nach [6.9.4] ist daher $f^{'} (x) = \lim_{y \to x} m_{x} (y) \geq 0$ .

" $\Leftarrow$ ": Sei nun $x, y \in I$ , so dass $x < y$ . Nach Mittelwertsatz [7.9.5] gibt es dann ein $\tilde{x} \in] x, y [$ mit

f (y) = f (x) + \underset{> 0}{\underset{︸}{(y - x)}} \cdot \underset{\geq 0}{\underset{︸}{f^{'} (\tilde{x})}} \geq f (x)

Beachte:

Die Beweisrichtung " $\Leftarrow$ " zeigt einen typischen Einsatz des Mittelwertsatzes. An den Details erkennt man, dass

das geforderte Ableitungsverhalten tatsächlich nur an den inneren Punkten von I vorliegen muss.
sich die Richtung " $\Leftarrow$ " auch auf die strenge Monotonie übertragen läßt. Man hat also:
1. $f^{'} (x) > 0$ für alle x aus dem Inneren von I $\Rightarrow$ f ist streng monoton steigend auf I.
2. $f^{'} (x) < 0$ für alle x aus dem Inneren von I $\Rightarrow$ f ist streng monoton fallend auf I.
Da $(X^{3})^{'} (0) = 0$ , zeigt das Beispiel der streng wachsenden Funktion $X^{3}$ , dass eine volle Äquivalenz nicht erreicht werden kann.

Über die Monotonie stehen uns nun weitere Möglichkeiten zur Verfügung, eine lokale Extremstelle zu bestätigen, hinreichende Kriterien also (Vergleiche dazu das notwendige Kriterium [7.9.2] und das hinreichende Kriterium [7.9.17] für $C^{n + 1}$ -Funktionen). Wir beginnen mit der Beobachtung, dass am Übergang zweier verschiedener Monotoniebereiche ein lokales Extremum vorliegen muss.

Bemerkung: $f : A \to ℝ$ besitzt in $a \in A$ ein lokales Extremum, falls es ein $ε > 0$ gibt, so dass f auf den relativen Halbumgebungen

A \cap] a - ε, a]

und

A \cap [a, a + ε [

[7.10.7]

ein unterschiedliches Monotonieverhalten hat. Die Umkehrung ist i.A. falsch.

Beweis: Sei f etwa monoton steigend auf $A \cap] a - ε, a]$ und monoton fallend auf $A \cap [a, a + ε [$ . Dann gilt für alle $x \in$ $A_{a, ε}$
i

$A_{a, ε} = A \cap] a - ε, a + ε [$

:

\begin{array}{l} f (x) \leq f (a),  falls x \leq a \\ f (a) \geq f (x),  falls x \geq a \end{array}

f besitzt also in a ein lokales Maximum.

Mit einem Beispiel zeigen wir, dass dieses Kriterium nicht umkehrbar ist: Die Indikatorfunktion $χ_{ℚ}$
i

$χ_{ℚ} (x) = {\begin{array}{l} 1, falls x \in ℚ \\ 0, falls x \notin ℚ \end{array}$
besitzt in 0 ein globales Minimum, ist aber in keinem Intervall monoton.

Für differenzierbare Funktionen auf Intervallen ergibt sich daraus ein weiteres hinreichendes Kriterium (" $f^{'}$ besitzt in a eine Nullstelle mit Vorzeichenwechsel ").

Bemerkung: Eine Funktion $f \in D^{1} (I)$ besitzt in $a \in I$ ein lokales Extremum, falls es ein $ε > 0$ gibt, so dass $f^{'}$ auf den Halbumgebungen

I \cap] a - ε, a]

und

I \cap [a, a + ε [

[7.10.8]

ein unterschiedliches Vorzeichen hat. Die Umkehrung ist i.A. falsch.

Beweis: Hat $f^{'}$ auf den Intervallen $I \cap] a - ε, a]$ und $I \cap [a, a + ε [$ ein unterschiedliches Vorzeichen, also etwa $f^{'} (x) \geq 0$ für alle $x \in I \cap] a - ε, a]$ und $f^{'} (x) \leq 0$ für alle $x \in I \cap] a, a + ε]$ , so zeigt f dort nach [7.10.5./6.] ein unterschiedliches Monotonieverhalten, besitzt daher gemäß [7.10.7] ein lokales Extremum in a.

Die Funktion $f : ℝ \to ℝ$ gegeben durch

f (x) ≔ {\begin{array}{l} 0,  falls x = 0 \\ (x \cdot \sin x^{- 1})^{2},  falls x \neq 0 \end{array}

zeigt, dass [7.10.8] nicht umkehrbar ist. f ist nämlich differenzierbar mit

f^{'} (x) = {\begin{array}{l} \lim_{y \to 0} \frac{(y \cdot \sin y^{- 1})^{2}}{y} = \lim_{y \to 0} y \cdot \sin^{2} y^{- 1} = 0,  falls x = 0 (beachte: \sin^{2} ist beschränkt!) \\ 2 (x \cdot \sin x^{- 1}) (\sin x^{- 1} - x^{- 1} \cdot \cos x^{- 1}) = 2 x \cdot \sin^{2} x^{- 1} - 2 \cdot \sin x^{- 1} \cdot \cos x^{- 1},  falls x \neq 0 \end{array}

und hat in 0 ein globales Minimum. In jeder Halbumgebung von 0 aber wechselt $f^{'}$ beliebig oft das Vorzeichen. Wir zeigen dies beispielhaft für eine rechte Halbumgebung und berechnen dazu für ein beliebiges $n \in ℕ^{*}$ die Werte $f^{'} ((n π + \frac{π}{4})^{- 1})$ und $f^{'} ((n π + 3 \frac{π}{4})^{- 1})$ .

Zunächst erhalten wir über die Additionstheoreme [4.3.*] für sin und cos:

\begin{array}{l} \sin (n π + \frac{π}{4}) = \underset{= 0}{\underset{︸}{\sin (n π)}} \cdot \cos \frac{π}{4} + \cos (n π) \cdot \underset{= \frac{\sqrt{2}}{2}}{\underset{︸}{\sin \frac{π}{4}}} = \cos (n π) \cdot \frac{1}{2} \sqrt{2} \\ \cos (n π + \frac{π}{4}) = \cos (n π) \cdot \underset{= \frac{\sqrt{2}}{2}}{\underset{︸}{\cos \frac{π}{4}}} - \underset{= 0}{\underset{︸}{\sin (n π)}} \cdot \sin \frac{π}{4} = \cos (n π) \cdot \frac{1}{2} \sqrt{2} \\ \sin (n π + 3 \frac{π}{4}) = \underset{= 0}{\underset{︸}{\sin (n π)}} \cdot \cos 3 \frac{π}{4} + \cos (n π) \cdot \underset{= \frac{\sqrt{2}}{2}}{\underset{︸}{\sin 3 \frac{π}{4}}} = \cos (n π) \cdot \frac{1}{2} \sqrt{2} \\ \cos (n π + 3 \frac{π}{4}) = \cos (n π) \cdot \underset{= - \frac{\sqrt{2}}{2}}{\underset{︸}{\cos 3 \frac{π}{4}}} - \underset{= 0}{\underset{︸}{\sin (n π)}} \cdot \sin 3 \frac{π}{4} = - \cos (n π) \cdot \frac{1}{2} \sqrt{2} \end{array}

und da $(\cos (n π) \cdot \frac{1}{2} \sqrt{2})^{2} = \frac{1}{2}$ , ergibt sich daraus:

\begin{array}{l} f^{'} ((n π + \frac{π}{4})^{- 1}) = 2 (n π + \frac{π}{4})^{- 1} \cdot \frac{1}{2} - 2 \cdot \frac{1}{2} = (n π + \frac{π}{4})^{- 1} - 1 < 0 \\ f^{'} ((n π + 3 \frac{π}{4})^{- 1}) = 2 (n π + 3 \frac{π}{4})^{- 1} \cdot \frac{1}{2} + 2 \cdot \frac{1}{2} = (n π + \frac{π}{4})^{- 1} + 1 > 0 \end{array}

Für eine weitere geometrische Untersuchung betrachten wir die beiden dargestellten Graphenausschnitte.

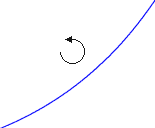
Beide haben denselben Start- und denselben Endpunkt. Sie unterscheiden sich zwar nicht im Monotonie-, wohl aber im Krümmungsverhalten: Der erste ist links-, der zweite dagegen rechtsgekrümmt.

Diese unterschiedliche Orientierung verrät sich durch den Sekantentest: Legt man eine beliebige Sekante an den Graphen, so liegt im ersten Fall der Graph unterhalb, im zweiten oberhalb der Sekante. Diese Beobachtung motiviert die folgende Definition.

Definition: Eine Funktion $f : A \to ℝ$ heißt auf einer Teilmenge $B \subset A$

konvex (oder auch linksgekrümmt), falls für alle $a, b \in B$ mit $a < b$ gilt:

f (x) \leq f (a) + \frac{f (b) - f (a)}{b - a} (x - a) für alle x \in] a, b [\cap B

[7.10.9]

konkav (oder auch rechtsgekrümmt), falls für alle $a, b \in B$ mit $a < b$ gilt:

f (x) \geq f (a) + \frac{f (b) - f (a)}{b - a} (x - a) für alle x \in] a, b [\cap B

[7.10.10]

Gilt in [7.10.9] sogar $<$ statt $\leq$ , so nennen wir f auf B streng konvex. Analog definieren wir die Eigenschaft streng konkav.

Den Zusatz "auf B" verwenden wir nur, falls $A \neq B$ ist.

Beachte:

Multipliziert man [7.10.9] mit −1, so erkennt man den Zusammenhang

f ist konvex $\Leftrightarrow - f$ ist konkav.
Eine lineare Funktion f ist gleichzeitig links- und rechtsgekrümmt, denn für je zwei verschiedene Punkte $a, b \in ℝ$ ist $f = f (a) + \frac{f (b) - f (a)}{b - a} (X - a)$ . Ist umgekehrt eine Funktion $f : ℝ \to ℝ$ sowohl konvex wie auch konkav, so gilt zunächst für ein beliebiges $n \in ℕ^{> 1}$ und alle $x \in] - n, n [$ :

$\begin{array}{l} f (x) & = f (- n) + \frac{f (n) - f (- n)}{2 n} (x + n) \\ = f (- n) + \frac{f (n) - f (- n)}{2} + \frac{f (n) - f (- n)}{2 n} x \end{array}$ [3]

und daraus speziell:

$\begin{array}{l} f (0) = f (- n) + \frac{f (n) - f (- n)}{2} \\ f (1) = f (- n) + \frac{f (n) - f (- n)}{2} + \frac{f (n) - f (- n)}{2 n} = f (0) + \frac{f (n) - f (- n)}{2 n} . \end{array}$

Mit $\frac{f (n) - f (- n)}{2 n} = f (1) - f (0)$ läßt sich [3] nun unabhängig von n formulieren:

$f (x) = f (0) + (f (1) - f (0)) x$ .

Diese Gleichung gilt aber für alle x, denn jedes x liegt in einem Intervall der Form $] - n, n [$ . f ist damit linear.

Wir betrachten nun einige Eigenschaften konvexer Funktionen. Alle gelten sinngemäß auch für konkave Funktionen und, bis auf geringe Ausnahmen, auch für die jeweiligen strengen Fälle.

Zunächst erhält man durch bloßes Umstellen (beachte: $x - a > 0$ !) von [7.10.9] in der Forderung

\frac{f (x) - f (a)}{x - a} \leq \frac{f (b) - f (a)}{b - a} für alle x \in] a, b [\cap B

[4]

eine äquivalente Bedingung für die Konvexität von f. Beachtet man ferner, dass die Geraden

f (a) + \frac{f (b) - f (a)}{b - a} (X - a)

und

f (b) + \frac{f (b) - f (a)}{b - a} (X - b)

identisch sind, [7.10.9] also auch durch $f (x) \leq f (b) + \frac{f (b) - f (a)}{b - a} (x - b)$ ersetzt werden kann, so ergibt sich als weitere äquivalente Bedingung (beachte: $x - b < 0$ !):

\frac{f (x) - f (b)}{x - b} \geq \frac{f (b) - f (a)}{b - a} für alle x \in] a, b [\cap B

[5]

Aus der Kombination von [4] und [5] ergibt sich eine dritte, technisch interessantere Beschreibung der Konvexität.

Bemerkung: $f : A \to ℝ$ ist genau dann konvex auf $B \subset A$ , wenn für beliebige $a, b \in B$ mit $a < b$ gilt:

\frac{f (x) - f (a)}{x - a} \leq \frac{f (b) - f (x)}{b - x} für alle x \in] a, b [\cap B

[7.10.11]

Beweis: Für alle $x \in] a, b [\cap B$ sind die folgenden Ungleichungen äquivalent:

\begin{matrix} \frac{f (x) - f (a)}{x - a} & \leq & \frac{f (b) - f (x)}{b - x} \\ \Leftrightarrow & f (x) (\frac{1}{x - a} + \frac{1}{b - x}) & \leq & \frac{f (a)}{x - a} + \frac{f (b)}{b - x} \\ \Leftrightarrow & f (x) (\underset{= b - a}{\underset{︸}{b - x + x - a}}) & \leq & f (a) (\underset{= b - a + a - x}{\underset{︸}{b - x}}) + f (b) (x - a) \\ = & f (a) (b - a) + (f (b) - f (a)) (x - a) \\ \Leftrightarrow & f (x) & \leq & f (a) + \frac{f (b) - f (a)}{b - a} (x - a) \end{matrix}

Diese Vorbereitungen erlauben es nun, für differenzierbare Funktionen auf Intervallen deutlich bequemere Kriterien für die Konvexität zu notieren.

Bemerkung:

Für $f \in D^{1} (I)$ gilt:

f ist konvex

\Leftrightarrow f^{'}

ist monoton steigend

[7.10.12]

Für $f \in D^{2} (I)$ gilt:

f ist konvex

\Leftrightarrow {f^{'}}^{'} (x) \geq 0 für alle x \in I

[7.10.13]

Beweis:

1. ► Zum Nachweis der Richtung " $\Rightarrow$ " geben wir uns zwei Punkte a und b aus I vor, so dass $a < b$ . Gemäß [4] und [5] gilt dann für alle $x \in] a, b [$ :

m_{a} (x) = \frac{f (x) - f (a)}{x - a} \leq \frac{f (b) - f (a)}{b - a} \leq \frac{f (x) - f (b)}{x - b} = m_{b} (x)

Da $f^{'} (a) = \lim_{x \to a} m_{a} (x) = \lim_{x \to a} m_{a} |] a, b [(x)$ und $f^{'} (b) = \lim_{x \to b} m_{b} (x) = \lim_{x \to b} m_{b} |] a, b [(x)$ (siehe dazu [6.9.1]), folgt somit:

f^{'} (a) \leq \frac{f (b) - f (a)}{b - a} \leq f^{'} (b)

$f^{'}$ ist also monoton steigend.

" $\Leftarrow$ ": Sei jetzt $x \in] a, b [$ , $a, b \in I$ . Gemäß Mittelwertsatz [7.9.4] finden wir zwei Punkte ${\tilde{x}}_{1}, {\tilde{x}}_{2}$ mit $a < {\tilde{x}}_{1} < x < {\tilde{x}}_{2} < b$ , so dass unter Berücksichtigung der Monotonie von $f^{'}$ die folgende Ungleichung gilt:

\frac{f (x) - f (a)}{x - a} = f^{'} ({\tilde{x}}_{1}) \leq f^{'} ({\tilde{x}}_{2}) = \frac{f (b) - f (x)}{b - x}

Dies stellt nach [7.10.11] die Konvexität von f sicher.

2. ► folgt jetzt sofort aus [7.10.5].

Beachte:

Wie beim Einsatz des Mittelwertsatzes üblich, gilt für die Richtung " $\Leftarrow$ " auch eine strenge Version von [7.10.12/13]:

$f^{'}$ ist streng monoton steigend $\Rightarrow$ f ist streng konvex

${f^{'}}^{'} (x) > 0 für alle x \in I \Rightarrow$ f ist streng konvex

" $\Rightarrow$ " dagegen läßt sich nicht übertragen.

[7.10.7] zeichnet Punkte, die im Übergang zweier Monotoniebereiche liegen, besonders aus. Ähnlich interessant sind Punkte, in denen die Krümmungsrichtung wechselt.

Definition: $a \in I$ sei ein innerer Punkt von I. Eine Funktion $f : I \to ℝ$ besitzt in a einen Wendepunkt, falls es ein $ε > 0$ gibt, so dass f auf den Halbumgebungen

I \cap] a - ε, a]

und

I \cap [a, a + ε [

[7.10.14]

ein unterschiedliches Krümmungsverhalten hat. a nennen wir in diesem Fall eine Wendestelle von f.

Wir nennen den Wendepunkt $(a, f (a))$ auch einen Sattelpunkt, falls f zusätzlich in a differenzierbar ist mit $f^{'} (a) = 0$ . Sattelpunkte sind also Wendepunkte mit waagerechter Tangente.

Beachte:

Da eine lineare Funktion gleichzeitig konvex und konkav ist, wechselt sie an jeder Stelle ihre Krümmungsrichtung. Lineare Funktionen besitzen daher in jedem $x \in ℝ$ einen Wendepunkt.
Nach [7.10.12] gilt für $D^{1}$ -Funktionen:

f besitzt einen Wendepunkt in a $\Leftrightarrow f^{'}$ ändert in a das Monotonieverhalten.[6]
Nach [7.10.13] gilt für $D^{2}$ -Funktionen:

f besitzt einen Wendepunkt in a $\Leftrightarrow {f^{'}}^{'}$ wechselt in a das Vorzeichen.[7]

Mit [6] und [7] lassen sich leicht notwendige Kriterien für die Existenz von Wendestellen notieren.

Bemerkung: Besitzt $f : I \to ℝ$ in $a \in I$ einen Wendepunkt, so gilt für eine

$D^{1}$ -Funktion:

f^{'}

besitzt in a ein lokales Extremum.

[7.10.15]

$D^{2}$ -Funktion:

{f^{'}}^{'} (a) = 0

[7.10.16]

In beiden Fällen ist die Umkehrung i.A. falsch.

Beweis:

1. ► Gemäß [6] ändert $f^{'}$ in a das Monotonieverhalten und besitzt daher nach [7.10.7] ein lokales Extremum in a.

Wir benötigen ein Gegenbeispiel, um zu zeigen, dass die Umkehrung nicht gültig ist. Dazu betrachten wir noch einmal die in [7.10.8] eingeführte differenzierbare, also auch stetige Funktion $f : ℝ \to ℝ$ gegeben durch

f (x) ≔ {\begin{array}{l} 0,  falls x = 0 \\ (x \cdot \sin x^{- 1})^{2},  falls x \neq 0 \end{array}

Da f stetig ist, gibt es nach [8.1.5] eine differenzierbare Funktion $g : ℝ \to ℝ$ mit $g^{'} = f$ . Die in [7.10.8] nachgewiesenen Eigenschaften von f lesen wir jetzt so:

$g^{'}$ besitzt in 0 ein globales Minimum.
${g^{'}}^{'}$ wechselt in 0 nicht das Vorzeichen, g hat also nach [7] keinen Wendepunkt in 0.

2. ► ist aufgrund von 1. eine direkte Folgerung aus [7.9.2].

Die nicht-konstante Funktion $X^{4}$ ist gemäß [7.10.13] auf ganz $ℝ$ konvex ( $(X^{4} {)^{'}}^{'} (x) = 12 x^{2} \geq 0$ für alle x! ), besitzt also keinen Wendepunkt. Dennoch ist $(X^{4} {)^{'}}^{'} (0) = 0$ .

Für $C^{n + 2}$ -Funktionen erhalten wir ein hinreichendes Kriterium mit Hilfe der Taylorformel [7.9.16]. Wir gehen dabei parallel zu [7.9.17] vor.

Bemerkung (hinreichendes Kriterium für $\underline{C^{n + 2}}$ -Funktionen): Sei $f \in C^{n + 2} (I)$ und a ein innerer Punkt von I, so dass

{f^{'}}^{'} (a) = \dots = f^{(n + 1)} (a) = 0 \land f^{(n + 2)} (a) \neq 0

[7.10.17]

Ist n + 2 ungerade, so besitzt f in a einen Wendepunkt.
Ist n + 2 gerade, so besitzt f in a keinen Wendepunkt.

Beweis: Wir wenden die Taylorformel auf die $C^{n}$ -Funktion ${f^{'}}^{'}$ an. Sei o.E. etwa ${f^{'}}^{'} (a) > 0$ . Mit einem Stetigkeitsargument findet man ein $ε > 0$ , so dass ${f^{'}}^{'} (x) > 0$ für alle $x \in I_{a, ε}$ . Zu jedem x dieser Art gibt es nun ein $\tilde{x}$ zwischen x und a, so dass

{f^{'}}^{'} (x) = \sum_{i = 0}^{n - 1} \frac{f^{(i + 2)} (a)}{i!} {(x - a)}^{i} + \frac{f^{(n + 2)} (\tilde{x})}{n!} {(x - a)}^{n} = \underset{> 0}{\underset{︸}{\frac{f^{(n + 2)} (\tilde{x})}{n!}}} {(x - a)}^{n}

${f^{'}}^{'}$ wechselt also genau dann das Vorzeichen in a wenn n ungerade ist. Gemäß [7] ist dies die Behauptung.

Beachte:

Für eine $C^{3}$ -Funktion erhält man das bekannte Ergebnis:

${f^{'}}^{'} (a) = 0 \land {f^{'}}^{'}^{'} (a) \neq 0 \Rightarrow$ f besitzt in a einen Wendepunkt.

Die Eigenschaften "konvex" und "konkav" ermöglichen es, bei einer Funktion die Art der Krümmung - links- oder rechtsgekrümmt - zu untersuchen. Dies führt zu einer rein qualitativen Aussage. Eine quantitative Messung, wie groß oder wie klein die Krümmung an einer bestimmten Stelle ist, ist damit allerdings damit nicht verbunden.

Messbare Krümmungsverhältnisse kennen wir bislang nur von Kreisen: Hier nämlich ist mit dem Radius ein Wert gegeben, den man zur Messung der Krümmung einsetzen kann. Da allerdings die Krümmung um so kleiner ausfällt, je größer der Radius ist, werden wir als psychologisch richtiges Maß den Kehrwert des Radius als Krümmungsmaß einrichten.

Wenn es nun gelingt einen Kreis, den sog. Krümmungskreis zu finden, der sich einer gegebenen Funktion f an einer geeigneten Stelle a optimal anschmiegt, so können wir seinen Radius als den Krümmungsradius von f in a ansprechen.

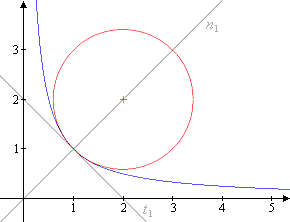
Die nebenstehende Skizze zeigt den Krümmungskreis zur Kehrwertfunktion $\frac{1}{X}$ in 1. Der Abstand seines Mittelpunkts (2,2) zum Berührpunkt (1,1) liefert hier den Krümmungsradius $\sqrt{2}$ .

Wie aber konstruiert man einen solchen optimalen Kreis, seinen Mittelpunkt und seinen Radius also? Zunächst wird man erwarten, dass der Krümmungskreis die Funktion "senkrecht berührt". Wir suchen daher einen Kreis, der durch den Punkt (a, f(a)) geht und dessen Mittelpunkt auf der Normalen $n_{a}$ , also der Senkrechten zur Tangente $t_{a}$ , liegt.

Welcher dieser Kreise nun der "richtige" ist, muss durch die lokale Geometrie der Kurve, d.h. durch die Funktionswerte in der Nähe von a bestimmt sein. Analog zur Konstruktion der Tangente (dort hatten wir zunächst durch Zugriff auf weitere Punkte (x, f(x)) Sekanten als Hilfsobjekte eingeführt) werden wir "Sekantenkreise" betrachten, Kreise also, die zusätzlich durch Punkte der Form (x, f(x)) gehen. Ihren Mittelpunkt erhält man dann als Schnitt der Normalen mit der Mittelsenkrechten, die zu der durch x gegebenen Sekante gehört. Das nachstehende Applet illustriert dieses Konzept.

Wir untersuchen im Folgenden $C^{2}$ -Funktionen in solchen Stellen a, an denen eine eindeutige Krümmungsrichtung vorliegt. Da dies in Wendepunkten nicht der Fall ist, werden wir ${f^{'}}^{'} (a) \neq 0$ verlangen. Außerdem ist es hier deutlich günstiger, die vektorielle Schreibweise zu benutzen. Wir notieren also die Tangente, die Normale und die Mittelsenkrechte in der Form

\begin{array}{l} t_{a} = (\begin{matrix} a \\ f (a) \end{matrix}) + < (\begin{matrix} 1 \\ f^{'} (a) \end{matrix}) > \\ n_{a} = (\begin{matrix} a \\ f (a) \end{matrix}) + < (\begin{matrix} f^{'} (a) \\ - 1 \end{matrix}) > \\ s_{x} = \frac{1}{2} (\begin{matrix} x + a \\ f (x) + f (a) \end{matrix}) + < (\begin{matrix} f (x) - f (a) \\ - (x - a) \end{matrix}) > \end{array}

Bemerkung: Sei $f \in C^{2} (I)$ und a ein innerer Punkt von I. Ist ${f^{'}}^{'} (a) \neq 0$ , so gibt es o.E. zu jedem $x \in I \ {a}$ Punkte $\tilde{x}, \tilde{\tilde{x}}$ zwischen x und a, so dass sich die Geraden $n_{a}$ und $s_{x}$ im Punkt

$M_{a} (x) ≔ \frac{1}{2} (\begin{matrix} x + a \\ f (x) + f (a) \end{matrix}) - \frac{1 + f^{'} (a) f^{'} (\tilde{x})}{{f^{'}}^{'} (\tilde{\tilde{x}})} (\begin{matrix} \frac{f (x) - f (a)}{x - a} \\ - 1 \end{matrix})$
[7.10.18]

schneiden. $M_{a} (x)$ ist ihr einziger Schnittpunkt.

Beweis: Die Stetigkeit von ${f^{'}}^{'}$ garantiert, dass ${f^{'}}^{'} (x) \neq 0$ für alle x aus einer Umgebung $I_{a, ε}$ von a. Ohne Einschränkung nehmen wir an, dass $I_{a, ε} = I$ ist.

Wir berechnen den Schnitt der beiden Geraden nach der im Abschnitt 9.9 dargestellten Methode. Für einen Vektor

$\vec{z} = \frac{1}{2} (\begin{matrix} x + a \\ f (x) + f (a) \end{matrix}) + α (\begin{matrix} f (x) - f (a) \\ a - x \end{matrix}) \in s_{x}$

hat man danach:

$\begin{array}{l} \vec{z} \in n_{a} & \Leftrightarrow (\begin{matrix} f^{'} (a) \\ - 1 \end{matrix}) \vec{y} = (\begin{matrix} \frac{x + a}{2} - a + α (f (x) - f (a)) \\ \frac{f (x) + f (a)}{2} - f (a) + α (a - x) \end{matrix}) ist lösbar \\ \underset{I + f^{'} (a) II}{\Leftrightarrow} (\begin{matrix} 0 \\ - 1 \end{matrix}) \vec{y} = (\begin{matrix} \frac{x - a}{2} + α (f (x) - f (a)) + f^{'} (a) (\frac{f (x) - f (a)}{2} + α (a - x)) \\ \frac{f (x) - f (a)}{2} + α (a - x) \end{matrix}) ist lösbar \\ \Leftrightarrow α (f (x) - f (a) + f^{'} (a) (a - x)) + \frac{x - a}{2} + f^{'} (a) \frac{f (x) - f (a)}{2} = 0 [ 8 ] \end{array}$

Mit dem Taylorsatz [7.9.16] finden wir jetzt zwei Punkte $\tilde{x}, \tilde{\tilde{x}}$ zwischen x und a, so dass

$f (x) - f (a) = f^{'} (\tilde{x}) (x - a)$

$f (x) - f (a) - f^{'} (a) (x - a) = \frac{1}{2} {f^{'}}^{'} (\tilde{\tilde{x}}) {(x - a)}^{2}$

Wir können daher [8] äquivalent weiterschreiben zu

$\begin{array}{l} α \frac{1}{2} {f^{'}}^{'} (\tilde{\tilde{x}}) {(x - a)}^{2} + \frac{x - a}{2} + f^{'} (a) \frac{f^{'} (\tilde{x}) (x - a)}{2} = 0 \\ \Leftrightarrow & α {f^{'}}^{'} (\tilde{\tilde{x}}) (x - a) + 1 + f^{'} (a) f^{'} (\tilde{x}) = 0 \\ \Leftrightarrow & α = - \frac{1 + f^{'} (a) f^{'} (\tilde{x})}{{f^{'}}^{'} (\tilde{\tilde{x}}) (x - a)}, \end{array}$

so dass sich

$\begin{array}{l} \vec{z} & = \frac{1}{2} (\begin{matrix} x + a \\ f (x) + f (a) \end{matrix}) - \frac{1 + f^{'} (a) f^{'} (\tilde{x})}{{f^{'}}^{'} (\tilde{\tilde{x}}) (x - a)} (\begin{matrix} f (x) - f (a) \\ a - x \end{matrix}) \\ = \frac{1}{2} (\begin{matrix} x + a \\ f (x) + f (a) \end{matrix}) - \frac{1 + f^{'} (a) f^{'} (\tilde{x})}{{f^{'}}^{'} (\tilde{\tilde{x}})} (\begin{matrix} \frac{f (x) - f (a)}{x - a} \\ - 1 \end{matrix}) \end{array}$

als einziger Lösungsvektor ergibt.

Mit den Schnittpunkten $M_{a} (x)$ stehen uns jetzt die Mittelpunkte der Sekantenkreise zur Verfügung, so dass wir ihr Grenzwertverhalten untersuchen können. Läuft x gegen a, so muss dies auch auf $\tilde{x}$ und $\tilde{\tilde{x}}$ zutreffen. Da nun f in a differenzierbar ist und $f, f^{'}, {f^{'}}^{'}$ dort stetig sind, besitzt $M_{a}$ einen Grenzwert in a, und zwar:

$\lim_{x \to a} M_{a} (x) = (\begin{matrix} a \\ f (a) \end{matrix}) - \frac{1 + {(f^{'} (a))}^{2}}{{f^{'}}^{'} (a)} (\begin{matrix} f^{'} (a) \\ - 1 \end{matrix})$ .

Dieser Grenzwert liegt offensichtlich auf der Normalen $n_{a}$ . Seinen Abstand zum Berührpunkt (a, f(a)) berechnen wir zu

$| \lim_{x \to a} M_{a} (x) - (\begin{matrix} a \\ f (a) \end{matrix}) | = | \frac{1 + {(f^{'} (a))}^{2}}{{f^{'}}^{'} (a)} | \cdot | (\begin{matrix} f^{'} (a) \\ - 1 \end{matrix}) | = | \frac{1 + {(f^{'} (a))}^{2}}{{f^{'}}^{'} (a)} | \sqrt{1 + {(f^{'} (a))}^{2}}$ .

Damit haben wir unser Ziel erreicht: Wir können Krümmungsverhältnisse quantitativ beschreiben!

Definition: Ist $f \in C^{2} (I)$ und a ein innerer Punkt von I mit ${f^{'}}^{'} (a) \neq 0$ , so nennen wir den durch seinen

Krümmungsmittelpunkt $M (a) ≔ (\begin{matrix} a \\ f (a) \end{matrix}) - \frac{1 + {(f^{'} (a))}^{2}}{{f^{'}}^{'} (a)} (\begin{matrix} f^{'} (a) \\ - 1 \end{matrix})$
[7.10.19]

und seinen

Krümmungsradius $r (a) ≔ \frac{{\sqrt{1 + {(f^{'} (a))}^{2}}}^{3}}{| {f^{'}}^{'} (a) |}$
[7.10.20]

gegeben Kreis den zu f gehörigen Krümmungskreis bzgl. a. Die Zahl $k (a) = \frac{1}{r (a)} = \frac{| {f^{'}}^{'} (a) |}{{\sqrt{1 + {(f^{'} (a))}^{2}}}^{3}}$ heißt die Krümmung von f in a.

Im Fall ${f^{'}}^{'} (a) = 0$ setzen wir zusätzlich $r (a) ≔ \infty$ und $k (a) ≔ 0$ .

Als Beispiel ermitteln wir die Krümmungsdaten der Normalparabel und die eines Halbkreises um den Koordinatenursprung mit Radius r. Hier erwarten wir, dass alle Krümmungsradien mit r, und alle Mittelpunkte mit (0,0) übereinstimmen.

Beispiel:

Für $f = X^{2}, f^{'} = 2 X, {f^{'}}^{'} = 2 und a \in ℝ$ errechnen wir:

$M (a) = (\begin{matrix} a \\ a^{2} \end{matrix}) - \frac{1 + 4 a^{2}}{2} (\begin{matrix} 2 a \\ - 1 \end{matrix}) = (\begin{matrix} - 4 a^{3} \\ \frac{1}{2} + 3 a^{2} \end{matrix})$

$r (a) = \frac{{\sqrt{1 + 4 a^{2}}}^{3}}{2}$

$k (a) = \frac{2}{{\sqrt{1 + 4 a^{2}}}^{3}}$

Für $f = \sqrt{r^{2} - X^{2}}, f^{'} = - \frac{X}{\sqrt{r^{2} - X^{2}}}, {f^{'}}^{'} = - \frac{r^{2}}{{\sqrt{r^{2} - X^{2}}}^{3}} und a \in] - r, r [$ ist zunächst

$\frac{1 + \frac{a^{2}}{r^{2} - a^{2}}}{- \frac{r^{2}}{{\sqrt{r^{2} - a^{2}}}^{3}}} = - \frac{{\sqrt{r^{2} - a^{2}}}^{3} + a^{2} \sqrt{r^{2} - a^{2}}}{r^{2}} = - \sqrt{r^{2} - a^{2}} \frac{{\sqrt{r^{2} - a^{2}}}^{2} + a^{2}}{r^{2}} = - \sqrt{r^{2} - a^{2}}$ .

Damit erhalten wir:

$M (a) = (\begin{matrix} a \\ \sqrt{r^{2} - a^{2}} \end{matrix}) + \sqrt{r^{2} - a^{2}} (\begin{matrix} - \frac{a}{\sqrt{r^{2} - a^{2}}} \\ - 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})$

$r (a) = \frac{{\sqrt{1 + \frac{a^{2}}{r^{2} - a^{2}}}}^{3}}{\frac{r^{2}}{{\sqrt{r^{2} - a^{2}}}^{3}}} = \frac{{\sqrt{r^{2} - a^{2} + a^{2}}}^{3}}{r^{2}} = r$

$k (a) = \frac{1}{r}$

7.9. 7.11.