6.9. Eigenschaften stetig fortsetzbarer Funktionen
Naturgemäß erben stetig fortsetzbare Funktionen etliche Eigenschaften von den stetigen Funktionen. Aber auch zu einigen Sätzen über Folgen gibt es hier entsprechende Varianten, etwa zum Schachtelsatz sowie zu den Grenzwertsätzen.
Zunächst weisen wir, wie bei den stetigen Funktionen auch, auf den lokalen Charakter der stetigen Fortsetzbarkeit hin.
|
Bemerkung: Es sei a ein Häufungspunkt von . Ist in a stetig fortsetzbar, so ist auch stetig fortsetzbar in a und:
|
[6.9.1] |
Die Umkehrung ist i.a. falsch.
Beweis: Ist eine stetige Fortsetzung von f in a, so ist gemäß [6.2.8]
die stetige Fortsetzung von in a. Die Gleichheit der Grenzwerte ist damit ebenfalls gegeben.
Die
Heavisidefunktion H
i  |
|
|
ist in 0 nicht stetig fortsetzbar, wohl aber ihre Einschränkung .
|
Lokal identische Funktionen unterscheiden sich nicht in ihrem Grenzwertverhalten (vergleiche dazu [6.2.11]). Auch dies zeigt, dass die stetige Fortsetzbarkeit eine lokale Eigenschaft ist.
|
Bemerkung: a sei ein Häufungspunkt von . Sind und in a lokal identisch, so gilt:
f stetig fortsetzbar in ag stetig fortsetzbar in a
|
[6.9.2] |
Sind beide Funktionen stetig fortsetzbar, so hat man:
Beweis: Nach Voraussetzung gibt es relative -Umgebungen

i  |
|
|
und , so dass
und [0]
Es reicht, nur eine der beiden Richtungen, etwa "", zu zeigen. Wir setzen dabei das Folgenkriterium [6.8.4] ein.
Sei f stetig fortsetzbar in a. Ist eine Folge in B mit , so gibt es ein , so dass für alle . Für diese n hat man dann wegen [0]
und damit die Behauptung.
|
Beachte:
Parallel zu [6.2.11] erhalten wir für einen Häufungspunkt a von A durch Spezialisierung
f ist in a stetig fortsetzbar ist stetig fortsetzbar in a für ein
wobei im Fall der Fortsetzbarkeit die Grenzwerte übereinstimmen: .
Das Zusammenspiel zwischen einem Funktionswert und seinen Nachbarwerten (siehe [6.4.1] und [6.4.9]) ist auch für stetig fortsetzbare Funktionen formulierbar. Wir notieren hier ebenfalls nur die -Variante.
|
Bemerkung: sei in einem Häufungspunkt a von stetig fortsetzbar. Dann gilt für jedes und für jede relative -Umgebung :
-
Ist ,
so gibt es ein , derart dass für alle .
|
[6.9.3] |
-
Ist für alle , so ist .
|
[6.9.4] |
Beweis: Sei g stetige Fortsetzung von f in a.
1. ► Mit ergibt sich dann die Behauptung direkt aus [6.4.1].
2. ► Hier folgt der Beweis aus [6.4.9], denn für alle ist .
|
Zur Berechnung von Grenzwerten stehen uns, wie bei den Folgen auch, Grenzwertsätze als hilfreiches Instrument zur Verfügung.
|
Bemerkung (Grenzwertsätze): und seien zwei beliebige Funktionen, a ein Häufungspunkt von (also auch von A bzw. B). Sind f und g in a stetig fortsetzbar, so gilt dies auch für
-
und
|
[6.9.5] |
-
und
|
[6.9.6] |
-
und
|
[6.9.7] |
-
und , falls
|
[6.9.8] |
Beweis: Nach Voraussetzung gibt es in a stetige Fortsetzungen zu f und zu g, etwa
1. ► Dann aber ist die stetige Fortsetzung von in a. Ihren Grenzwert können wir daher folgendermaßen errechnen:
2./3. ► Der Beweis ist i.w. eine Kopie der gerade geführten Überlegung.
4. ► Der Formelanteil ergibt sich wieder wie zuvor. Allerdings muss jetzt noch gepüft werden, ob a auch ein Häufungspunkt von ist:
Da a Häufungspunkt von ist, gibt es zunächst eine Folge in , die gegen a konvergiert, und da , gibt es aus Stetigkeitsgründen (siehe [6.4.2]) eine relative -Umgebung von a, so dass
Ab einem geeigneten liegen aber alle Folgenglieder in . Daher ist eine gegen a konvergente Folge in .
|
Die Komposition zweier Funktionen verträgt sich ebenfalls mit der stetigen Fortsetzbarkeit.
|
Bemerkung: und seien zwei Funktionen, a ein Häufungspunkt von . Ist g stetig fortsetzbar in a und ein Häufungspunkt von B in dem f stetig fortsetzbar ist, so ist auch in a stetig fortsetzbar und
|
[6.9.9] |
Beweis: Wir setzen das Folgenkriterium [6.8.4] ein: Ist eine Folge in mit , so hat man der Reihe nach:
-
, denn g ist in a stetig fortsetzbar
-
, denn f ist in stetig forstsetzbar
|
Neben den rechnerischen Möglichkeiten einen Grenzwert zu ermitteln, benötigt man auch abschätzende Verfahren, wie etwa den Schachtelsatz.
|
Bemerkung (Schachtelsatz): a sei ein Häufungspunkt von A und drei Funktionen, so dass
.
Sind f und h in a stetig fortsetzbar mit , so ist auch g dort stetig fortsetzbar und
|
[6.9.10] |
Beweis: Wir arbeiten wieder mit dem Folgenkriterium [6.8.4] und geben dazu eine Folge in A vor, die gegen a konvergiert. Die Voraussetzungen liefern
so dass sich die Behauptung direkt aus dem Schachtelsatz für Folgen [5.5.8] ergibt.
|
Oft setzt man den Schachtelsatz ein, nachdem man eine Differenz dem Betrage nach abgeschätzt hat. Die folgende Bemerkung stellt sicher, dass damit Grenzwerte ermittelt werden können.
|
Bemerkung: sei irgendeine Funktion, a ein Häufungspunkt von und . Dann sind die folgenden Aussagen äquivalent:
|
|
f ist in a stetig fortsetzbar und
|
[6.9.11] |
|
|
ist in a stetig fortsetzbar und |
Beweis: Die Richtung "" ergibt sich direkt aus den Rechenregeln [6.9.6] und [6.9.9]. Die zweite Richtung "" zeigen wir mit dem Folgenkriterium:
|
|
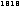 |
|