5.5. Eigenschaften konvergenter Folgen

Wir untersuchen zunächst, ob die Konvergenz einer Folge Aussagen über ihre Monotonie bzw. ihre Beschränktheit zuläßt. Da es unter den konvergenten Folgen sowohl monotone wie auch nicht-monotone gibt, und unter den divergenten ebenfalls, besteht zwischen der Monotonie und der Konvergenz kein Zusammenhang. Ein wenig besser verhält sich dagegen die Beschränktheit zur Konvergenz: Zwar gibt es divergente Folgen, die beschränkt sind, wie etwa

({(- 1)}^{n})

, aber aus der Konvergenz folgt stets die Beschränktheit.

Bemerkung:

Jede konvergente Folge ist beschränkt.

[5.5.1]

Beweis: Ist etwa $a_{n} \to g$ , so gibt es gemäß [5.4.2] insbesondere zu 1 ein $n_{0} \in ℕ^{*}$ , so dass

g - 1 < a_{n} < g + 1 für alle n \geq n_{0}

Damit hat man aber für alle $n \in ℕ^{*}$ :

\min {g - 1, a_{1}, \dots, a_{n_{0} - 1}} \leq a_{n} \leq \max {g + 1, a_{1}, \dots, a_{n_{0} - 1}}

Als eine Folgerung ergibt sich ein neues Kriterium für die Divergenz einer Folge:

Unbeschränkte Folgen sind stets divergent.

Die Divergenz von $(n)$ etwa, läßt sich also auch durch ihre Unbeschränktheit erklären.

Zwei weitere Eigenschaften beleuchten das Zusammenspiel zwischen der Lage der Folgenglieder und der des Grenzwerts:

Bemerkung: Es sei $a_{n} \to g$ . Dann gilt für jedes $c \in ℝ$ :

$g > c \Rightarrow a_{n} > c$ für alle n ab einem geeignetem $n_{0}$

$g < c \Rightarrow a_{n} < c$ für alle n ab einem geeignetem $n_{0}$

[5.5.2]

$a_{n} \geq c für alle n \Rightarrow g \geq c$

$a_{n} \leq c für alle n \Rightarrow g \leq c$

[5.5.3]

Beweis: Wir zeigen jeweils nur die erste Variante.

1. ►
Sei $g > c$ , also $r ≔ g - c > 0$ . Da $a_{n} \to g$ , liegen in der speziellen $ε$ -Umgebung $] g - r, g + r [$ ab einem $n_{0}$ alle Folgenglieder. D.h. insbesondere
$a_{n} > g - r = g - (g - c) = c für alle n \geq n_{0} .$

2. ►
Wir gehen indirekt vor und nehmen an: $g < c$ . Nach 1. ist dann aber $a_{n} < c$ für fast alle n im Widerspruch zu $a_{n} \geq c$ für alle n.

Beachte:

1. benutzt man oft, und zwar insbesondere für $c = 0$ , in der folgenden Form:

$g \neq c \Rightarrow a_{n} \neq c$ für alle n ab einem geeigneten $n_{0}$
[5.5.4]

Wie das Beispiel $0 < \frac{1}{n} \to 0$ zeigt, läßt sich 2. nicht verschärfen indem man etwa $\geq$ durch $>$ ersetzt.
Wegen $a_{n} \to g \Leftrightarrow a_{n + k} \to g$ darf man allerdings in 2. die Voraussetzung durch die Formulierung "für fast alle n" abschwächen.

Die beiden Aussagen in 2. kann man offensichtlich kombinieren zu:

$a_{n} \in [a, b] für fast alle n \Rightarrow g \in [a, b]$
[5.5.5]

Bei Konvergenzuntersuchungen von Nullfolgen darf man sich auf positive Folgen beschränken. Das ist oftmals eine angenehme technische Erleichterung:

Bemerkung: Es sei $(a_{n})$ irgendeine Folge. Dann gilt:

a_{n} \to 0 \Leftrightarrow | a_{n} | \to 0

[5.5.6]

Beweis: Aus der Gleichheit $| a_{n} - 0 | = | a_{n} | = | | a_{n} | - 0 |$ erhält man für jedes $ε > 0$ :

| a_{n} - 0 | < ε \Leftrightarrow | | a_{n} | - 0 | < ε

und daraus unmittelbar die Behauptung.

Als Beispiel untersuchen wir die Folge $(\frac{{(- 1)}^{n}}{n})$ . Da $| \frac{{(- 1)}^{n}}{n} | = \frac{1}{n} \to 0$ folgt:

\frac{{(- 1)}^{n}}{n} \to 0

Die Glieder einer konvergenten Folge kommen dem Grenzwert beliebig nah. Das hat Konsequenzen auf die Beziehung der Folgenglieder untereinander: Auch sie müssen beliebig nah aneinander rücken. Die in der folgenden Bemerkung genannte Eigenschaft nennt man auch die Cauchy-Bedingung.

Bemerkung: Ist $a_{n} \to g$ , so gibt es zu jedem $ε > 0$ ein $n_{0} \in ℕ^{*}$ , so dass

| a_{n} - a_{m} | < ε für alle n, m \geq n_{0}

[5.5.7]

Beweis: Zunächst findet man auf Grund der Konvergenz ein $n_{0} \in ℕ^{*}$ , so dass

| a_{n} - g | < \frac{ε}{2} für alle n \geq n_{0} .

Für $n, m \geq n_{0}$ hat man daher nach Dreiecksungleichung die folgende Abschätzung:

| a_{n} - a_{m} | = | a_{n} - g + g - a_{m} | \leq | a_{n} - g | + | a_{m} - g | < \frac{ε}{2} + \frac{ε}{2} = ε

Ein interessante Frage ist, ob die Cauchy-Bedingung die Konvergenz bereits erzwingt. Im Allgemeinen ist dies falsch. So gibt es in $ℚ$ divergente Folgen, die die Cauchy-Bedingung erfüllen! In $ℝ$ jedoch liegen besondere Verhältnisse vor; und hier sind tatsächlich Cauchy-Folgen auch bereits konvergent wie wir im Abschnitt 8 sehen werden.

Wir beschließen diesen Abschnitt mit dem Schachtelsatz, einem Konvergenzkriterium, das bei manchen "schwierigen" Folgen gut eingesetzt werden kann.

Bemerkung (Schachtelsatz): $(a_{n})$ , $(b_{n})$ und $(c_{n})$ seien drei Folgen, so dass

a_{n} \leq b_{n} \leq c_{n} für alle n \in ℕ^{*}

Sind $(a_{n})$ und $(c_{n})$ konvergent gegen denselben Grenzwert g, also $a_{n} \to g$ und $c_{n} \to g$ , so konvergiert $(b_{n})$ ebenfalls gegen g:

b_{n} \to g

[5.5.8]

Beweis: Wir arbeiten mit dem Konvergenzkriterium [5.4.2]. Sei $ε > 0$ vorgegeben. Da $a_{n} \to g$ , gibt es ein $n_{1} \in ℕ^{*}$ , so dass

g - ε < a_{n} < g + ε für alle n \geq n_{1} .

Ebenso findet man ein $n_{2} \in ℕ^{*}$ , derart dass

g - ε < c_{n} < g + ε für alle n \geq n_{2} .

Für alle $n \geq n_{0} ≔ \max {n_{1}, n_{2}}$ gilt daher der Reihe nach:

g - ε < a_{n} \leq b_{n} \leq c_{n} < g + ε

g - ε < b_{n} < g + ε

Also ist die Konvergenz $b_{n} \to g$ sicher gestellt.

Beachte:

"Wie üblich" darf man die Voraussetzung abschwächen zu: $a_{n} \leq b_{n} \leq c_{n}$ für fast alle n.

Beispiel:

\frac{\sin n}{n} \to 0

[5.5.9]

Beweis: Da alle Sinuswerte zwischen −1 und 1 liegen, hat man für alle n die folgende Abschätzung; mit den angegebenen Konvergenzen folgt dann die Behauptung aus dem Schachtelsatz.

\begin{matrix} \underset{↓}{- \frac{1}{n}} & \leq \frac{\sin n}{n} \leq & \underset{↓}{\frac{1}{n}} \\ 0 & 0 \end{matrix}

Dieses Beispiel läßt sich leicht verallgemeinern, denn von $(\sin n)$ wurde im Prinzip nur die Beschränktheit und von $(\frac{1}{n})$ nur die Konvergenz gegen 0 ausgenutzt.

Bemerkung: Ist $(a_{n})$ beschränkt und $(b_{n})$ eine Nullfolge, so gilt:

a_{n} \cdot b_{n} \to 0

[5.5.10]

Beweis: Nach [5.5.6] reicht es zu zeigen: $| a_{n} \cdot b_{n} | \to 0$ . Da $(a_{n})$ beschränkt ist, gibt es ein $s \in ℝ^{> 0}$ , so dass $| a_{n} | \leq s$ für alle n. Also hat man:

0 \leq | a_{n} \cdot b_{n} | = | a_{n} | \cdot | b_{n} | \leq s \cdot | b_{n} |

Mit $(b_{n})$ ist gemäß [5.5.6] auch $(| b_{n} |)$ eine Nullfolge. Nach [5.6.5] hat man daher: $s \cdot | b_{n} | \to 0$ . Da außerdem $0 \to 0$ , folgt nun die Behauptung aus dem Schachtelsatz.

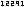5.4. 5.6.