5.4. Konvergente Folgen
Als Einführung zu diesem Abschnitt betrachten wir die
Folge , eine unserer ersten Beispielfolgen. Ihre Wertetabelle rufen wir noch einmal ab
und achten dabei etwas genauer auf die Folgenglieder: Zunächst fällt
auf, dass jeder Zähler fast doppelt so groß ist wie der
zugehörige Nenner, alle Folgenglieder sind somit kleiner als 2. Der
Unterschied zwischen dem Zweifachen des Nenners und dem Zähler ist aber
beständig 1, damit verkleinert sich der Abstand zwischen den Folgengliedern
und der Zahl 2 immer mehr.
Dies wird besonders deutlich, wenn man für die Folgenglieder die
Dezimaldarstellung verwendet und sie gleichzeitig auf dem Zahlenstrahl
markiert:
Auch rechnerisch läßt sich die Tendenz zu 2 erkennen, wenn man
den Abstand eines Folgengliedes zu 2 - also den Betrag der Differenz - ermittelt.
Für das 1000. Folgenglied etwa erhält man:
Das 1000. Folgenglied, und mit ihm alle weiteren, denn die Folgenglieder werden immer größer, ist also um weniger als 0.001 von 2 entfernt.
Um allerdings sicherzustellen, dass die Folge tatsächlich gegen
2 läuft, reicht es nicht, irgendwelche Folgenglieder zu wählen und deren Abstand
zu 2 als klein zu erkennen. Man muss statt dessen die Aufgabenstellung
umdrehen: Kann man bei einem beliebig vorgegebenen Maximalabstand nachweisen, dass nahezu alle
Folgenglieder um weniger als von 2 entfernt sind?
Bevor wir dies für unsere Beispielfolge sicherstellen, wird zunächst
in der folgenden Definition der anschaulich leicht zu verstehende Sachverhalt
"eine Folge läuft gegen eine Zahl g"
mathematisch präzisiert.
Diese Begriffsbestimmung ist die Grundlage der Analysis.
|
Definition: Es sei eine Folge und . Wir sagen konvergiert gegen g (in Zeichen: ) falls es zu jedem gibt, so dass
|
[5.4.1] |
Ist konvergent gegen g, so nennt man g einen Grenzwert, bzw. einen Limes von . Die Folge selbst heißt in diesem Fall konvergent. Folgen, die keinen Grenzwert besitzen nennt man divergent.
|
Beachte:
Es ist gelegentlich von Vorteil die Konvergenzbedingung umzuformulieren.
Die Forderung, der Abstand von zu g soll kleiner als sein, ist genau dann erfüllt, wenn höchstens
Einheiten von g entfernt liegt, und zwar
unabhängig davon, ob rechts oder links von g liegt. darf sich also nur in einem offenen Intervall mit g als Mittelpunkt und als Radius aufhalten:
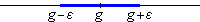
In diesem Zusammenhang nennen wir die auftretenden Mittelpunktsintervalle auch von g und notieren die Konvergenzbedingung folgendermaßen:
|
| zu jedem gibt es ein ,
so dass .
|
[5.4.2] |
Für unsere Eingangsfolge können wir nun die Konvergenz gegen 2 exakt nachweisen:
|
Beispiel:
-
Beweis: Sei vorgegeben. Wir haben ein zu finden, so dass die Folgenglieder von an aufwärts um weniger als von 2 entfernt sind. Wir machen uns zunächst klar, welche Anforderungen dies an die Folgenglieder stellt:
Damit ist klar: Haben die Folgenglieder einen Index der größer ist als , so ist ihre Entfernung zu 2 kleiner als .
Diese Information nutzen wir jetzt für die Wahl von aus: Da unbeschränkt ist (siehe [5.3.21]), können wir nämlich ein so wählen, dass . Dann gilt aber erst recht für alle .
Für diese n hat man daher
.
|
Beachte:
In Konvergenzbeweisen findet man oft die Aufforderung "Wähle jetzt ein ". Eine solche Wahl ist aber wegen der Unbeschränktheit von stets möglich! Es ist für zukünftige Nachweise bequem, dieses Argument stillschweigend vorauszusetzen.
Wenn auch die Konvergenz nun sicher gestellt ist, so ist die Frage ob noch weitere Grenzwerte besitzt durchaus zulässig,
denn die Konvergenzdefinition selbst gibt über die Eindeutigkeit des
Grenzwerts keine Auskunft. Man kann sich jedoch leicht davon überzeugen, dass eine Folge nicht zwei verschiedene Grenzwerte besitzen kann:
|
Bemerkung:
|
Jede Folge besitzt höchstens einen Grenzwert. |
[5.4.3] |
Beweis: Angenommen und sind zwei verschiedene Grenzwerte von . Dann ist ihr Abstand
größer als 0.
Legt man um und jeweils ein offenes Intervall mit dem Radius , so enthalten diese beiden -Umgebungen keine gemeinsamen Elemente. (+)

Da aber gibt es nach [5.4.2] ein , so dass alle Folgenglieder mit einem in der ersten Umgebung liegen müssen. Analog findet man alle Folgenglieder ab einem geeigneten in der zweiten Umgebung.
Setzt man nun , so gehört das Folgenglied zu beiden Umgebungen gleichzeitig, im Widerspruch zu (+).
|
Konvergente Folgen besitzen also genau einen Grenzwert!
Man darf daher ein Symbol einführen, das nur die Daten von benutzt. Ist , so sagt man g ist der Grenzwert von und schreibt:
, oder deutlicher: .
Die Konvergenz aus unserem Eingangsbeispiel kann man also auch so notieren:
.
Die Frage nach der Konvergenz einer Folge berührt immer auch das Problem der Divergenz. Aus unserer Alternative [5.4.2] gewinnen wir ein brauchbares Divergenzkriterium.
|
Bemerkung:
-
| in jeder -Umgebung von g fehlen höchstens endlich viele Folgenglieder.
|
[5.4.4] |
-
| es gibt eine -Umgebung von g in der unendlich viele Folgenglieder fehlen.
|
[5.4.5] |
Beweis:
|
1. ►
|
"": Ist eine beliebige -Umgebung von g, so gibt es nach [5.4.2] ein , so dass Damit können aber höchstens die Folgenglieder
- und das sind nur endlich viele - in fehlen.
"": Sei jetzt vorgegeben. Dann fehlen in höchstens endlich viele Folgenglieder, etwa . Setzt man nun , so müssen alle Folgenglieder mit zu gehören. Gemäß [5.4.2] ist damit die Konvergenz sichergestellt.
|
|
2. ►
|
Dies ist die Negation von 1.
|
|
Die folgenden Beispiele haben für die weitere Entwicklung eine zentrale Bedeutung. Im dritten Fall wird zudem das gerade vorgestellte
Kriterium für "nicht konvergent" benutzt.
|
Beispiel:
-
|
[5.4.6] |
|
Denn wählt man zu gegebenem ein , so gilt für alle und somit
.
|
-
für jede konstante Folge
|
[5.4.7] |
|
Denn ist vorgegeben, so gilt für alle
:
|
-
ist divergent
|
[5.4.8] |
|
Wir müssen zeigen: keine Zahl übernimmt die Rolle eines Grenzwertes von . Nun hat aber für jedes g die Menge unendliche viele Elemente, d.h. in
der speziellen -Umgebung fehlen unendlich viele Folgenglieder. Nach [5.4.2] bedeutet dies .
|
|
Die Divergenz der Folge liegt auch anschaulich auf
der Hand: Die natürlichen Zahlen "laufen nach rechts weg", können
sich also auf keine Stelle dauerhaft konzentrieren. Bei vielen Folgen ist
die Divergenz ähnlich begründet. Das folgende Beispiel allerdings
zeigt nun eine beschränkte Folge, die divergent ist. Hier tritt Divergenz ein, weil sich die Folge nicht für eine Stelle
entscheiden kann.
|
Beispiel:
ist divergent
|
[5.4.9] |
Beweis: Wir benutzen wieder das Kriterium [5.4.2].
In der speziellen -Umgebung
von 1 fehlen unendlich viele Folgenglieder, nämlich alle mit ungeradem Index, daher ist zunächst 1 kein Grenzwert von .
Ist nun g eine beliebige reelle Zahl ungleich 1, so ist . Da r der Abstand von g zu 1 ist, kann in die Zahl 1 nicht mehr enthalten sein. Also fehlen in dieser Umgebung ebenfalls unendlich viele Folgenglieder, und zwar alle mit geradem Index, so dass auch g nicht Grenzwert von ist.
Damit hat diese Folge überhaupt keinen Grenzwert, ist also divergent.
|
Die Konvergenz einer Folge beschreibt, wie sich die Folgenglieder "schließlich und endlich" verhalten. Darauf haben die ersten Folgenglieder natürlich keinen Einfluss, sie sind daher für das Konvergenzverhalten ohne Bedeutung.
Die folgende Bemerkung präzisiert diesen Sachverhalt.
|
Bemerkung: Es sei eine beliebige Folge. Dann gilt für jedes :
|
[5.4.10] |
Beweis:
"": Sei vorgegeben. Da , gibt es ein , so dass für alle . Da aber , gilt für diese n erst recht: . Also hat man .
"": Sei wieder vorgegeben. Da jetzt , gibt nun ein , so dass für alle . Für alle ist , also hat man: . Damit ist die Konvergenz bewiesen.
|
Konvergenznachweise - so haben es die bishierigen Beispiel gezeigt - bestehen im Kern stets darin, die Ungleichung nach n aufzulösen.
Dies kann allerdings bei komplizierteren Folgen sehr schnell zu einem nahezu unlösbaren Problem werden. Hilfreich ist jedoch die Tatsache, dass
es bei einem Konvergenznachweis nicht erforderlich ist, die genannte Ungleichung äquivalent aufzulösen; es reicht vielmehr, den Abstand durch eine Abschätzung unterhalb zu drücken.
Mit einem weiteren Konvergenzbeispiel soll diese Technik einmal beleuchtet werden.
Im nächsten Abschnitt werden deutlich bequemere Hilfsmittel
zur Verfügung gestellt, die in vielen Fällen einen Aufwand wie
den folgenden ersetzen können.
|
Beispiel:
-
Beweis: Sei vorgegeben. Wählt man ein , so gilt für alle
:
|
|
 |
|