6.10. Folgen stetiger Funktionen
In manchen Fällen ist es schwierig, Eigenschaften einer Funktion f direkt zu ermitteln. Oft gelingt dies aber, wenn man f durch leichter zu untersuchende Funktionen approximieren kann, wobei allerdings die zu untersuchende Eigenschaft mit der Approximationsmethode verträglich sein muss. In diesem Abschnitt stellen wir ein solches Konzept für die Stetigkeit vor.
|
Definition: Es sei . Ist für jedes eine Funktion mit , so nennen wir die Funktionenfolge punktweise konvergent auf A, falls für jedes die Zahlenfolge konvergiert. Die Funktion gegeben durch
|
[6.10.1] |
nennen wir die Grenzfunktion oder auch die Limesfunktion der Folge und schreiben . Die punktweise Konvergenz notieren wir in der Form
Ist stets , so lassen wir den Zusatz "auf A" in der Regel weg.
|
Beachte:
-
Da jeder Funktionswert als Grenzwert einer Zahlenfolge eindeutig bestimmt ist, kann auch eine Funktionenfolge nicht gegen zwei verschiedene Grenzfunktionen konvergieren.
-
Die Grenzfunktionen konvergenter Potenzreihen (siehe [5.11.9]) sind spezielle Beispiele für Limesfunktionen:
-
Wie bei gewöhnlichen Zahlenfolgen auch, hängt die punktweise Konvergenz nicht von den ersten Folgengliedern ab. Für jedes gilt nämlich:
|
Beispiel:
, denn: für jedes . ist auf nicht punktweise konvergent, da mindestens eine der Zahlenfolgen , hier etwa divergent ist. ist dagegen auf punktweise konvergent. Ihre Limesfunktion ist gegeben durch
|
[6.10.2] |
Beweis: Für weiß man gemäß [5.7.2]: , und ist offensichtlich.
|
Das letzte Beispiel offenbart einen Schwachpunkt der punktweisen Konvergenz: Obwohl alle Folgenglieder, also die Potenzen , auf stetig sind, ist die Grenzfunktion [6.10.2] dort
nicht stetig
i  |
|
und zwar nicht stetig in 1, denn , aber
.
|
. Ermöglicht wird ein solches Verhalten dadurch, dass die einzelnen Konvergenzen unkoordiniert sind: Zwar gibt des zu jedem ein , so dass
für alle , aber dieses kann von x zu x verschieden ausfallen. Erst mit einem schärferen Konvergenzbegriff können wir "Stetigkeitstreue" erreichen.
|
Definition: Eine Funktionenfolge heißt auf A gleichmäßig konvergent gegen eine Funktion , falls es zu jedem ein gibt, so dass
für alle und alle .
|
[6.10.3] |
f nennen wir wieder die Grenz- bzw. Limesfunktion und notieren die Konvergenz jetzt in der Form
.
Verbreitet ist hier auch die Schreibweise .
|
Beachte:
-
Ist gleichmäßig konvergent, so ist auch punktweise konvergent mit derselben Limesfunktion. Insbesondere ist daher die Grenzfunktion auch hier eindeutig bestimmt.
Die Umkehrung gilt nicht, wie das Beispiel [6.10.2] in Verbindung mit [6.10.5] zeigt. Für jedes gilt:
|
Beispiel:
Für jedes positive gilt:
|
|
Beweis: Ist vorgegeben, so gibt es nach [5.7.2] ein , so dass für alle und für alle gilt:
.
|
Der Beweis zu diesem Beispiel benutzt ein Verfahren, das wir in [6.10.7] zu einem Kriterium verallgemeinern. Zunächst jedoch zeigen wir, dass die gleichmäßige Konvergenz die Stetigkeit vererbt.
|
Bemerkung: Die Funktionenfolge sei auf A gleichmäßig konvergent und beliebig. Dann gilt für die Grenzfunktion f:
-
Ist jedes gleichmäßig stetig auf A, so ist auch f gleichmäßig stetig auf A.
|
[6.10.4] |
-
Ist jedes stetig in a, so ist auch f stetig in a.
|
[6.10.5] |
-
für alle n.
|
[6.10.6] |
Beweis:
1. ► Sei gegeben. Wir müssen ein finden (siehe [6.5.2]), so dass
für alle mit . Da , gibt es zunächst zu ein mit
für alle . [1]
Weil gleichmäßig stetig ist, gibt es jetzt ein , so dass
[2]
für alle mit . Für diese x gilt nun mit [1] und [2]:
2. ► Hier müssen wir zu ein finden (siehe [6.5.1]), so dass
für alle mit . Dies gelingt aber sofort mit dem Beweis zu 1, wenn wir dort y durch a ersetzen. Das Argument zu [2] ist dabei die Stetigkeit von in a.
3. ► ergibt sich direkt aus 2.
|
Es ist oft schwierig, die gleichmäßige Konvergenz einer Funktionenfolge nachzuweisen, so dass geeignete Kriterien sind höchst willkommen sind. Wir stellen zwei von ihnen vor: ein Majarantenkriterium und das bekannte Cauchy-Kriterium. Der technische Vorteil des Cauchy-Kriteriums ist es, dass man die Limesfunktion nicht vorher kennen muss, der Nachteil natürlich, dass die Limesfunktion auch nicht geliefert wird.
|
Bemerkung (Majorantenkriterium): Ist eine Funktionenfolge so gilt für :
|
|
es gibt eine Nullfolge in und ein , so dass
für alle und alle .
|
[6.10.7] |
Beweis:
"": Zunächst gibt es nach [6.10.3] zu 1 ein , so dass
für alle und alle .
Für ein solches n ist insbesondere die Menge nicht leer und beschränkt. Gemäß
Vollständigkeitsaxiom
i  |
|
Jede nicht-leere, beschränkte Teilmmenge von besitzt eine größte untere Schranke, ihr Infimum, und eine kleinste obere Schranke, ihr Supremum.
|
gibt es daher für jedes die Zahl
.
Wir setzen zusätzlich und haben damit eine Folge in konstruiert, die bereits [6.10.7] erfüllt. Bleibt also zu zeigen: . Sei dazu ein vorgegeben. Da gibt es ein , o.E. , so dass
für alle und alle .
Für diese n gilt daher: .
"": Da , gibt es zu jedem ein , o.E. , so dass
für alle und alle .
|
Als ein Beispiel betrachten wir die Folge . Für ein beliebiges konvergiert sie auf dem Intervall gleichmäßig gegen 0, denn die Abschätzung
für alle
weist als eine majorisierende Nullfolge aus.
|
Bemerkung (Cauchy-Kriterium): Eine Funktionenfolge ist auf A genau dann gleichmäßig konvergent, wenn es zu jedem ein gibt, so dass
für alle und alle .
|
[6.10.8] |
Beweis:
"": Der Beweis dieser Richtung ist eine direkte Kopie der entsprechenden Aussage [5.5.7] für gewöhnliche Folgen.
"": Für jedes ist eine reelle Cauchy-Folge, gemäß [5.8.8] also konvergent, so dass mit
[3]
eine Funktion gegeben ist. Wir zeigen jetzt: und geben dazu ein vor. Nach Voraussetzung findet man dann ein , so dass
für alle und alle . [4]
Für ein festes und ein beliebiges erhalten wir jetzt aus der Konvergenz [3] mit dem zweiten Grenzwertsatz, der Stetigkeit der Betragsfunktion und der Eigenschaft [5.5.3] gemäß [4] die folgende Abschätzung:
.
|
|
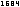 |
|