6.5. Gleichmäßig stetige Funktionen
In diesem Abschnitt zeigen wir, dass sich die Stetigkeit auch folgenfrei, durch die sog. -Notation, beschreiben läßt. Wir gewinnen dadurch die Möglichkeit, das Stetigkeitskonzept zu erweitern.
|
Bemerkung: sei eine beliebige Funktion, . Dann gilt:
|
f stetig in a
|
Zu jedem gibt es ein , so dass für alle gilt:
|
|
[6.5.1] |
Beweis:
"": Sei vorgegeben. Angenommen, es gibt kein der geforderten Art. Dann aber gibt es insbesondere zu jedem ein , so dass , aber . Damit hat man eine Folge in A gefunden, die gegen a konvergiert, deren Bildfolge aber nicht den Grenzwert hat. Widerspruch!
"": Sei nun eine Folge in A, die gegen a konvergiert. Wir müssen zeigen: . Dazu geben wir uns ein vor und finden gemäß Voraussetzung ein , so dass die Folgerung
[0]
für alle gültig ist. Da , hat man für alle n ab einem geeigneten . Gemäß [0] gilt daher für diese n:
|
Beachte:
Das in der -Formulierung verwandte Kriterium kann man auch so lesen: Zu jedem gibt es ein , so dass
D.h. zu jeder relativen -Umgebung gibt es eine relative -Umgebung , so dass
Oft ist eine Funktion in mehreren Punkten stetig. Leicht übersieht man dann, dass das in der -Formulierung garantierte Zusammenspiel zwischen einem vorgegebenem und einem zu findenden vom jeweiligen Punkt a abhängt, also nicht für alle a gleichmäßig wählbar ist. Durch den folgenden Begriff wird daher unser Stetigkeitskonzept verschärft.
|
Definition: Eine Funktion heißt auf gleichmäßig stetig, falls es zu jedem ein gibt, so dass
|
[6.5.2] |
|
Beachte: Dieser neue Stetigkeitsbegriff ist eine echte Verschärfung des alten, denn:
|
Bemerkung:
-
Ist f gleichmäßig stetig auf A, so ist f in jedem stetig.
|
[6.5.3]
|
-
Die stetige Funktion ist nicht gleichmäßig stetig auf .
|
[6.5.4]
|
Beweis:
1. ► Notiert man [6.5.2] für , so erhält man [6.5.1] als Spezialfall von [6.5.2].
2. ► Wir gehen indirekt vor und nehmen an, die Kehrwertfunktion sei gleichmäßig stetig. Dann gibt es zu ein , so dass für gilt:
Dabei dürfen wir annehmen. Wählt man nun ein positives und setzt , so erhält man den Widerspruch
|
In [6.5.4] belegt die Kehrwertfunktion, dass [6.5.3] i.a. nicht umkehrbar ist. Interessanterweise findet man aber unter den Funktionen auf einem abgeschlossenen Intervall keine Gegenbeispiele. Der folgende Satz ist bei vielen Abschätzungsaufgaben ein unentbehrliches Hilfsmittel.
|
Satz: Stetige Funktionen auf abgeschlossenen Intervallen sind gleichmäßig stetig:
f ist gleichmäßig stetig auf .
|
[6.5.5] |
Beweis: Sei vorgegeben. Wir gehen indirekt vor und nehmen an, es gäbe kein der geforderten Art, also erst recht kein der Form . Dann gibt es zu jedem Zahlen , so dass
[1]
Als beschränkte Folge besitzt nach dem Satz von Bolzano-Weierstraß ([5.8.6]) einen Häufungspunkt , den wir nach [5.8.5] als Grenzwert einer Teilfolge von , und damit als ein Element von gewinnen.
Da f in stetig ist, gibt es ein , so dass für alle gilt:
[2]
In der Umgebung liegen unendlich viele Glieder der Folge ( ist ja ein Häufungspunkt), sicherlich auch ein solches, dessen Index n die Abschätzung erfüllt. Für dieses n erhalten wir zunächst nach [1]:
und daher mit [2]
also einen Widerspruch zu [1].
|
Wie die Kehrwertfunktion in [6.5.4] zeigt, kann man bei diesem Satz auf die Abgeschlossenenheit des Intervalls nicht verzichten. Im nächsten Abschnitt werden wir sehen, dass sich die stetigen Funktionen auf abgeschlossenen Intervallen durch besondere Eigenschaften auszeichnen.
Diesen Teil schließen wir ab mit einer gelegentlich vorkommenden speziellen Form der gleichmäßigen Stetigkeit, der sog. Lipschitz-Stetigkeit:
|
Definition: Eine Funktion heißt auf lipschitz-stetig, falls es ein gibt, so dass
|
[6.5.6] |
|
Beachte:
Lipschitz-stetige Funktionen sind gleichmäßig stetig: Ist gegeben, so findet man in ein geeignetes .
Die Umkehrung ist i.a. falsch, denn die Wurzelfunktion etwa ist nach [6.5.5] auf gleichmäßig stetig, dort aber nicht lipschitz-stetig.
Wäre nämlich für ein die Abschätzung gültig für alle , so hätte man insbesondere für und :
Wählt man nun ein , also , so führt dies zum Widerspruch .
Besonders interessant sind lipschitz-stetige Funktionen, bei denen für den Stetigkeitsmodul c ein Wert unterhalb 1 gewählt werden kann. Dann nämlich liegen zwei Funktionswerte stets näher bei einander als ihre Urbilder und bei Funktionen, die geschlossene Intervalle auf sich abbilden, erzwingt dies die Existenz eines Fixpunktes:
|
Satz (Banachscher Fixpunktsatz): Läßt eine Funktion ein zu, so dass
,
so gibt es ein mit
|
[6.5.7] |
Beweis: Wir gehen konstruktiv vor und betrachten die Rekursion
Gemäß Voraussetzung ist die Abschätzung für jedes gültig und per Induktion erweiterbar zu
Für können wir damit unter Verwendung der Summenformel für die geometrische Reihe (siehe [5.2.4]) folgendermaßen abschätzen:
Da , ist eine Nullfolge (siehe [5.7.2]). Die gerade gewonnene Abschätzung für begründet daher, dass eine Cauchy-Folge, also (in ) konvergent ist. Für ihren Grenzwert hat man zunächst: und da f in stetig ist, gilt auch:
|
Beachte:
Der Fixpunkt in [6.5.7] ist eindeutig bestimmt. Wäre nämlich ein weiterer Fixpunkt aus , so führt die Information
zum Widerspruch .
Mit Hilfe des Banachschen Fixpunktsatzes lassen sich die Quadratwurzeln in elegant einführen. Für etwa zeigt die für gültige Abschätzung
dass durch die Vorschrift eine Funktion gegeben ist. f ist lipschitz-stetig mit , denn:
f besitzt also genau einen Fixpunkt . Damit aber gibt es in genau eine positive Zahl, deren Quadrat identisch mit a ist:
|
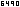 |
|