4.3. Die trigonometrischen Funktionen
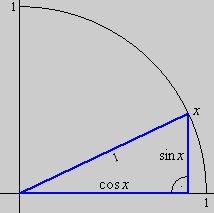
Die trigonometrischen Funktionen spielen nicht nur in der Mathematik selbst, sondern auch in ihren Anwendungsgebieten, speziell in der Physik, eine bedeutende Rolle. Ihre Ursprünge reichen sehr weit zurück und im Gegensatz zu den bisherigen Funktionen liegen ihre Wurzeln deutlich im geometrischen Bereich, und zwar in der Dreieckslehre. Unsere Einführung der trigonometrischen Funktionen trägt zunächst dieser geometrischen Herkunft Rechnung.
Die in der Dreieckslehre übliche Methode, Winkel in Graden zu messen, ist allerdings für unsere Zwecke ungeeignet. Ein geeignetes Maß, Winkel in Zahlen und nicht in Graden zu messen, ist das Bogenmaß (engl. radian). Die Grundidee liegt dabei in der Beobachtung, dass jeder Winkel, im Mittelpunkt eines vorgelegten Kreises angetragen, einen Ausschnitt des Kreisesbogens liefert. Da allerdings ein Winkel bei verschieden großen Kreisen unterschiedliche große Bögen ausschneidet, ist eine Festlegung auf einen bestimmten Kreis zwingend. Zur Winkelmessung durch Bögen werden wir daher stets einen Kreis mit Radius 1 und Mittelpunkt im Ursprung des Koordinatensystems zu Grunde legen, den sog. Einheitskreis.
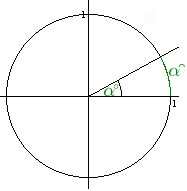 Jedem gemäß nebenstehender Skizze eingetragenem Winkel kommt nun neben seinem (orientierten) Gradmaß auch sein (orientiertes) Bogenmaß (auch: α rad), d.h. die Länge des von ihm ausgeschnittenen Bogens zu. Dabei bezieht sich der Zusatz "orientiert" auf die Vereinbarung, dass im Gegenuhrzeigersinn (wie in der Skizze) eingezeichnete Winkel positive Maßzahlen haben, und Winkeln, die im Uhrzeigersinn eingetragen sind, negative Maßzahlen zukommen. Jedem gemäß nebenstehender Skizze eingetragenem Winkel kommt nun neben seinem (orientierten) Gradmaß auch sein (orientiertes) Bogenmaß (auch: α rad), d.h. die Länge des von ihm ausgeschnittenen Bogens zu. Dabei bezieht sich der Zusatz "orientiert" auf die Vereinbarung, dass im Gegenuhrzeigersinn (wie in der Skizze) eingezeichnete Winkel positive Maßzahlen haben, und Winkeln, die im Uhrzeigersinn eingetragen sind, negative Maßzahlen zukommen.
Natürlich kann man die beiden Maßsysteme ineinander umrechnen. So liefert z.B. ein Winkel vom Gradmaß den halben Umfang des Einheitskreises, also die Zahl als Bogenmaß. Daraus ergibt sich für einen beliebigen Winkel :
Ist das Gradmaß von , so ist das Bogenmaß von . |
Ist das Bogenmaß von , so ist das Gradmaß von . |
Grad- und Bogenmaße einiger markanter Winkel kann man direkt aus der folgenden Tabelle ablesen. Für beliebige Winkel leistet das nachstehende Umrechnungsformular gute Dienste. Es berücksichtigt bis zu 8 Dezimalstellen.
Nun können wir die beiden ersten trigonometrischen Funktionen, nämlich die Sinus- und die Cosinusfunktion
einführen. Statt einer präzisen Funktionsvorschrift geben wir hier eine geometrisch ausgerichtete Konstruktionsvorschrift an und tragen die exakte Definition in einem
späteren Abschnitt
i   |
|
In [5.9] setzen wir , bzw. als Grenzwert einer konvergenten Potenzreihe fest, und zwar
Da diese Definition auch im Komplexen möglich ist, liegen Sinus und Cosinus auch als Funktionen von vor. Darüber hinaus sind wir erst mit dieser analytischen Definition in der Lage, exakte Beweise zu führen.
|
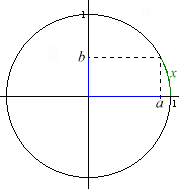
nach. Eine gegebene reelle Zahl interpretieren wir als das Bogenmaß eines Winkels und tragen dieses Maß am Einheitskreis ab (positive Zahlen im Gegenuhrzeigersinn, negative im Uhrzeigersinn). Dadurch legen wir eindeutig einen von x abhängigen Punkt auf dem Kreis fest. Seine beiden Koordinaten a und b sind nun die Funktionswerte.
|
Definition: Für setzen wir gemäß der vorgestellten Konstruktion fest:
 |
|
[4.3.1] |
Es ist üblich, die Funktionswerte klammerfrei zu schreiben, also: bzw. .
|
Im allgemeinen wird man mit dieser Methode keine exakten Funktionswerte ermitteln können, für einige speziell gewählte x-Werte lassen sich und jedoch leicht am Einheitskreis ablesen:
Wir erläutern das Ablesen an zwei Beispielen:
-
Der zu gehörige Bogen ist ein Viertelkreis, der bei startet und bei endet. Die Koordinaten des Endpunkts sind die sin- bzw. cos-Werte: 1 ist der Sinuswert und 0 der Cosinuswert.
-
Zu gehört ein Bogen der Länge 0. Er endet also bereits im Startpunkt , d.h. der Sinuswert ist hier 0 und der Cosinuswert 1.
Um einen Funktionsgraphen zu zeichnen, reichen diese Daten allein natürlich nicht aus. Das folgende Applet simuliert jedoch die geometrische Konstruktion für die Sinusfunktion und stellt ausreichend viele Werte zur Verfügung. Mit dem Schieber kann man den Graphen bequem erzeugen.
sin und cos besitzen eine Fülle von Eigenschaften. Viele ergeben sich zwar direkt aus der Konstruktion über den Einheitskreis, ihre Gültigkeit aber können wir damit nicht sicherstellen. Für die weiteren Ausführungen legen wir daher die Definition aus [5.9] zu Grunde, also:
[0]
Da durch [0] auch die komplexen Funktionen sin und cos definiert sind, hat dies zudem den Vorteil, dass (fast) jede der hier notierten Aussagen automatisch auch im Komplexen gültig ist.
Allerdings müssen wir erst sicherstellen, dass die durch [0] definierten Funktionen mit den geometrisch eingeführten identisch sind! Wir zeigen dies mit Techniken der Integralrechnung auf einer eigenen Seite. Ferner benötigen wir genauere Informationen über die Zahl . Dazu vergewissern wir uns zunächst, dass die Sinusfunktion positive Nullstellen besitzt.
|
Bemerkung: Es gibt eine reelle Zahl , so dass
|
[4.3.2] |
Beweis: Wir benötigen einige Abschätzungen. Zunächst hat man für und :
Für diese x gilt daher:
,
und damit schließlich:
für alle . [+]
Somit ist z.B. und mit einer weiteren Abschätzung finden wir:
Da sin stetig ist ([6.2.17]), gibt es gemäß Nullstellensatz [6.6.1] eine Nullstelle zwischen 2 und 4.
|
In gilt das Vollständigkeitsaxiom, d.h. jede nicht-leere, nach unten beschränkte Teilmenge besitzt eine größte untere Schranke, das Infimum. Mit [4.3.2] können wir daher festsetzen:
|
[4.3.3] |
Dabei garantieren [+] und die letzte Abschätzung dass . Insbesondere ist damit .
Von entscheidender Bedeutung für die Eigenschaften der trigonometrischen Funktionen sind die sog. Additionstheoreme.
|
Satz (Additionstheoreme): Für alle ist
-
-
|
[4.3.4] |
Beweis: Mit den Abkürzungen
und
können wir [0] umschreiben zu
[1]
Wir beweisen jetzt das Additionstheorem für den Sinus. Der Nachweis für den Cosinus verläuft ähnlich und kann hier aufgerufen werden.
Wir berechnen nun zunächst für :
Man beachte dabei: .
Mit Hilfe des Binomialtheorems [5.2.5] und der Produktregel für konvergente Reihen

i   |
|
haben wir jetzt:
Wir berechnen nun zunächst für :
Man beachte dabei: .
Mit Hilfe des Binomialtheorems [5.2.5] und der Produktregel für konvergente Reihen

i   |
|
haben wir jetzt:
|
Wir stellen nun weitere Eigenschaften der trigonometrischen Funktionen zusammen und beginnen mit einer Information zur Symmetrie: sin ist punkt- und cos achsensymmetrisch.
|
Bemerkung: Für alle ist
-
-
|
[4.3.5] |
Beweis:
1. ► .
2. ► .
|
Nun gelingt es auch, einige der anschaulich gewonnenen Funktionswerte rechnerisch zu bestätigen.
|
Bemerkung:
|
[4.3.6] |
Beweis:
-
Da ist gleich 0 für und gleich 1 für hat man sofort:
und .
-
: Gemäß [4.3.3] kann es unterhalb von keine positiven Nullstellen des Sinus geben, also ist für alle . Ist nun , so gilt dies aus Stetigkeitsgründen in ganzen Umgebung von . Es gibt also ein , o.E. , so dass in . Damit aber hat man
für alle
und folglich: - Widerspruch.
-
: Mit dem Additionstheorem für den Sinus erhält man
.
Man beachte, dass , da (siehe [4.3.3]). Also ist .
-
: Diesmal setzen wir das Additionstheorem für den Cosinus ein und erhalten unter Beachtung der Symmetrie [4.3.5]:
,
also . Das aber ist nach [+] die Behauptung, denn da , ist .
-
: Wir greifen auf die beiden letzten Ergebnisse und das Additionstheorem zurück:
.
-
: .
-
: .
-
: .
-
: .
|
Da nun einige markante Funktionswerte sicher sind, lassen sich weitere Eigenschaften nachweisen. Wir haben u.a. eine zusätzliche Notiz zur Symmetrie, zur Periodizität und zum Nullstellenverhalten.
|
Bemerkung: Für alle gilt:
-
|
[4.3.7] |
|
sin und cos lassen sich durch waagerechtes Verschieben in die jeweils andere Funktion überführen: Verschiebt man sin um Einheiten erhält man den Cosinus, Verschiebt man cos um Einheiten erhält man den Sinus. In 4.6 wird diese Technik näher beschrieben.
|
-
|
[4.3.8] |
|
Der Sinus ist symmetrisch zur Senkrechten und der Cosinus punktsymmetrisch zu .
|
-
für jedes
für jedes
|
[4.3.9] |
|
sin und cos wiederholen ihre Werte im Abstand von , sie sind also -periodisch.
|
-
für ein
für ein
|
[4.3.10] |
|
Die Nullstellen des (reellen) Sinus sind genau die geraden Vielfachen von , die des Cosinus genau die ungeraden. Im Komplexen gibt es keine weiteren Nullstellen.
|
-
|
[4.3.11] |
|
Diese Gleichheit, oft abgekürzt zu , ist der Satz des Pythagoras, denn und sind die Kathetenlängen eines rechtwinkligen Dreiecks dessen Hypotenuse die Länge 1 hat.

i   |
|
|
|
-
|
[4.3.12] |
|
Diese Abschätzungen belegen die Beschränktheit von sin und cos, eine Eigenschaft die nur im Reellen gültig ist!
|
Beweis: Wir benötigen lediglich die Additionstheoreme und das Symmetrieverhalten.
1. ► .
.
2. ► .
.
3. ► Wir zeigen zunächst per Induktion:
für alle .
Für ist nichts zu zeigen, der Induktionsanfang also trivial. Ist nun die Aussage für ein bereits gültig, so hat man:
Damit ist 3. für den Sinus bewiesen. Weiterhin haben wir damit für ein beliebiges :
.
4. ► Wir betrachten zunächst nur den Sinus und haben hier wegen der Periodizität:
sin ist also sowohl an den geraden wie auch an den ungeraden Vielfachen von π gleich Null, d.h. jedes Vielfache von π ist eine Nullstelle.
Sei jetzt x eine beliebige Nullstelle des Sinus. Wir müssen zeigen, dass x ein Vielfaches von π ist. O.E. sei dabei , denn für ist nichts zu zeigen und nach [4.3.5] ist mit x auch eine Nullstelle.
Mit grenzen wir zunächst die Lage von x ein: . Für
ist dann , ja sogar , denn wegen der Periodizität ist und gemäß [4.3.3] liegen unterhalb von π keine positiven Nullstellen. Ist nun , also
,
so ist nichts weiter zu zeigen. Ist dagegen , so hat man , und da
,
muss , also , gelten (wieder mit [4.3.3]) und damit:
.
Die Nullstellen des Cosinus sind jetzt mit [4.3.7] leicht zu beschreiben:
5. ► Mit dem Additionstheorem [4.3.4] für den Cosinus und dem Symmetrieverhalten hat man:
.
6. ► Da (in ) Quadrate stets positiv sind, hat man nach 5. z.B. für den Sinus:
,
also: . Das ist die Behauptung.
|
Mit einem kleinen Exkurs in die Physik, und zwar in die Schwingungslehre, stellen wir Modifikationen der Sinusfunktion vor. Dort beschreibt eine Funktion des Typs
eine ungedämpfte Schwingung, wie sie etwa bei einer idealen Pendelbewegung auftritt. Die x-Achse wird hier als "Zeitachse" interpretiert, so dass π als Einheit ungünstig ist; statt dessen kehren wir wieder zu 1 als Einheit zurück und messen mit ihr z.B. Sekunden. Auch die Namen der Parameter haben hier ihren Ursprung:
-
Die Amplitude | a | gibt die maximale Auslenkung (Elongation) der Schwingung an.
-
Mit der Kreisfrequenz ω berechnet man die Frequenz ν der Schwingung: ist die Anzahl der Perioden pro Zeiteinheit. Die Schwingungsdauer gibt die für eine Periode benötigte Zeit an.
-
Allgemein nennt man den Phasenwinkel und speziell φ den Nullphasenwinkel, bzw. die Phasenverschiebung der Schwingung. Sie bestimmt die Anfangselongation .
Unter den Schwingungen kommen Sinus () und Cosinus () natürlich auch vor. Man beachte, dass die Pixelgrafik bei hohen Frequenzen überfordert ist. Die Darstellung entspricht dann nicht mehr der angegebenen Funktion, zeigt aber z.T. eine interessante Periodiztät. Ich habe daher in diesen Fällen auf ein Ausblenden verzichtet.

i   |
|
|
Amplitude
1
|
Frequenz
0.1591545
|
Schwingungs-
dauer
6.2831853
|
Anfangs-
elongation
0
|
|
|
Mit Hilfe von Sinus und Cosinus führen wir nun zwei weitere trigonometrische Funktionen ein. Allerdings werden bei den Funktionsvorschriften Divisionen durchgeführt, so dass die Definitionsbereiche geeignet zu wählen sind. [4.3.10] gibt uns dabei Auskunft über die Lage der Nullstellen von sin und cos.
|
Definition: Die Funktionen
gegeben durch
|
[4.3.13] |
gegeben durch
|
[4.3.14] |
sind der Tangens und der Cotangens.
Auch hier werden die Funktionswerte meist klammerfrei geschrieben: bzw. . Man beachte ferner, dass beide Funktionen unendliche viele Definitionslücken besitzen, und zwar Polstellen. Dabei sind die Polstellen des Tangens genau die Nullstellen des Cosinus und die des Cotangens genau die Nullstellen des Sinus.
|
Die Werte sind direkt einsehbar. Mit ein wenig Mühe finden wir auch einen nicht trivialen Wert: Mit dem Additionstheorem hat man zunächst
,
und daraus mit Pythagoras:
.
Also sind und identisch.

i   |
|
und zwar ist
,
denn wieder mit Pythagoras ist
Also ist , denn nach [+] ist .
|
Das aber bedeutet:
.
Wir stellen den Tangens in einer Skizze vor. Dabei verzichten wir auf Bezüge zur Physik und betrachten jetzt Funktionen der Form

i   |
|
|
|
|
Tangens und Cotangens besitzen zahlreiche Eigenschaften. Naturgemäß sind sie in der Regel direkt auf entsprechende Sachverhalte bei sin und cos zurückzuführen. Die folgende Bemerkung stellt einige Eigenschaften zusammen.
|
Bemerkung: Für alle mit bzw. gilt:
-
|
[4.3.15] |
|
Die beiden Funktionen gehen durch waagerechtes Verschieben um und anschließendes Spiegeln an der x-Achse ineinander über.
|
-
für ein
für ein
|
[4.3.16] |
|
Der Tangens hat also dieselben Nullstellen wie sin, der Cotangens dieselben wie cos.
|
-
|
[4.3.17] |
|
Sind beide Funktionswerte gleichzeitig vorhanden, so ist der eine stets Kehrwert des anderen.
|
-
|
[4.3.18] |
|
Tangens und Cotangens sind punktsymmetrisch.
|
-
für jedes
für jedes
|
[4.3.19] |
|
Tangens und Cotangens sind π-periodisch.
|
|
[4.3.20] |
|
|
für
für
|
[4.3.21] |
|
Das sind die Additionstheoreme für Tangens und Cotangens.
|
Beweis:
1. ► Mit [4.3.8] und [4.3.7] ergibt sich:
,
und damit:
.
2. ► wird genau dann Null, wenn der Zähler gleich Null ist. Nach [4.3.10] also genau dann, wenn ist. Beim Cotangens argumentiert man analog.
3. ► .
4. ► Wir benutzen das Symmetrieverhalten [4.3.5]:
.
Die entsprechende Eigenschaft des Cotangens erhält man analog.
5. ► Wir benötigen einige Vorüberlegungen. Zunächst erhält man mit [4.3.8]:
und über die Periodizität von Sinus und Cosinus dann auch:
Damit schließlich haben wir:
. [++]
Nun zeigen wir per Induktion: für alle . Da für offensichtlich nichts zu tun ist, bleibt nur der Induktionsschluss: Mit [++] ergibt sich aus der Induktionsvoraussetzung:
.
Nun zum Cotangens: Ist x, und damit auch , ein ungerades Vielfaches von , so hat man nach [4.3.16]: . In allen anderen Fällen greift man auf das gerade Bewiesene zurück:
.
6. ► Diese Gleichungen ergeben sich aus dem Satz des Pythagoras [4.3.11], z.B. für den Tangens:
.
7. ► Mit den Additionstheoremen [4.3.4] für Sinus und Cosinus beweisen wir die erste Gleichung:
Falls (), gelingt damit auch der Nachweis der zweiten Gleichung:
.
Ist , so steht auf beiden Seiten der Gleichung Null.
|
|
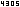 |
|
 Jedem gemäß nebenstehender Skizze eingetragenem Winkel kommt nun neben seinem (orientierten) Gradmaß auch sein (orientiertes) Bogenmaß (auch: α rad), d.h. die Länge des von ihm ausgeschnittenen Bogens zu. Dabei bezieht sich der Zusatz "orientiert" auf die Vereinbarung, dass im Gegenuhrzeigersinn (wie in der Skizze) eingezeichnete Winkel positive Maßzahlen haben, und Winkeln, die im Uhrzeigersinn eingetragen sind, negative Maßzahlen zukommen.
Jedem gemäß nebenstehender Skizze eingetragenem Winkel kommt nun neben seinem (orientierten) Gradmaß auch sein (orientiertes) Bogenmaß (auch: α rad), d.h. die Länge des von ihm ausgeschnittenen Bogens zu. Dabei bezieht sich der Zusatz "orientiert" auf die Vereinbarung, dass im Gegenuhrzeigersinn (wie in der Skizze) eingezeichnete Winkel positive Maßzahlen haben, und Winkeln, die im Uhrzeigersinn eingetragen sind, negative Maßzahlen zukommen.