4.2. Beispiele
In diesem Abschnitt stellen wir einige Standardfunktionen vor. Obwohl die meisten von
ihnen auch im Komplexen vorliegen, beschränken wir uns hier auf den reellen Fall und haben so die Möglichkeit, Skizzen anzufertigen, ein nicht zu unterschätzender Lernvorteil.
Die hier besprochenen Funktionen benutzen wir häufig, so dass es sich für sie lohnt, den allgemeinen Namen f durch einen individuellen zu ersetzen. Bei den in 4.3 zu betrachtenden trigonometrischen Funktionen etwa sind die Namen sin und cos gebräuchlich. Oft ist die Funktionsvorschrift einer Funktion so aussagekräftig, dass es sich anbietet, sie als Namen zu verwenden. Ist z.B. die Funktion
durch gegeben,
so könnte man x als Namen für f verwenden. Diese Idee scheitert jedoch, da zwischen der Funktion f und einem ihrer Werte zu unterscheiden ist. Wir umgehen dieses kleine philosophische Problem durch einen schreibtechnischen Trick und ersetzen x durch X. Wir bezeichnen also im Folgenden die hier vorliegende Funktion f mit dem Symbol X. f trägt somit einen Namen, der ihre Arbeitsweise bereits sichtbar macht.
Die folgenden Beispiele verdeutlichen diese Technik der Namensgebung. Die jeweils aufrufbaren Graphen sind manipulierbar. Über die Einstellmöglichkeiten informiert diese Skizze.
|
Beispiel:
Lineare Funktionen |
Potenz-
funktionen |
Kehrwert-
funktion |
Wurzel-
funktion |
Betrags-
funktion |
Heaviside-
Funktion |
ceiling
floor
round |
-
Für heißt die Funktion linear, falls
,
|
[4.2.1] |
d.h. also falls . Die Graphen der linearen Funktionen sind stets Geraden. Über ihre Lage im Koordinatensystem geben die Parameter b und m Auskunft:
Da , also , gibt b den Schnittpunkt mit der y-Achse an.
Die Steigungszahl m ist ein Maß für die Steigung der Geraden in folgendem Sinn: Sind und zwei verschiedene Geradenpunkte, so ist m der (immer gleiche) Wert des Quotienten
,
denn: .
Ferner steuert das Vorzeichen von m die Richtung der Geraden: f ist steigend, falls m positiv und fallend, falls m negativ ist.
Außerdem hat man offenbar: Zwei Geraden sind genau dann parallel wenn sie denselben Steigungsfaktor besitzen.
-
Die Nullstellen von f sind die Lösungen der Gleichung . Für
hat f daher genau eine Nullstelle, und zwar in .
Da eine Gerade bereits durch zwei Punkte festgelegt ist, lassen sich lineare Funktionen sehr leicht skizzieren. Das Markieren zweier Punkte gelingt mit den Parametern b und m sehr schnell. Wir zeigen dies, mit Hilfe des blauen Schiebers, am Beispiel der Funktion
:
Zwei Spezialfälle zeichnen wir durch einen eigenen Namen aus:
-
Für und erhalten wir die bereits im Eingangstext erwähnte Funktion . Wir nennen sie die Identität (oder auch die identische Funktion) auf . Man hat also (und das erläutert auch den Namen):
.
|
[4.2.2] |
Wir verwenden gelegentlich das Symbol , falls es nötig ist, die identische Funktion von anderen Identitäten zu unterscheiden.
Ihr Graph ist die erste Winkelhalbierende, denn der Steigungszahl entspricht ein Winkel von 45° und mit liegt zudem eine Ursprungsgerade vor.
-
Ist , so nennen wir die Funktion b (oder auch ) die konstante Funktion b auf . Hier gilt:
.
|
[4.2.3] |
Da , ist der Graph von b eine Waagerechte, die die y-Achse in b schneidet.
Im folgenden Applet stellen wir lineare Funktionen graphisch dar. Wir beginnen mit der Identität X:

i   |
|
|
Nullstelle:
0
|
|
|
-
Zunächst betrachten wir die Quadratfunktion gegeben durch
.
|
[4.2.4] |
Ihr Graph ist die nach oben geöffnete Normalparabel. Da , geht sie durch den Koordinatenursprung . Wegen ist dies sogar der tiefste Punkt der Parabel und die durch ihn gehende y-Achse ist ihre Symmetrieachse:
.
Wir nennen den Scheitelpunkt, oder kurz den Scheitel von .
Mit der Identität X haben wir die Gruppe der linearen Funktionen erzeugt. Analog gewinnen wir aus der Quadratfunktion die allgemeinen quadratischen Funktionen, also Funktionen des Typs
.
|
[4.2.5] |
O. E. sei dabei , denn sonst wäre f linear. Die Bedeutung der Parameter erschließt sich hier nicht sofort. Zwar hat man , d.h. die Funktion schneidet die y-Achse bei c, um aber a und b besser einordnen zu können, werden wir zunächst den Funktionsterm mit Hilfe der quadratischen Ergänzung umformen:
Mit den Abkürzungen und ist also:
.
Diese Darstellung nennen wir die Scheitelpunktform von f und den Scheitel von f. Wir haben denn auch:
-
gehört zu f, denn .
-
ist tiefster/höchster Punkt von f, denn ist stets positiv, falls und stets negativ, falls .
-
Die durch u gehende Senkrechte ist Symmetrieachse von f:
.
Der Graph einer beliebigen quadratischen Funktion ist also wieder eine Parabel. b bestimmt dabei (in Kombination mit a) den x-Wert des Scheitels und, bis auf den Summanden c, auch seinen y-Wert.
a gibt über sein Vorzeichen die Öffnungsrichtung der Parabel an. a selbst ist der konstante Wert
denn für hat man: , also: . Das aber bedeutet: Entfernt man sich in der Waagerechten um k Einheiten vom Scheitel, so trifft man nach Einheiten in der Senkrechten wieder auf den Graphen.
Die folgenden Skizzen berechnen sowohl die Scheitelpunktform wie auch die Nullstellen von f, also die Lösungen der quadratischen Gleichung .

i   |
|
|
Nullstellen:
0
|
|
|
-
Man wird dieses Spiel fortsetzen: Die Kubikfunktion etwa erzeugt die allgemeinen kubischen Funktionen , usw. Wir widmen diesem Prinzip ein eigenes Kapitel (4.5) und begnügen uns hier mit einigen Skizzen kubischer Funktionen, den sog. kubischen Parabeln,

i   |
|
|
Nullstellen:
0
|
|
|
-
und wenden uns den eigentlichen Erzeugerfunktionen zu: Für heißt die Funktion gegeben durch
|
[4.2.6] |
die Potenzfunktion zum Exponenten n.
Die Potenzfunktion zum Exponenten 0 ist die konstante Funktion 1. Alle anderen gehen durch die Punkte und . Ist
-
n gerade, so geht auch durch und ist zudem achsensymmetrisch: .
-
n ungerade, so geht auch durch und ist punktsymmetrisch: .
Die Graphen der Potenzfunktionen sind recht überschaubar. Ihre Gestalt ähnelt den Graphen der gewöhnlichen, bzw. kubischen Parabel.
i   |
|
|
-
Die Funktion
gegeben durch
|
[4.2.7] |
heißt die Kehrwertfunktion. Sie hat keine Nullstellen, denn der Zähler wird nie 0, aber einen eingeschränkten Definitionsbereich, da 0 keinen Kehrwert besitzt. Daher besteht ihr Graph, die Hyperbel, aus zwei getrennten Ästen. Allgemeinere Hyperbeln erhält man durch Funktionen der Form
Auch diese Funktionen haben einen eingeschränkten Definitionsbereich, da der Nenner Nullstellen besitzt. Sie heißen Polstellen von f und werden in den folgenden Skizzen mit angegeben. Für gibt es hier nur eine Polstelle, nämlich . Ist , so ist f die leere Funktion!

i   |
|
|
Polstelle:
0
|
|
|
-
Wir können die Kehrwertfunktion als eine Potenzfunktion auffassen, denn für nennen wir die Funktion gegeben durch
|
[4.2.8] |
die Potenzfunktion zum Exponenten . Alle Potenzfunktionen mit einem negativen Exponenten besitzen in 0 eine Polstelle und gehen durch den Punkt , bei geradem n auch durch und bei ungeradem durch . Ihre Graphen wechseln ebenfalls nur zwischen zwei Grundformen, dabei ist achsensymmetrisch falls n gerade und punktsymmetrisch falls n ungerade ist.

i   |
|
|
-
Die Funktion gegeben durch
|
[4.2.9] |
heißt die Wurzelfunktion. Gelegentlich wird das Symbol durch ersetzt.
Da im Reellen nur die positiven Zahlen Wurzeln besitzen, hat die Wurzelfunktion naturgemäß den Definitionsbereich . Außerdem sind alle Wurzelwerte positiv, so dass für die Skizze der erste Quadrant ausreicht.
Von ihren Variationsmöglichkeiten sollen hier beispielhaft diejenigen betrachtet werden, die durch die Form
gegeben sind.

i   |
|
|
Nullstelle:
0
|
Definitions-
bereich: [0,∞[
|
|
|
Eine besondere Bedeutung kommt der Wurzelfunktion bei der Erzeugung von Kreisen und Ellipsen zu. Wir zeigen dies beispielhaft für einen Kreis mit Radius :
Gemäß Pythagoras stellt die Menge einen Kreis mit Radius r und Mittelpunkt dar. Allerdings kann dieser Kreis nie Graph einer Funktion sein, da hier den x-Werten zwei y-Werte zukommen. Der obere Halbkreis dagegen könnte dies sehr wohl, falls f eine Funktion auf ist, deren Werte positiv sind und die Gleichung
erfüllen. f muss daher durch die Funktionsvorschrift
gegeben sein. Einen (oberen) Halbkreis mit beliebigem Mittelpunkt gewinnen wir nach einer kleinen Manipulation durch die Funktion
.
Schließlich erzeugt für die Funktion
eine Halbellipse mit den Halbachsen a und b und Mittelpunkt . Der Sonderfall führt dabei wieder auf einen Kreis zurück.

i   |
|
|
|
|
-
Die Funktion gegeben durch
|
[4.2.10] |
heißt die Betragsfunktion. Alternativ kann man auch das Symbol verwenden.
Ihre Funktionswerte sind Beträge reeller Zahlen, also grundsätzlich positiv. Daher liegt der Graph der Betragsfunktion oberhalb der x-Achse. Die rechts stehende Variante der Funktionsvorschrift zeigt, dass der Graph im Positiven mit der 1. und im Negativen mit der 2. Winkelhalbierenden zusammenfällt. Man beachte den Knick im Koordinatenursprung.
Wir variieren die Betragsfunktion hier durch Funktionen der Form
.

i   |
|
|
Nullstellen:
0
|
|
|
Die Funktionsvorschrift der Betragsfunktion stellt eine bestimmte Technik vor, nämlich die, eine Funktion abschnittsweise zu definieren. Damit ist das folgende Prinzip gemeint: Ist eine (disjunkte) Zerlegung der Menge A und sind bereits gegebene Funktionen, so wird durch die Festsetzung
|
[4.2.11] |
eine Funktion definiert.
-
Die Funktion gegeben durch
|
[4.2.13] |
ist die Heaviside-Funktion. Gebräulich ist auch der Name Theta-Funktion mit dem Symbol .
Obwohl die Heaviside-Funktion auf ganz erklärt ist, besteht ihr Graph aus zwei getrennten Anteilen! Man sagt gelegentlich, H macht bei 0 einen Sprung und nennt die Heaviside-Funktion deshalb auch eine Treppenfunktion. Interessanterweise lassen sich allein aus ihr alle weiteren Treppenfunktionen konstruieren. Einige Beispiele dazu kann man bereits durch Funktionen des Typs
selbst erzeugen.

i   |
|
|
Sprungstelle:
0
|
|
|
Schließlich beachte man: H ist keine konstante Funktion, denn der Wertebereich von H enthält zwei Elemente.
Die Heaviside-Funktion ist ein spezielles Beispiel einer zu einer Menge gehörenden Indikatorfunktion oder, wie man auch sagt, charakteristischen Funktion. Indikatorfunktionen nehmen nur die Werte 0 und 1 an, und zwar den Wert 1 genau dann, wenn ein Element x der vorgelegten Menge ansteht. Für eine Teilmenge definieren wir also:
Die Funktion gegeben duch
|
[4.2.14] |
heißt charakteristische Funktion (oder Indikatorfunktion) zu A. Verwendet man den Begriff Indikatorfunktion, so ist das Symbol gebräuchlicher.
So ist z.B. die Heavisidefunktion eine Indikatorfunktion, nämlich die zu : . Aber auch die konstanten Funktionen 0 und 1 lassen sich als Indikatorfunktionen darstellen:
.
Eine sehr interessante Indikatorfunktion ist , die charkteristische Funktion zur Menge der rationalen Zahlen . Obwohl ihr Graph eine Teilmenge von ist, gelingt eine graphische Darstellung nicht! Denn an jeder rationalen Stelle x muss ein Punkt in Höhe 1 gezeichnet werden; da aber die rationalen Zahlen dicht in liegen, entsteht eine Waagerechte, die sich optisch nicht von der Konstanten 1 unterscheidet. Genauso aber muß für jede irrationale Zahl ein Punkt in Höhe 0 gezeichnet werden. Auch hier entsteht wegen der Dichtheit der irrationalen Zahlen eine Waagerechte, die sich nicht sichtbar von der x-Achse unterscheidet, so dass der Graph von bestenfalls aus zwei parallelen Geraden besteht. Damit aber täuscht er eine Doppeldeutigkeit der Funktionswerte vor, die keine Funktion zulässt.
Die Funktionen dieser Gruppe treten oft bei Programmieraufgaben auf (ihre Namen stammen direkt aus der Sprache Java!), wenn es z.B. darum geht, einer Gleitkommazahl (d.h. einer Dezimalzahl) einen geeigneten Integer-Wert (eine ganze Zahl) zuzuordnen. Hier werden drei Varianten vorgestellt:
-
Das Abschneiden der Nachkommastellen, "auf den Boden setzen".
-
Das Auffüllen zur nächsten ganzen Zahl, "an die Decke hängen".
-
Das übliche Runden.
Wir führen alle drei Funktionen gemeinsam ein.
-
Die Funktionen gegeben durch
|
[4.2.15] |
heißen die ceiling-Funktion, die floor-Funktion und die round-Funktion. So ist z.B.
| x |
|
|
|
|
|
4 |
3 |
4 |
3.53 |
Alle drei Funktionen haben per Definition nur ganzzahlige Funktionswerte, ihr Wertebereich ist also eine Teilmenge von und, da für jedes n, sogar gleich .
-
Mit Hilfe der round-Funktion kann man auch das "Runden auf n Stellen nach dem Komma" einführen. Dazu setzen wir für
.
-
floor ist ein neuerer Name für die altbekannte Gauß-Funktion. Verwendet man diesen Namen, so benutzt man die Gaußklammer als Funktionssymbol. ist also eine alternative Schreibweise zu :
.
Der Graph von ist ebenfalls eine Treppenfunktion, jedoch eine mit unendlich vielen Stufen! Dabei lassen sich z.B. Schrittweite und Stufenhöhe noch variieren, wenn man Funktionen der Form
betrachtet.

i   |
|
|
|
|
Lineare Funktionen |
Potenz-
funktionen |
Kehrwert-
funktion |
Wurzel-
funktion |
Betrags-
funktion |
Heaviside-
Funktion |
ceiling
floor
round |
|
|
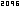 |
|