4.1. Einführung
Der Funktionsbegriff ermöglicht es, zwischen zwei Mengen, genauer zwischen ihren Elementen, Beziehungen aufzustellen und diese zu studieren.
Die beiden Mengen sollen dabei eine unterschiedliche Rolle spielen: Wir werden die Elemente einer (links notierten) Menge A als Ausgangsobjekte ansehen, denen die Elemente einer Menge B als Zielobjekte zugewiesen werden. Diese Vorstellung spiegelt sich im folgenden anschaulichen Bild wider: der von x ausgehende Pfeil drückt aus, dass diesem Element das Element zur Seite gestellt wird.
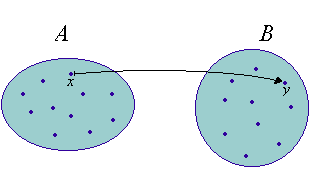 Dieses Zuweisungskonzept soll durch einige Bedingungen strukturiert werden: Zum einen sollen die Elemente der linken Menge allesamt mit Bildelementen aus der rechten Menge versorgt werden, d.h. in der obigen Darstellung müsste von jedem Punkt in A ein Pfeil starten. Zum anderen soll jedes x sein individuelles Bild erhalten, d.h. von jedem Element aus A darf auch nur ein Pfeil starten (was im übrigen nicht ausschließt, dass auf ein y mehrere Pfeile zielen, oder auch gar keine).
Der zentrale Gedanke unseres Funktionsbegriffs ist es also, Elementen x jeweils ein weiteres Element y zur Seite zustellen; in Sprache der Mengenlehre heißt dies: Paare bilden. Man kann somit eine Funktion auffassen als die Gesamtheit aller zu ihr gehörenden Paare und nun exakt definieren:
|
Definition: A und B seien irgendzwei Mengen. Eine Menge ist eine Funktion von A nach B, falls es
zu jedem genau ein gibt, so dass ist.
|
[4.1.1] |
|
Um zu entscheiden, ob eine Teilmenge f von eine Funktion ist, müssen also zwei Punkte geprüft werden:
Kommt jedes als linke Koordinate eines Paares aus f vor? Ist f also linkstotal? Gibt es zu jedem x genau ein , so dass das Paar zu f gehört?
D.h. ist f rechtseindeutig?
Für die mit einer Funktion gegebenen Daten führen wir eigene Begriffe ein:
A ist der Definitionsbereich und B der Bildbereich von f. Die Menge ist der Wertebereich von f.
Ist , so nennen wir y das Bild von x (bzgl. f) oder auch den Funktionswert von f an der Stelle x, falls . In diesem Fall ersetzen wir das Element y durch das Symbol , d.h. wir notieren die Information als .
Ist , so nennen wir x ein Urbild von y oder auch eine y-Stelle (bzgl. f), falls .
Beachte:
Jedem darf nur ein zugewiesen sein! Erst dies erlaubt es, den Ausdruck durch zu ersetzen und das Bild von x zu nennen. Eine analoge Forderung an y gibt es nicht; es ist also durchaus möglich, dass ein y das Bild mehrerer x ist. Die Formulierung ein Urbild trägt dieser Situation Rechnung. Es kann auch vorkommen, dass ein y überhaupt kein Urbild besitzt. Mit Hilfe des Symbols lässt sich der Wertebereich einer Funktion übersichtlicher beschreiben. Auch kommt jetzt deutlicher zum Ausdruck, dass es sich dabei um die Menge der tatsächlich angenommen Funktionswerte handelt:
Zwischen einer Funktion und einem ihrer Werte ist strikt zu trennen. Schließlich ist f eine Teilmenge von und "nur" ein einfaches Element von B. f und bezeichnen also sehr verschiedene Objekte! Zwei Funktionen sind genau dann gleich (in Zeichen: ) wenn sie dieselbe Teilmenge von darstellen, wenn also für jedes die Gleichheit gegeben ist. Es gibt genau eine Funktion von , nämlich , die leere Funktion.
Beweis:
Da , ist die leere Menge die einzige Teilmenge von ; sie ist auch eine Funktion, denn jede Forderung an ein ist automatisch erfüllt, weil ein solches x gar nicht existiert. Begründet ist dies in der Logik: Eine Aussage der Form ist immer wahr, sobald a falsch ist!
Ist , so gibt es keine Funktion von .
Beweis:
Auch hier ist die leere Menge die einzige Teilmenge von , so dass höchstens die leere Funktion als Funktion von infrage kommt. Da es aber mindestens ein gibt, müßte es auch ein geben, so dass . Ein solches y aber kann es nicht geben.
|
Beispiel:
-
ist eine Funktion von nach , denn jedes der drei Elemente von bildet mit genau einem Element von ein Paar.
Offensichtlich hat das Element 3 zwei Urbilder, nämlich a und c. 1, 2 und 4 haben dagegen überhaupt keine Urbilder, in diesem Fall sind also Werte- und Bildbereich nicht identisch. Der Wertebereich ist "nur" die Menge .
-
ist keine Funktion von nach , denn dem Element a sollen hier zwei Bilder zugewiesen werden, nämlich 1 und 2.
-
ist ebenfalls keine Funktion von nach , denn es fehlt ein Paar der Form .
Da Funktionen von nach aus genau drei Paaren bestehen müssen, sind übrigens auch und keine Funktionen von nach .
-
ist eine Funktion von nach , denn jeder natürlichen Zahl n ist genau eine natürliche Zahl, und zwar die um 2 größere, zugewiesen.
-
Die Menge ist keine Funktion von nach , denn das zu ihr gehörende Paar liegt nicht in .
|
Oft besteht eine Funktion f aus sehr vielen Paaren. Statt nun diese Paare alle einzeln aufzuführen, ist es bequemer, sie in tabellarischer Form zu notieren, also eine Wertetabelle zu erstellen.
Die Funktion aus dem ersten Beispiel kann durch die folgende Wertetabelle sogar vollständig angegeben werden:
Natürlich lässt sich eine Funktion nur dann durch eine Wertetabelle vollständig angeben, wenn der Definitionsbereich endlich ist. Eine Wertetabelle für die Funktion aus dem vierten Beispiel kann also immer nur ein Auszug sein. Außerdem ist hier - anders als im ersten Beispiel - bereits eine Funktionsvorschrift erkennbar, so dass man in der Tafel statt , bzw. , besser gleich n + 2 schreibt:
Eine Wertetabelle gibt schnell einen groben Überblick über eine Funktion. Wesentlich aufschlussreicher allerdings ist ihre graphische Darstellung. Möglich ist dies oft, falls eine Teilmenge von (oder auch von ) ist,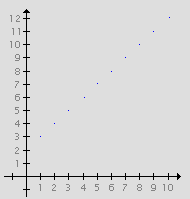 denn dann ist eine Funktion f eine Teilmenge der Zeichenebene (bzw. des Raumes) und ihr Graph entsteht durch Markieren alle Paare der Form . f ist aber genau die Menge dieser Paare, so dass der oft gemachte Unterschied zwischen einer Funktion und ihrem Graphen in Wirklichkeit nicht vorhanden ist. Wir werden dennoch an diesem Sprachgebrauch festhalten und den Begriff Funktion eher mit dem Festlegen der Funktionsvorschrift und den Begriff Graph eher mit dem Anfertigen einer Skizze verbinden. denn dann ist eine Funktion f eine Teilmenge der Zeichenebene (bzw. des Raumes) und ihr Graph entsteht durch Markieren alle Paare der Form . f ist aber genau die Menge dieser Paare, so dass der oft gemachte Unterschied zwischen einer Funktion und ihrem Graphen in Wirklichkeit nicht vorhanden ist. Wir werden dennoch an diesem Sprachgebrauch festhalten und den Begriff Funktion eher mit dem Festlegen der Funktionsvorschrift und den Begriff Graph eher mit dem Anfertigen einer Skizze verbinden.
So ist etwa die Funktion aus dem vierten Beispiel als Teilmenge von auch eine Teilmenge von , also graphisch darstellbar. Die nebenstehende Skizze zeigt die ersten zehn Paare dieser Funktion. Man beachte, dass der Graph hier nur aus Gitterpunkten besteht, dies ist aber durch bedingt.
Eine Funktion als Menge ihrer Paare anzugeben, ist zwar völlig korrekt, aber im "mathematischen Alltag" nicht gebräuchlich. Insbesondere wenn die Funktionswerte über eine Rechenvorschrift (mit eindeutigen Ergebnissen) ermittelt werden, benutzt man eine leichter zu lesende Form der Funktionsangabe:
Ist f eine Funktion von A nach B, so notieren wir dies mit dem Symbol
und geben anschließend die Funktionswerte an. Das folgende Beispiel stellt dies vor und erläutert zudem ausführlich die zu einer Funktion gehörenden Begriffe.
|
Beispiel: Statt also festzusetzen: Sei , schreiben wir: Die Funktion
sei gegeben durch .
Gelegentlich will man den Zuordnungscharakter stärker betonen; man ersetzt dann die Zuordnungvorschrift durch das Symbol (lies: "x geht auf ").
Wir berechnen nun einige Funktionswerte, und zwar durch Einsetzen. So ist z.B.
Das Ermitteln von Urbildern führt zu einer anderen Aufgabenstellung: Die Frage etwa, ob die Zahl 15 Urbilder besitzt, führt zur Suche nach Zahlen x, so dass gilt, also zur Gleichung , die man zu löst. 15 besitzt damit zwei Urbilder, nämlich 4 und −4. Die Gleichung dagegen hat keine Lösung, −2 also auch keine Urbilder. Andererseits aber gehört −2 zum angegebenen Bildbereich, so dass in diesem Fall Bild- und Wertebereich auseinander fallen.
Welchen Wertebereich aber besitzt die Funktion f ? Da stets positiv ist, hat man zunächst für alle Funktionswerte:
, also ist der Wertebereich eine Teilmenge von . Ist nun andererseits y irgendein Element von , also , so kann man aus die Wurzel ziehen. Folgt:
. y ist also als Funktionswert darstellbar. Damit ist der Wertebereich auch eine Obermenge von , und somit gleich .
Schließlich fertigen wir eine Skizze der Funktion f an. Dazu erstellen wir zunächst eine Wertetabelle:
und tragen die so gewonnenen Daten in die nebenstehende Skizze ein. Durch Klicken auf die Zeiger kann man nun die Anzahl der eingetragenen Punkte verändern und so die Entstehung des Graphen verfolgen.
|
In den folgenden Abschnitten werden wir viele Funktionen von nach ausführlich behandeln. Hier möchte ich abschließend einige Beispiele zeigen, die die Variationsbreite des Funktionsbegriffs illustrieren.
|
Beispiel:
-
Die Funktion sei gegeben durch
. f ordnet jedem Zahlenpaar das Entfernungsquadrat seines Abstands zum Ursprung zu, also z.B:
Der
Graph von f ist eine Fläche im . von f ist eine Fläche im .
i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Display by JavaView
|
|
Die hier vorgestellte Funktion f ist symmetrisch: Bei der Berechnung von Funktionswerten kommt es auf die Reihenfolge der beiden Zahlen x und y nicht an:
Die beiden folgenden Beispiele zeigen zwei weitere symmetrische Funktionen, die beiden sog. elementarsymmetrischen Funktionen des .
|
Beispiel:
-
Die Funktionen definieren wir durch
Da + und · kommutativ sind, ist die Symmetrie von und gewährleistet. Wir notieren eine kleine Wertetabelle und sehen uns die Graphen an:
|
|

i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Display by JavaView
|

i   |
| Linke Maustaste: Rotieren | Rechte Maustaste: Kontextmenü |
Display by JavaView
|
|
und spielen im Zusammenhang mit dem Satz von Viëta eine interessante Rolle, man kann sie nämlich zu seiner Formulierung verwenden:
a und b lösen die Gleichung .
Der Vorteil dieser ungewöhnlichen, "komplizierteren" Darstellung des Viëtaschen Satzes ist ihre Erweiterbarkeit. In einem Exkurs ist das ausführlich dargestellt.
|
Die letzten drei Beispielen sind überhaupt nicht mehr zu visualisieren.
|
Beispiel:
-
Für die Funktion , gegeben durch
,
erhalten wir die folgende Wertetabelle:
f ist eine Teilmenge des , an eine Skizze des Graphen ist also nicht zu denken.
-
Funktionen zwischen den komplexen Zahlen lassen sich überhaupt nicht graphisch darstellen. Wir betrachten die komplexe Quadratfunktion , gegeben duch
, bzw.
und berechnen einige Funktionswerte:
-
Wir ordnen jeder nicht-leeren Teilmenge von , also den nicht-leeren Elementen der Potenzmenge

i   |
|
Die Potenzmenge einer Menge M ist die Gesamtheit aller Teilmengen von M. Also:
.
In einer Mengenlehre mit Potenzmengenaxiom ist wieder eine Menge und es gilt die Äquivalenz
.
So ist etwa . Man beachte, dass die Aussage stets zutrifft.
|
von , das kleinste in ihr enthaltene Element zu. Da durch die Relation total geordnet ist, besitzt jedes , genau ein kleinstes Element, d.h. durch die Festsetzung
ist eine Funktion gegeben. Hier ein kleiner Überblick:
Da das Minimum von A stets Element von A ist, besitzt die Funktion f die Eigenschaft:
für jede nicht-leere Teilmenge A von . f wählt also in einer bestimmten Weise, nämlich über die Bildung des Minimums, aus jedem A ein Element aus. f nennt man deshalb auch eine Auswahlfunktion für .
Die Frage, ob jede Menge M eine Auswahlfunktion besitzt, ist nicht trivial und letztlich nur über ein Axiom zu entscheiden: Betreibt man eine Mengenlehre mit Auswahlaxiom, so gibt es zu jeder Menge eine Auswahlfunktion. In anderen Mengenlehren ist dies falsch.
|
|
 |
|

 denn dann ist eine Funktion f eine Teilmenge der Zeichenebene (bzw. des Raumes) und ihr Graph entsteht durch Markieren alle Paare der Form . f ist aber genau die Menge dieser Paare, so dass der oft gemachte Unterschied zwischen einer Funktion und ihrem Graphen in Wirklichkeit nicht vorhanden ist. Wir werden dennoch an diesem Sprachgebrauch festhalten und den Begriff Funktion eher mit dem Festlegen der Funktionsvorschrift und den Begriff Graph eher mit dem Anfertigen einer Skizze verbinden.
denn dann ist eine Funktion f eine Teilmenge der Zeichenebene (bzw. des Raumes) und ihr Graph entsteht durch Markieren alle Paare der Form . f ist aber genau die Menge dieser Paare, so dass der oft gemachte Unterschied zwischen einer Funktion und ihrem Graphen in Wirklichkeit nicht vorhanden ist. Wir werden dennoch an diesem Sprachgebrauch festhalten und den Begriff Funktion eher mit dem Festlegen der Funktionsvorschrift und den Begriff Graph eher mit dem Anfertigen einer Skizze verbinden.