7.4. Lokale Aspekte
Analog zur Stetigkeit erweist sich auch die Differenzierbarkeit in a als eine lokale Eigenschaft. Sie ist also u.a. einschränkungstreu:
|
Bemerkung: Sei
ein Häufungspunkt von A (und damit auch von B) und . Ist f in a differenzierbar, so ist auch differenzierbar in a mit derselben Ableitung:
|
[7.4.1] |
Die Umkehrung ist auch hier i.a. falsch: Nach einem Beispiel in 7.3 ist die Betragsfunktion in 0 nicht differenzierbar, ihre Einschränkung dagegen schon.
Beweis: Die Behauptung folgt direkt aus [6.9.1], denn
die Differenzenquotientenfunktion zu ist eine Einschränkung der Differenzenquotientenfunktion zu f:
|
So hat man z.B. für jede Teilmenge A von mit als Häufungspunkt:
und
Der lokale Charakter der Differenzierbarkeit zeigt sich auch im Verhalten lokal identischer Funktionen.
Bemerkung:
sei ein Häufungspunkt von . Sind und in a
lokal identisch
i  |
|
d.h. es gibt zwei relative ε-Umgebungen
so dass und für alle .
|
, so gilt:
f ist differenzierbar in a
g ist differenzierbar in a.
|
[7.4.2] |
Im Differenzierbarkeitsfall hat man zusätzlich: .
Beweis:
Mit f und g sind auch die Differenzenquotientenfunktionen und in a lokal identisch. Nach [6.9.2] ist genau dann in a stetig fortsetzbar,
wenn dies auf zutrifft. In diesem Fall haben darüber hinaus beide Differenzenquotientenfunktionen denselben Grenzwert.
|
Beachte:
Da f und in a immer lokal identisch sind, gestattet es [7.4.2], Untersuchungen zur Differenzierbarkeit nur lokal zu führen:
f ist differenzierbar in a ist differenzierbar in a für ein
Existieren die Ableitungszahlen, sind sie identisch: .
[7.4.2] ist insbesondere ein elegantes Werkzeug bei der Untersuchung abschnittsweise definierter Funktionen. Wir zeigen dies im folgenden Beispiel für die Betragsfunktion.
Beispiel:
Die Betragsfunktion ist in jedem
differenzierbar. Dabei gilt für die Ableitungszahl
|
[7.4.3] |
Beweis:
Für
ist lokal identisch mit X, besitzt also hier die Ableitungszahl 1.
Für
ist lokal identisch mit −X, besitzt also hier die Ableitungszahl −1.
|
Nach dem oben erwähnten Beispiel aus 7.3 ist die Betragsfunktion in 0 nicht differenzierbar. [7.4.3] belegt also, dass sie in nur einem einzigen Punkt nicht differenzierbar ist.
Das folgende Beispiel dagegen stellt eine Funktion vor, die in ausschließlich einem Punkt differenzierbar ist. Beide Beispiele zeigen, dass das Differenzierbarkeitsverhalten in einem Punkt keinen Einfluss auf das Verhalten in den Nachbarpunkten hat.
|
Beispiel: Die Funktion
, also
|
[7.4.4] |
ist in 0 differenzierbar. In jedem ist sie nicht differenzierbar.
Beweis:
Für alle hat man die Abschätzung
Nach [6.9.10]/[6.9.11] ist f damit in 0 differenzierbar und . Wäre f in einem differenzierbar, so wäre sie dort auch stetig (siehe [7.5.2]) und damit auch die Funktion , im Widerspruch zu [6.2.15].
|
Zu den lokalen Aspekten gehört auch die Frage nach der Verklebbarkeit (siehe [6.8.7]), hier der differenzierbaren Verklebbarkeit, zweier Funktionen. Die folgende Bemerkung zeigt, dass zwei Funktionen differenzierbar verklebt werden können sobald ihre Funktions- und Ableitungswerte in a identisch sind.
|
Bemerkung: und seien zwei Funktionen mit , ein Häufungspunkt sowohl von A wie auch auch von B. Dann gilt:
|
ist differenzierbar in a |
| f und g sind in a differenzierbar mit |
|
[7.4.5] |
Beweis: "" folgt mit [7.4.1] direkt aus den Gleichheiten und .
"": Gemäß Voraussetzung ist für alle
Man hat also , und da folgt mit [6.8.9]:
ist in a stetig fortsetzbar. Also ist in a differenzierbar mit als Ableitungszahl.
|
|
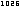 |
|