7.3. Differenzierbare Funktionen
Auch in diesem Abschnitt orientieren wir uns an dem in 7.1. gewonnenen Ergebnis. Mit den Differenzenquotientenfunktionen haben wir für das Spektrum
der Sekantensteigungen eine passende mathematische Beschreibung gefunden. Hier nun werden wir, mit [7.1.2] als Vorgabe, die Tangentensteigung selbst definieren.
|
Definition: Es sei
ein Häufungspunkt von .
Eine Funktion heißt differenzierbar in a, falls die
Differenzenquotientenfunktion
in a stetig fortsetzbar ist. In diesem Fall nennen wir die reelle Zahl
|
[7.3.1] |
die Ableitung (genauer: die Ableitungszahl) von f in a.
|
Beachte:
Als Grenzwert der Sekantensteigungen interpretieren wir
als die
Steigung der Tangente an f im Punkt (a, f(a)). Da a ein Häufungspunkt von A - und damit auch von
- ist,
besitzt höchstens eine stetige Fortsetzung in a. Ihr Limes in a, d.h. die
Zahl ist daher eindeutig bestimmt.
Das Symbol geht auf Cauchy zurück und ist heute weit verbreitet. Gebräuchlich ist aber auch die von Leibniz eingeführte Schreibweise oder auch für die Ableitungszahl. Sie entstammt der Vorstellung, dass im Grenzprozess der Quotient der Differenzen und in den
mystischen
i  |
|
Man beachte, dass Leibniz (1646 - 1716) noch nicht über einen präzisen Grenzwertbegriff verfügen konnte. Erst Cauchy (1789 - 1857) selbst entwickelte hier ein mathematisch befriedigendes Konzept.
|
Quotienten der Differentiale df und dx übergeht. lesen wir als "df nach dx" um, zumindest sprachlich, die Verwechselung mit einem wirklichen Quotienten auszuschließen. -
Auch hier hat die Physik eine eigene Notation: Für Funktionen, die die Zeit als Argument verwenden, also etwa Funktionen des Typs (vgl. dazu die Anmerkung in [7.2]) bezeichnet man die Ableitungszahl mit einem Punktsymbol
und nennt sie die Momentangeschwindigkeit (auch: lokale Geschwindigkeit) zum Zeitpunkt . In der Regel schreibt man dann: .
Aus diesem Sprachfeld stammt auch die Bezeichnung "momentane Änderungsrate der Funktion f im Punkt a" für die Ableitungszahl .
Beispiel:
-
Jede lineare Funktion ist in jedem
differenzierbar und
►
| [7.3.2] |
denn nach [7.2.2] ist in a stetig fortsetzbar durch die konstante
Funktion m auf .
Damit ergibt sich nun:
.
-
Für ist die Potenzfunktion in jedem differenzierbar und
►
| [7.3.3]
|
denn nach [7.2.3] ist in a stetig fortsetzbar durch . Für die Ableitungszahl bedeutet dies:
.
-
Die Kehrwertfunktion ist in jedem differenzierbar und
►
| [7.3.4] |
denn gemäß [7.2.4] ist
die stetige Fortsetzung von in a. Also berechnet sich die Ableitungszahl zu
.
-
Die Wurzelfunktion ist in jedem
differenzierbar und
►
|
[7.3.5] |
denn nach [7.2.5] wird in a stetig fortgesetzt durch
, also ist
.
-
Die Wurzelfunktion ist nicht differenzierbar in 0. Ihre Differenzenquotientenfunktion ist in 0 nicht stetig fortsetzbar, denn so ist z.B.
eine Nullfolge in , ihre Bildfolge
aber ist divergent.
-
Die Betragsfunktion ist in 0 nicht differenzierbar:
(siehe [7.2.6]) läßt keine stetige Fortsetzung in 0 zu.
Dazu betrachte man die Nullfolge
in ; ihre Bildfolge
ist divergent.
|
Beachte:
Am Beginn unserer Überlegungen stand die Suche nach Tangenten. Das Hauptproblem, das Finden der richtigen Steigung,
ist mit den Ableitungszahlen gelöst worden. Wir können also nun Tangenten errechnen.
Definition:
Ist in
differenzierbar, so heißt die Funktion
|
[7.3.7] |
die zu f gehörige Tangentenfunktion bzgl. a.
|
Beachte:
Gelegentlich schreiben wir statt um deutlicher auf die Zugehörigkeit zu f hinzuweisen.
ist eine lineare Funktion, die den Graphen von f im Punkt (a, f(a)) trifft, denn , und
als Steigungszahl hat.
Unabhängig von A ist der Definitionsbereich der Tangentenfunktionen immer ganz .
Ergänzend zur Tangente interessiert man sich oft für die sog. Normale, d.h. für die durch (a, f(a)) gehende Senkrechte zur Tangenten. Eine nicht senkrechte Normale können wir durch eine lineare Funktion beschreiben:
|
Definition: Ist in
differenzierbar mit , so heißt die Funktion
|
[7.3.8] |
die zu f gehörige Normalenfunktion bzgl. a.
|
Beachte:
Für die Normalenfunktion benutzen wir, wenn nötig, auch die erweiterte Notation . Da geht tatsächlich durch (a, f(a)). Ihre Steigung ist der Kehrwert der Steigung von mit vertauschtem Vorzeichen. steht daher
senkrecht
i  |
|
Ist g eine Gerade mit einer von Null verschiedenen Steigungszahl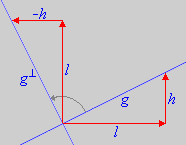 , so besitzt die durch Drehung um 90° entstehende zu g senkrechte Gerade die Steigung , so besitzt die durch Drehung um 90° entstehende zu g senkrechte Gerade die Steigung
|
auf . Unabhängig von A ist der Definitionsbereich der Normalenfunktion immer ganz .
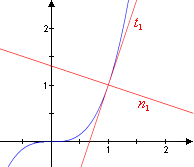
Als Beispiel berechnen wir die Tangenten- und die Normalenfunktion zur Kubikfunktion bzgl. 1. Mit und erhält man
|
 |
Aufgabe: Berechne die Tangenten- und Normalenfunktionen zu
bzgl. 4:
-
bzgl. −1:
-
bzgl. a:
|
Gelegentlich ist es von Vorteil, die Tangente als eine Gerade in vektorieller Schreibweise zu notieren. Dazu benötigt man nur einen Geradenpunkt, hier bietet sich natürlich (a, f(a)) an, sowie einen Richtungsvektor. Dazu beachte man, dass bei einem Längenzuwachs von 1 der Wert den entsprechenden Höhenzuwachs angibt. Also hat man:
|
[7.3.9] |
Ferner steht der Vektor senkrecht auf so dass die Normale in der Form
|
[7.3.10] |
notiert werden kann. Die Darstellung [7.3.10] hat zudem den Vorteil, dass mit ihr auch eine senkrechte Normale beschrieben werden kann. Im nicht senkrechten Fall beachte man aber, dass die Vektoren und dieselbe Richtung repräsentieren.
Als Beispiel betrachten wir noch einmal im Punkt 1. besitzt hier die Tangente und die Normale .
|
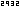 |
|
 , so besitzt die durch Drehung um 90° entstehende zu g senkrechte Gerade die Steigung
, so besitzt die durch Drehung um 90° entstehende zu g senkrechte Gerade die Steigung