9.13. Skalarprodukte

- - - - - Diese Seite braucht webEQ! Klicken Sie auf das Logo. - - - - -

9.13. Skalarprodukte

Wir wenden uns nun verstärkt geometrischen Aspekten zu: In diesem Abschnitt entwickeln wir Konzepte zur Längen- und zur Winkelmessung, im nächsten Abschnitt wird das Prinzip des zu einander Senkrechtstehens, der Orthogonalität, untersucht.

Zur Einführung geometrischer Begriffe benötigt man allerdings zusätzliche Strukturen. Als eine einheitliche Grundlage erweisen sich dabei die Skalarprodukte. Wir stellen sie zunächst vor.

Definition: Es sei (V, + , · ) ein Vektorraum. Eine Funktion

* : V ´ V ® R

heißt ein Sakalarprodukt (bzw. ein inneres Produkt) auf V, falls

v * w = w * v für alle v,w Î V.
(v₁ + v₂) * w = (v₁ * w) + (v₂ * w) für alle v_i,w Î V.
(av) * w = a(v * w) für alle v,w Î V und a Î R .
v * v > 0 für alle v Î V, v ¹ 0.

V heißt euklidischer Vektorraum, wenn auf V ein Skalarprodukt * gegeben ist. Wir notieren einen euklidischen Vektorraum als 4-Tupel: (V, + , · , * ).

Beachte:

* ist also genau dann ein Skalarprodukt, wenn *
- kommutativ ist (Eigenschaft 1),
- in der ersten Koordinate linear ist (Eigenschaften 2 und 3),
- positiv definit ist (Eigenschaft 4).
Zur Einsparung von Klammern vereinbaren wir, dass das Skalarprodukt stärker binden soll als Addition und Subtraktion, aber schwächer als die skalare Multiplikation. 2. und 3. läßt sich damit kürzer formulieren:

(v₁ + v₂) * w = v₁ * w + v₂ * w
av * w = a(v * w).
Wenn die Rechenoperationen und das Skalarprodukt festliegen, schreiben wir meist V statt (V, + , · , * ).
Ist U Untervektorraum eines euklidischen Vektorraums (V, + , · , * ), so ist * auch ein Skalarprodukt auf U; (U, + , · , * ) ist also ebenfalls ein euklischer Raum.

Ein Skalarprodukt ist in beiden Koordinaten linear. Es ist daher breits eindeutig bestimmt, wenn man seine Werte auf den Vektoren einer vorgegebenen Basis kennt. Umgekehrt läßt sich dieses Verhalten nutzen, um jeden Vektorraum mit einem Skalarprodukt zu versehen, ihn also (auf mindestens eine Weise) zu einem euklidischen Vektorraum zu machen.

Bemerkung und Bezeichnung: Es sei V ein Vektorraum, B Ì V eine Basis von V mit zugehöriger Koordinatentransformation T_B. Für jede Funktion

j : B ® R ^>⁰

wird durch die Festsetzung

x_{*_{B, ϕ}} y : = \sum_{v \in B} T_{B} (x) (v) T_{B} (y) (v) ϕ (v)

ein Skalarprodukt auf V erklärt. Dabei gilt für Basiselemente a,b Î B: $a_{*_{B, ϕ}} b = {\begin{array}{l} ϕ (a),&quad;falls a = b \\ 0,&quad;falls a \neq b \end{array}$ .

Setzt man abkürzend a := T_B(x) und b := T_B( y), so läßt sich die Definition übersichtlicher notieren:

x_{*_{B, ϕ}} y = \sum_{v \in B} α (v) β (v) ϕ (v)

Ist speziell j = 1, so nennt man das Skalarprodukt *_B,₁ das zu B gehörige Standardskalarprodukt.

Beweis: Wesentliches Argument ist (in 2. und 3.) die Linearität von T_B.

$&quad; 1.&quad; x_{*_{B, ϕ}} y = \sum_{v \in B} T_{B} (x) (v) T_{B} (y) (v) ϕ (v) = \sum_{v \in B} T_{B} (y) (v) T_{B} (x) (v) ϕ (v) = y_{*_{B, ϕ}} x$ .

$\begin{array}{l} &quad; 2.&quad; {(x + y)}_{*_{B, ϕ}} z & = \sum_{v \in B} T_{B} (x + y) (v) T_{B} (z) (v) ϕ (v) \\ = \sum_{v \in B} T_{B} (x) (v) T_{B} (z) (v) ϕ (v) + \sum_{v \in B} T_{B} (y) (v) T_{B} (z) (v) ϕ (v) \\ = x_{*_{B, ϕ}} z + y_{*_{B, ϕ}} z . \end{array}$

$&quad; 3.&quad; {α x}_{*_{B, ϕ}} y = \sum_{v \in B} T_{B} (α x) (v) T_{B} (y) (v) ϕ (v) = α \sum_{v \in B} T_{B} (x) (v) T_{B} (y) (v) ϕ (v) = α (x_{*_{B, ϕ}} y)$ .

4. Zu jedem x ¹ 0 gibt es ein v_x Î B, so dass T_B(x)(v_x) ¹ 0. Da ferner j(v) > 0 für alle v hat man also:

x_{*_{B, ϕ}} x = \sum_{v \in B} {(T_{B} (x) (v))}^{2} ϕ (v) \geq {(T_{B} (x) (v_{x}))}^{2} ϕ (v_{x}) > 0

Bleibt der Zusatz über die Basisvektoren. Dabei beachte man zunächst, dass für den Koordinatenvektor eines a Î B gilt:

T_B(a) = c_{_a_}.

Damit ergibt sich

$a_{*_{B, ϕ}} a = \sum_{v \in B} T_{B} (a) (v) T_{B} (a) (v) ϕ (v) = \sum_{v \in B} χ_{{a}} (v) χ_{{a}} (v) ϕ (v) = ϕ (a)$ .
Und für a ¹ b: $a_{*_{B, ϕ}} b = \sum_{v \in B} T_{B} (a) (v) T_{B} (b) (v) ϕ (v) = \sum_{v \in B} χ_{{a}} (v) χ_{{b}} (v) ϕ (v) = 0$ .

Wir geben nun einige konkrete Beispiele für ein Skalarprodukt an.

Beispiel:

In Rⁿ ist das in 9.9 eingeführte Skalarprodukt × ein Skalarprodukt. (Rⁿ, + , · , × ) ist somit euklidischer Vektorraum.
In R³ ist durch

x * y := x₁y₁ + 2x₂y₂ + 3x₃y₃ + x₁y₃ + x₃y₁

ein Skalarprodukt erklärt.
In C ⁰([a,b]) wird durch die Festsetzung

$f_{*} g : = \int_{a}^{b} f g$
ein Skalarprodukt erklärt.

d.	Im Quotientenraum	F_konv (N )	/	F_0-konv (N )	erklären wir ein Skalarprodukt über die Limesbildung:
	((a_n) + F_0-konv (N )) * ((b_n) + F_0-konv (N )) := lim a_nb_n.

Beweis:

Zu b.: Die Kommutativität von * ist offensichtlich. Zu den weiteren Eigenschaften:

(x + y) * z	= (x₁ + y₁)z₁ + 2(x₂ + y₂)z₂ + 3(x₃ + y₃)z₃ + (x₁ + y₁)z₃ + (x₃ + y₃)z₁
	= x₁z₁ + y₁z₁ + 2x₂z₂ + 2y₂z₂ + 3x₃z₃ + 3y₃z₃ + x₁z₃ + y₁z₃ + x₃z₁ + y₃z₁
	= x₁z₁ + 2x₂z₂ + 3x₃z₃ + x₁z₃ + x₃z₁ + y₁z₁ + 2y₂z₂ + 3y₃z₃ + y₁z₃ + y₃z₁
	= x * z + y * z.

a x * y	= a x₁y₁ + 2a x₂y₂ + 3a x₃y₃ + a x₁y₃ + a x₃y₁
	= a(x₁y₁ + 2x₂y₂ + 3x₃y₃ + x₁y₃ + x₃y₁)
	= a (x * y).

x * x	= x₁x₁ + 2x₂x₂ + 3x₃x₃ + x₁x₃ + x₃x₁
	= x₁² + 2x₂² + 3x₃² + 2x₁x₃
	= (x₁ + x₃)² + 2x₂² +2x₃².

x * x ist also eine Summe von Quadraten und damit stets ³ 0. Sei nun x ¹ 0. Ist x₂ ¹ 0 oder x₃ ¹ 0, so hat man sofort x * x > 0. Sind x₂ und x₃ beide gleich 0, so muß x₁ ¹ 0 sein und damit ist x * x = (x₁ + x₃)² = x₁² > 0.

Zu c.: Man beachte, dass * wohldefiniert ist, denn mit f und g ist auch fg stetig, also über [a,b] integrierbar. Die Kommutativität von * ist offensichtlich. Die Linearität in den Koordinaten ergibt sich aus dem Distributivgesetz und der Linearität des Integrals.
Bleibt, die positive Definitheit zu zeigen. Sei dazu f Î C ⁰([a,b]), f ¹ 0. Also gibt es ein y Î [a,b], so dass f( y) ¹ 0 ist. Aus Stetigkeitsgründen ist f dann in einer Umgebung von y ungleich 0: es gibt daher ein Intervall [c,d], so dass y Î [c,d] Ì [a,b] und f(x) ¹ 0 für alle x Î [c,d]. Da das Integrieren monoton ist, kann man nun folgendermaßen abschätzen:

f_{*} f = \int_{a}^{b} f^{2} \geq \int_{c}^{d} f^{2} > 0

Zu d.: Zunächst stellen wir sicher, dass * wohldefiniert ist. Ist etwa

(a_n) + F_0-konv (N ) = (a'_n) + F_0-konv (N )
(b_n) + F_0-konv (N ) = (b'_n) + F_0-konv (N ),

so sind (a_n) - (a'_n) und (b_n) - (b'_n) Nullfolgen. Das bedeutet:

lim a_n = lim a'_nlim b_n = lim b'_n,

also ist lim a_nb_n = lim a'_nb'_n.

Beachte:

× aus a. ist das zur Standardbasis {e₁,...,e_n} gehörige Standardskalarprodukt:

$ċ =_{*_{{e_{1}, . . . , e_{n}}, 1}}$ .

Man hat also insbesondere: e_i × e_j = d_ij.

Wir werden im Folgenden den Rⁿ stets mit diesem Skalarprodukt versehen. Allerdings zeigt das Beispiel b. dass Rⁿ auch andere Skalarprodukte tragen kann.
In R¹ = R ist das Standardskalarprodukt die gewöhnliche Multiplikation.
* in c. ist das klassische Skalarprodukt auf C ⁰([a,b]).
Der Versuch das Skalarprodukt in d. "nur" auf F_konv (N ) und nicht auf dem Quotientenraum einzuführen, also

(a_n) * (b_n) := lim a_nb_n,

zu setzen, scheitert (nur) an der positiven Definitheit:
Zwar ist $(\frac{1}{n}) \neq 0, aber: (\frac{1}{n})_{*} (\frac{1}{n}) = lim \frac{1}{n^{2}} = 0$ .

Das nachfolgende allgemeine Beispiel ermöglicht es, Skalarprodukte zu "importieren", also gewissermaßen eine euklidische Struktur von einem Vektorraum auf einen anderen zu übertragen.

Beispiel und Bezeichnung: Es sei V ein Vektorraum und W ein euklidischer Vektorraum. Ist f : V ® W linear und injektiv (also ein injektiver Homomorphismus), so wird durch

v *_f w := f(v) * f(w)

ein Skalarprodukt auf V definiert. *_f heißt das durch f induzierte Skalarprodukt auf V.

Beweis:

v *_f w = f(v) * f(w) = f(w) * f(v) = w *_f v.
(v₁ + v₂) *_f w = f(v₁ + v₂) * f(w) = ( f(v₁) + f(v₂)) * f(w) = f(v₁) * f(w) + f(v₂) * f(w) = v₁ *_f w + v₂ *_f w.
(av) *_f w = f(av) * f(w) = a f(v) * f(w) = a( f(v) * f(w)) = a(v *_f w) .
Ist v ¹ 0, so ist wegen der Injektivität von f auch f(v) ¹ 0. Daraus folgt: v *_f v = f(v) * f(v) > 0.

Aus den definierenden Eingenschaften des Skalarprodukts ergben sich weitere:

Bemerkung: Es sei V ein euklidischer Vektorraum. Dann gilt für alle v,v_i,w Î V und a Î R :

v * (w₁ + w₂) = v * w₁ + v * w₂
v * aw = a(v * w)
(v₁ - v₂) * w = v₁ * w - v₂ * w
v * (w₁ - w₂) = v * w₁ - v * w₂
0 * w = v * 0 = 0
I.a. gilt nicht: v * w = 0 Þ v = 0 Ú w = 0

Beweis:

Zu 1.: Mit der Kommutativität und der Linearität in der ersten Koordinate von * kann man wie folgt argumentieren:

v * (w₁ + w₂) = (w₁ + w₂) * v = w₁ * v + w₂ * v = v * w₁ + v * w₂.

Zu 2.: 2. wird wie gerade bewiesen.

Zu 3.: Wir zeigen nur die erste Gleichung (die zweite ergibt sich wieder nach dem Schema zu 1.):

(v₁ - v₂) * w = (v₁ + (-v₂)) * w = v₁ * w + (-v₂) * w = v₁ * w + (-(v₂ * w)) = v₁ * w - v₂ * w.

Zu 4.: 0 * w = (0·0) * w = 0(0 * w) = 0.

Zu 5.: Z.B. ist in R²: e₁ * e₂ = 0.

Euklidische Vektorräume ermöglichen die Einführung geometrischer Strukturen. In diesem Abschnitt betrachten wir zwei grundlegende Konzepte: die Längen- und die Winkelmessung.

Wir beginnen mit der Längenmessung und orientieren uns dabei an den geometrischen Verhältnissen des Rⁿ.

Stellt man sich unter der Länge eines Vektors x die Länge
des durch x gegebenen Pfeils vor, so kann man, etwa in R²,
diese Länge über den Satz des Pythagoras errechnen:

$\sqrt{x_{1}^{2} + x_{2}^{2}} = \sqrt{x ċ x}$ .

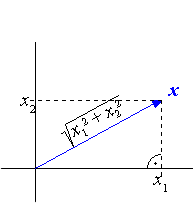Definition: Es sei V ein euklidischer Vektorraum. Für v Î V setzen wir

$| v | : = \sqrt{v ċ v}$ .

Die Zahl | v | heißt die Länge (bzw. die Norm) des Vektors v. Ist | v | = 1, so nennen wir v einen Einheitsvektor.

Beachte:

Da das Skalarprodukt * ist positiv definit ist, hat man stets: v * v ³ 0. Also ist die Länge | v | wohldefiniert.
Statt v * v schreiben wir abkürzend auch v², also auch: $| v | = \sqrt{v^{2}}$ ; damit hat man offensichtlich:

v² = | v |².
Benutzt man den Ausdruck Norm von v, so ersetzt man das Symbol | v | oft durch || v ||.
In Rⁿ ist $| x | = \sqrt{\sum_{i = 1}^{n} x_{i}^{2}}$ , so dass wir gemäß Pythagoras die Länge des Vektors x als den Nullabstand des Punktes x im Koordinatensystem interpretieren dürfen.
In R¹ = R ist die Länge des Vektors x = (x) gleich dem Betrag der Zahl x: $| x | = \sqrt{x^{2}} = | x |$ .

Beispiel: Wir berechnen die Längen einiger Vektoren

in Rⁿ:
- $| (\begin{matrix} 3 \\ - 4 \end{matrix}) | = \sqrt{(\begin{matrix} 3 \\ - 4 \end{matrix}) ċ (\begin{matrix} 3 \\ - 4 \end{matrix})} = \sqrt{9 + 16} = 5$ .
- $| (\begin{matrix} \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \end{matrix}) | = \sqrt{(\begin{matrix} \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \end{matrix}) ċ (\begin{matrix} \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \\ \overset{1}{} \underset{&!; / &!; \sqrt{3}}{} \end{matrix})} = \sqrt{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}} = 1$ .
in C ⁰([0,1]):
- $| X^{2} | = \sqrt{X^{2} * X^{2}} = \sqrt{\int_{0}^{1} X^{4}} = \frac{1}{\sqrt{5}}$ .
- $| c | = \sqrt{c_{*} c} = \sqrt{\int_{0}^{1} c^{2}} = | c |$ .

c.	in F_konv (N )	/	F_0-konv (N )	^{^:}
	\| $(\frac{2 n}{n + 1})$ + F_0-konv (N ) \| $= lim (\frac{2 n}{n + 1}) (\frac{2 n}{n + 1}) = 4$ .

Bemerkung: Es sei V ein euklidischer Vektorraum. Dann gilt für alle v,w Î V und a Î R :

| v | ³ 0

| v | = 0   Û   v = 0

| av | = | a | | v |

| v | = | -v |

| v * w | £ | v |·| w |   ("Cauchy-Schwarzsche Ungleichung")

| v * w | = | v |·| w |   Û   v,w linear abhängig

| v + w | £ | v | + | w |          ("Dreiecksungleichung")

| v - w | ³ | v | - | w |          ("Zweite Dreiecksungleichung")

| v + w |² + | v - w |² = 2| v |² + 2| w |²          ("Parallelogrammgesetz")

Beweis:

Zu 1.: Dies ist eine Eigenschaft der Wurzel: $| v | = \sqrt{v^{2}} \geq 0$ .

Zu 2.: Für diese "Þ" Richtung benötigen wir ebenfalls eine Wurzeleigenschaft:
Ist nämlich v ¹ 0, so ist v * v > 0, also hat man auch $| v | = \sqrt{v^{2}} > 0$ .
Die Richtung "Ü" ergibt sich sofort aus 0 * 0 = 0.

Zu 3.: Es reicht, die Gleichheit der Quadrate festzustellen:

| av |² = av * av = a·a(v * v) = a²v² = | a |²| v |² = (| a | | v |)².

Zu 4.: Die Behauptung folgt mit a = -1 direkt aus 3.

Zu 5.: Für w = 0 ist nichts zu zeigen; sei also w ¹ 0. Der Beweis ist jetzt ein wenig trickreich. Neben einigen Eigenschaften des Skalarprodukts benötigen wir am Ende das Monotonieverhalten der Wurzelfunktion. Wir setzen nun $c : = \frac{v_{*} w}{| w |^{2}}$ und zeigen der Reihe nach:

0 £ (v - cw) * (v - cw)

= v * v - 2c(v * w) + c²(w * w)

= | v |² - 2c(v * w) + c²| w |²

= ${| v |}^{2} - 2 \frac{{(v_{*} w)}^{2}}{| w |^{2}} + \frac{{(v_{*} w)}^{2}}{| w |^{2}}$

Þ     0 £ | v |²·| w |² - 2(v * w)² + (v * w)²

= | v |²·| w |² - (v * w)²

Þ     (v * w)² £ | v |²·| w |²

Þ     | v * w | £ | v |·| w |

Zu 6.:  "Þ" Für w = 0 ist wieder nichts zu zeigen; sei also w ¹ 0. Wie im Beweis zu 4. errechnen wir:

(v - cw)² = ${| v |}^{2} - 2 \frac{{(v_{*} w)}^{2}}{| w |^{2}} + \frac{{(v_{*} w)}^{2}}{| w |^{2}}$

= ${| v |}^{2} - 2 \frac{{| v |}^{2} {| w |}^{2}}{| w |^{2}} + \frac{{| v |}^{2} {| w |}^{2}}{| w |^{2}}$

= | v |² - 2| v |² + | v |²

= 0.

Damit aber ist | v - cw | = 0, also v = cw. Die Sequenz v,w ist daher linear abhängig.
"Ü": Sei nun v,w linear abhängig, etwa v = aw. Dann rechnet man der Reihe nach:

| v * w | = | aw * w | = | a | | w * w | = | a | | w |² = | a | | w |·| w | = | aw |·| w | = | v |·| w |.

Zu 7.:  Wir betrachten wieder nur die Quadrate:

| v + w |²

= (v + w)²

= v² + 2(v * w) + w²

£ v² + 2|v * w| + w²

£ v² + 2| v |·| w | + w²        (Cauchy-Schwarz)

= | v |² + 2| v |·| w | + | w |²

= (| v | + | w |)².

Zu 8.: Die Behauptung folgt sofort aus | v | = | v - w + w | £ | v - w | + | w |.
Zu 9.: | v + w |² + | v - w |² = (v + w)² + (v - w)² = v² + 2(v * w) + w² + v² - 2(v * w) + w² = 2| v |² + 2 | w |².

Bemerkung und Bezeichnung: Es sei V ein euklidischer Vektorraum, v Î V. Ist v ¹ 0, so setzt man

$v ° : = \frac{v}{| v |}$ .

v° heißt der zu v gehörige Einheitsvektor. Dabei gilt:

| v° | = 1.

< v° > = < v >.

Beweis:

Zu 1.:   $| v ° | = | \frac{1}{| v |} v | = \frac{1}{| v |} | v | = 1$ .

Zu 2.:   Die Gleichheit folgt mit v = | v | v° aus einer elementaren Gesetzmäßigkeit für Erzeugnisse.

Direkt verbunden mit dem Längenbegriff ist das Konzept der Abstandsmessung. Die folgende Definition orientiert sich an den Verhältnissen desRⁿ. Hier repräsentiert der Vektor x - y die Nebendiagonale des von x und y aufgespannten Prallelogramms; seine Länge | x - y | mißt also die Entfernung zwischen den Punkten x und y.

Definition: Es sei V ein euklidischer Vektorraum. Für v,w Î V heißt die Zahl

| v - w |

Abstand von v zu w.

Bemerkung: In einem euklidischen Vektorraum V gilt für alle u,v,w Î V:

| v - w | = | w - v |.

| v - 0 | = | v |.

| v - w | = 0 Û v = w.

| v - w | £ | v - u | + | u - w |.

Beweis: Alle Punkte werden auf die entsprechenden Eigenschaften der Länge zurückgeführt. 2. ist offensichtlich richtig.

Zu 1.: | v - w | = | -(v - w) | = | w - v |.

Zu 3.: | v - w | = 0 Û v - w = 0 Û v = w.

Zu 4.: | v - w | = | v - u + u - w | £ | v - u | + | u - w |.

Die Existenz eines Abstandsbegriffs eröffnet für euklidische Vektorräume eine völlig neue Perspektive: Grundprinzipien der reellen Analysis lassen sich in geeigneter Weise auf euklidische Vektorräume übertragen! Dieses Konzept soll am Beispiel der Konvergenz vorgestellt werden.

Definition: Es sei V ein euklidischer Vektorraum (v_n) eine Folge in V und v Î V.

Wir sagen (v_n) konvergiert gegen v (in Zeichen: v_n ® v), falls es zu jedem e > 0 ein n₀ Î N gibt, so dass

| v_n - v | < e für alle n ³ n₀.

Falls v_n ® v, so nennen wir (v_n) konvergent und v einen Grenzwert (oder Limes) von (v_n).

(v_n) heißt Cauchy-Folge, falls es zu jedem e > 0 ein n₀ Î N gibt, so dass

| v_n - v_m | < e für alle n,m ³ n₀.

V heißt vollständig, falls jede Cauchy-Folge konvergiert.

Bemerkung: V sei ein euklidischer Vektorraum. Dann gilt:

Jede Folge (v_n) in V hat höchstens einen Grenzwert.

Jede konvegente Folge ist eine Cauchy-Folge.

v_n ® v   Ù w_n ® w   Þ    av_n + bw_n ® av + bw.

Beweis:

Zu 1.: Angenommen v und v' sind zwei verschiedene Grenzwerte von (v_n). Dann gibt es zu jedem e > 0 ein n, so dass

| v_n - v | < $\frac{ϵ}{2}$     Ù     | v_n - v' | < $\frac{ϵ}{2}$

Þ     | v - v' | = | v - v_n + v_n - v' | £ | v_n - v | + | v_n - v' | < e

Þ     | v - v' | = 0

Þ     v - v' = 0 im Widerspruch zu v ¹ v'.

Zu 2.: Sei (v_n) konvergent gegen v und e > 0 vorgegeben. Dann gibt es ein n₀, so dass | v_n - v | < $\frac{ϵ}{2}$ für alle n ³ n₀.
Damit hat man für n,m ³ n₀:

| v_n - v_m | = | v_n - v + v - v_m | £ | v_n - v | + | v_m - v | < e.

Zu 3.: Ist e > 0 vorgegeben, so gibt es n₁,n₂, so dass

| v_n - v | < $\frac{ϵ}{2 (| α | + 1)}$ für alle n ³ n₁,
| w_n - w | < $\frac{ϵ}{2 (| β | + 1)}$ für alle n ³ n₂.

Für alle n ³ n₀ := max{n₁,n₂}gilt damit:

| av_n + bw_n - (av + bw) | £ |a|| v_n - v | + |b|| w_n - w | < $\frac{| α | ϵ}{2 (| α | + 1)} + \frac{| β | ϵ}{2 (| β | + 1)}$ £ e.

Beachte:

In R^m ist der neue Konvergenzbegriff stark an den alten gekoppelt. Hier nämlich läßt sich die Konvergenz durch die koordinatenweise Konvergenz ersetzen:

x_n ® x Û (x_n)₁ ® x₁ Ù .... Ù (x_n)_m ® x_m.

Denn wegen | x_n - x |² = | (x_n)₁ - x₁ |² + .... + | (x_n)_m - x_m |² kann man folgendermaßen argumentieren:
- "Þ": Ist | x_n - x |² < e² für alle n ³ n₀, so gilt für diese n und für jedes k Î {1,...,m}:
  | (x_n)_k - x_k |² £ | x_n - x |² < e².
- "Þ": Ist | (x_n)_k - x_k |² < $\frac{ϵ^{2}}{m}$ für jedes k Î {1,...,m} und für alle n ³ n₀, so gilt für diese n:
  | x_n - x |² < e².

Auch für das zweite geometrische Grundkonzept, die Winkelmessung, lassen wir uns durch die Verhältnisse im Rⁿ motivieren. Betrachtet man etwa zwei Einheitsvektoren des R², so läßt sich der Kosinus des Winkel zwischen diesen Vektoren elementargeometrisch am Einheitskreis ermitteln.

Nach der Skizze ist a - b der Winkel zwischen x und y.
Seinen Kosinus können wir mit Hilfe des Additionstheorems
berechnen:

cos(a - b) = cos a cos b + sin a sin b

= x₁y₁ + x₂y₂

= x × y

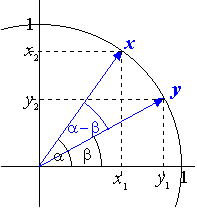Diese Beziehung kann man nun leicht auf beliebige Skalarprodukte verallgemeinern:

Definition: Ist V ein euklidischer Vektorraum, so heißt für v,w Î V, v,w ¹ 0 die Zahl

$∠ (v, w) : = {cos}^{- 1} (\frac{v_{*} w}{| v | ċ | w |})$ Î [0,p]

das Winkelmaß zwischen v und w.

Beachte:

Die Cauchy-Schwarzsche Ungleichung garantiert $| \frac{v_{*} w}{| v | ċ | w |} | \leq 1$ , somit ist die Zahl Ð(v,w) wohldefiniert.
Durch Umstellen der Definitionsgleichung für das Winkelmaß erhält man eine alternative Darstellung für das Skalarprodukt:

v * w = | v |·| w |·cos(Ð(v,w)).
Einen Winkel zwischen v und 0 definieren wir nicht.
In Rⁿ ist Ð(x, y) das Bogenmaß des von den Vektoren x und y gebildeten Winkels.

Beispiel:

in Rⁿ:
- $∠ ((\begin{matrix} 1 \\ 1 \end{matrix}), (\begin{matrix} - 2 \\ 2 \end{matrix})) = {cos}^{- 1} \frac{(\begin{matrix} 1 \\ 1 \end{matrix}) ċ (\begin{matrix} - 2 \\ 2 \end{matrix})}{| (\begin{matrix} 1 \\ 1 \end{matrix}) | ċ | (\begin{matrix} - 2 \\ 2 \end{matrix}) |} = {cos}^{- 1} (\frac{0}{\sqrt{2} ċ \sqrt{8}}) = {cos}^{- 1} (0) = \frac{π}{2}$ .
- $∠ ((\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}), (\begin{matrix} 1 \\ 1 \\ 0 \end{matrix})) = {cos}^{- 1} \frac{(\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}) ċ (\begin{matrix} 1 \\ 1 \\ 0 \end{matrix})}{| (\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}) | ċ | (\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}) |} = {cos}^{- 1} (\frac{1}{\sqrt{2} ċ \sqrt{2}}) = {cos}^{- 1} (\frac{1}{2}) = \frac{π}{3}$ .
in C ⁰([0,1]):
- $∠ (X, X^{4}) = {cos}^{- 1} (\frac{\int_{0}^{1} X^{5}}{\sqrt{\int_{0}^{1} X^{2}} \sqrt{\int_{0}^{1} X^{8}}}) = {cos}^{- 1} (\frac{\frac{1}{6}}{\sqrt{\frac{1}{3}} \sqrt{\frac{1}{9}}}) = {cos}^{- 1} (\frac{1}{2} \sqrt{3}) = \frac{π}{6}$ .

Bemerkung: Es sei V ein euklidischer Vektorraum, v,w Î V, v,w ¹ 0. Dann gilt für a ¹ 0:

Ð(v,v) = 0.

Ð(v,w) = Ð(w,v).

Ð(av,w) = Ð(v,w).

Ð(v,w) = Ð(v°,w°) = cos^-1(v° * w°).

Beweis:

Zu 1.: $∠ (v, v) = {cos}^{- 1} (\frac{v_{*} v}{| v | ċ | v |}) = {cos}^{- 1} (\frac{| v |^{2}}{| v |^{2}}) = {cos}^{- 1} (1) = 0$ .

Zu 2.: $∠ (v, w) = {cos}^{- 1} (\frac{v_{*} w}{| v | ċ | w |}) = {cos}^{- 1} (\frac{w_{*} v}{| w | ċ | v |}) = ∠ (w, v)$ .

Zu 3.: $∠ (α v, w) = {cos}^{- 1} (\frac{{α v}_{*} w}{| α v | ċ | w |}) = {cos}^{- 1} (\frac{α}{| α |} \frac{v_{*} w}{| v | ċ | w |}) = {cos}^{- 1} (\frac{α}{α} \frac{v_{*} w}{| v | ċ | w |}) = ∠ (v, w)$ .

Zu 4.: Die erste Gleichung folgt aus 3., die zweite direkt aus der Definition.

Wir ziehen nun Abbildungen zwischen euklidischen Vektorräume mit in unsere Betrachtungen ein. Diejenigen unter ihnen, die die geometrischen Zusatzeigenschaften respektieren zeichnen wir durch einen Namen aus.

Definition:   V und W seien zwei euklidische Vektorräume. Eine Funktion f : V ® W heißt

längentreu, falls   | f(v) | = | v | für alle v Î V.
abstandstreu, falls   | f(v) - f(w) | = | v - w | für alle v,w Î V.

winkeltreu, falls   v ¹ 0 Þ   f(v) ¹ 0    Ù    Ð( f(v), f(w)) = Ð(v,w) für alle v,w ¹ 0.

Beispiel:

Jede Translation T_a : V ® V , also T_a(v) = v + a, ist abstandstreu, aber (für a ¹ 0) nicht längentreu, denn:
| T_a(v) - T_a(w) | = | v + a - (w + a) | = | v - w |, und z.B. | T_a(0) | = | a | ¹ | 0 |.

Jede Streckung L_a : V ® V , also L_a(v) = av ist für a ¹ 0 winkeltreu, aber (für |a| ¹ 1) nicht längentreu, denn:
Mit v ist auch L_a(v) = av ungleich 0 und:

Ð(L_a(v),L_a(w)) = Ð(av,aw) = Ð(v,w) .

Ferner ist für |a| ¹ 1 und v ¹ 0: |L_a(v) | = | av | = | a || v | ¹ | v |.

In R² ist die Drehung (Rotation)

$R_{α} = (\begin{matrix} cos α & - sin α \\ sin α & cos α \end{matrix})$

um einen bliebigen Winkel a längen-, winkel- und abstandstreu, denn:

   ·
$\begin{array}{l} | R_{α} (x) | & = | (\begin{matrix} x_{1} cos α - x_{2} sin α \\ x_{1} sin α + x_{2} cos α \end{matrix}) | \\ = \sqrt{{(x_{1} cos α - x_{2} sin α)}^{2} + {(x_{1} sin α + x_{2} cos α)}^{2}} \\ = \sqrt{x_{1}^{2} {cos}^{2} α - 2 x_{1} x_{2} cos α sin α + x_{2}^{2} {sin}^{2} α + x_{1}^{2} {sin}^{2} α + 2 x_{1} x_{2} sin α cos α + x_{2}^{2} {cos}^{2} α} \\ = \sqrt{x_{1}^{2} {cos}^{2} α + x_{2}^{2} {sin}^{2} α + x_{1}^{2} {sin}^{2} α + x_{2}^{2} {cos}^{2} α} \\ = \sqrt{(x_{1}^{2} + x_{2}^{2}) {cos}^{2} α + (x_{2}^{2} + x_{1}^{2}) {sin}^{2} α} \\ = \sqrt{(x_{1}^{2} + x_{2}^{2}) ({cos}^{2} α + {sin}^{2} α)} \\ = \sqrt{(x_{1}^{2} + x_{2}^{2})} \\ = | x | . \end{array}$

   ·    Wegen der Längentreue hat man zunächst für ein x ¹ 0: | R_a(x) | = | x | ¹ 0 Þ  R_a(x) ¹ 0.
Ferner reicht es, wieder wegen der Längentreue, die Gleichung Ð(R_a(x),R_a(y)) = Ð(x, y) nur für Einheitsvektoren x und y zu bestätigen. Dies ergibt sich nun direkt aus folgender Rechnung:

$\begin{array}{l} R_{α} (x) ċ R_{α} (y) & = (\begin{matrix} x_{1} cos α - x_{2} sin α \\ x_{1} sin α + x_{2} cos α \end{matrix}) ċ (\begin{matrix} y_{1} cos α - y_{2} sin α \\ y_{1} sin α + y_{2} cos α \end{matrix}) \\ = x_{1} y_{1} {cos}^{2} α - x_{1} y_{2} cos α sin α - x_{2} y_{1} sin α cos α + x_{2} y_{2} {sin}^{2} α \\ &quad;&quad; + x_{1} y_{1} {sin}^{2} α + x_{1} y_{2} sin α cos α + x_{2} y_{1} cos α sin α + x_{2} y_{2} {cos}^{2} α \\ = (x_{1} y_{1} + x_{2} y_{2}) {cos}^{2} α + (x_{1} y_{1} + x_{2} y_{2}) {sin}^{2} α \\ = x_{1} y_{1} + x_{2} y_{2} \\ = x ċ y . \end{array}$

   ·    Die Abstandstreue folgt mit der nächsten Bemerkung aus der Längentreue.

Bemerkung: Es sei f : V ® W eine lineare Abbildung zwischen zwei euklidischen Vektorräumen. Dann gilt:

f ist längentreu Û f ist abstandstreu.

Beweis:

"Þ": | f(v) - f(w) | = | f(v - w) | = | v - w |.

"Ü": | f(v) | = | f(v) - f(0) | = | v - 0 | = | v |.

Die verschiedenen Treueeigenschaften sind mit der Hintereinanderausführung verträglich:

Bemerkung: U, V und W seien drei euklidische Vektorräume. f : V ® W und g : U ® V zwei Abbildungen, dann gilt:

f und g längentreu     Þ     $f \circ g$ längentreu.

f und g abstandstreu     Þ     $f \circ g$ abstandstreu.

f und g winkeltreu     Þ     $f \circ g$ winkeltreu.

Beweis: Für v,w Î U hat man:

Zu 1.: | f(g(v)) | = | g(v) | = | v |    für alle v Î U.

Zu 2.: | f(g(v)) - f(g(w)) | = | g(v) - g(w) | = | v - w |    für alle v,w Î U.

Zu 3.: Zunächst hat man für ein v ¹ 0: g(v) ¹ 0   Þ    f(g(v)) ¹ 0.
Und weiter: Ð( f(g(v)), f(g(w))) = Ð(g(v),g(w)) = Ð(v,w)    für alle v,w ¹ 0.

9.12

9.14.

- - - - - Diese Seite braucht webEQ! Klicken Sie auf das Logo. - - - - -
9.13. Skalarprodukte