9.12. Verallgemeinerte Differenzierbarkeit

Methoden der linearen Algebra mit Begriffen aus der Analysis zu kombinieren, führt oft zu reichhaltigen, neuen Theorien. In diesem Abschnitt soll eine solche Kombination am Beispiel der Differenzierbarkeit vorgestellt werden. Die resultierende neue Theorie, die Distributionentheorie, wurde gegen Ende der 1940er Jahre von Laurent Schwartz entwickelt.

Wir beschränken uns auf einige grundlegende Aspekte der Distributionentheorie, die bereits mit sparsamen Bedingungen entwickelt werden können. Die folgenden drei Punkte sind daher zu beachten:

• Unsere Distributionen müssen nur eine algebraische Bedingung, die Linearität, erfüllen. Die sonst übliche Forderung nach einem speziellen Konvergenzverhalten stellen wir nicht.
   
• Mit dem Stammfunktionen-Integral steht uns nur ein eingeschränkter Integralbegriff zur Verfügung. Das eine oder andere Beispiel wird daher nicht in der größtmöglichen Allgemeinheit dargestellt werden können.
   
• Nach wie vor betrachten wir nur reelle Funktionen in einer Veränderlichen.
   

Wir beginnen mit der Bereitstellung der für die Theorie notwendigen Grund- oder Testfunktionen. Dabei sei noch einmal an den Begriff "Träger einer Funktion" erinnert: ${\displaystyle \text{supp}g=\{x\in ℝ|g(x)\ne 0\}}$.

 
Beachte:
Eine ${\displaystyle C^{\infty }}$-Funktion ist also nur dann eine Testfunktion, wenn sie außerhalb eines geschlossenen Intervalls nur den Wert 0 annimmt. Unter den gewöhnlichen ${\displaystyle C^{\infty }}$-Funktionen findet man ein solches Verhalten eher nicht. Es müssen also Beispiele konstruiert werden.

Dabei spielt die Funktion ${\displaystyle f:ℝ\to ℝ}$ gegeben durch ${\displaystyle f(x)=\{\begin{array}{l}{e}^{-\frac{1}{x}},\text{falls}x>0\hfill \\ \mathrm{0,}\text{falls}x\le 0\hfill \end{array}}$

eine große Rolle.  f ist eine ${\displaystyle C^{\infty }}$-Funktion, denn wir zeigen für alle ${\displaystyle n\in {\mathbb{N}}^{\ast }}$:

Dem Induktionsbeweis stellen wir zunächst eine Abschätzung voran, die während der Induktion benötigt wird:
Für ${\displaystyle i\in \mathbb{N}}$ und ${\displaystyle x>0}$ erhält man aus ${\displaystyle x^i\cdot e^{\frac{1}{x}}=\sum _{n=0}^{\infty }\frac{x^i}{n!x^n}>\frac{1}{(i+1)!x}}$ die Ungleichung:
 

Nun zur Induktion selbst:

1.  Wir weisen die Differenzierbarkeit von  f  in jedem ${\displaystyle x\in ℝ}$ nach und unterscheiden dazu drei Fälle:

• ${\displaystyle x<0}$: Hier ist f lokal identisch mit 0, also differenzierbar mit Ableitung 0.
• ${\displaystyle x>0}$: Hier ist f lokal identisch mit ${\displaystyle e^{-\frac{1}{x}}}$, also differenzierbar nach Kettenregel. Mit ${\displaystyle a_1=\mathrm{0,}{a}_2=1}$ ist:
  ${\displaystyle f^{\prime }(x)=\frac{1}{x^2}{e}^{-\frac{1}{x}}=(\sum _{i=1}^2\frac{a_i}{x^i})e^{-\frac{1}{x}}}$.

• ${\displaystyle x=0}$: Hier muß die Differenzenquotientenfunktion ${\displaystyle m_0}$ berechnet werden. Aus
   
  ${\displaystyle m_0(x)=\frac{f(x)-f(0)}{x-0}=\frac{f(x)}{x}=\{\begin{array}{l}\frac{e^{-\frac{1}{x}}}{x},\text{falls}x>0\hfill \\ 0,\text{falls}x\le 0\hfill \end{array}}$
   
  erhält man mittels (+) die Abschätzung ${\displaystyle 0\le m_0(x)\le 2!|x|}$. Folgt: ${\displaystyle \underset{x\to 0}{\lim }{m}_0(x)=0}$. Also ist; f in 0 differenzierbar mit ${\displaystyle f^{\prime }(0)=0}$.

2.  Sei jetzt  f bereits n-mal differenzierbar und ${\displaystyle f^{(n)}(x)}$ wie angegeben zu berechnen. Um nun die Differenzierbarkeit von ${\displaystyle f^{(n)}}$ sicherzustellen, sind wieder die drei charakteristischen Fälle zu unterscheiden:

• ${\displaystyle x<0}$:   ${\displaystyle f^{(n)}}$ ist hier wieder lokal identisch mit 0, also differenzierbar mit Ableitung 0.
• ${\displaystyle x>0}$:   Hier ist ${\displaystyle f^{(n)}}$ lokal identisch mit ${\displaystyle (\sum _{i=1}^{2n}\frac{a_i}{{\mathrm{X}}^i})e^{-\frac{1}{\mathrm{X}}}}$, also differenzierbar nach Produkt- und Kettenregel. Die Ableitung errechnet man mit geeignet gewählten Konstanten ${\displaystyle a{\text{'}}_i}$ zu:
  ${\displaystyle \begin{array}{ll}{f}^{(n+1)}(x)=f^{(n)\text{'}}(x)\hfill & =(\sum _{i=1}^{2n}\frac{-i\cdot a_i}{x^{i+1}})e^{-\frac{1}{x}}+(\sum _{i=1}^{2n}\frac{a_i}{x^i})\frac{1}{x^2}{e}^{-\frac{1}{x}}\hfill \\ \hfill & =(\sum _{i=1}^{2n}\frac{-i\cdot a_i}{x^{i+1}})e^{-\frac{1}{x}}+(\sum _{i=1}^{2n}\frac{a_i}{x^{i+2}})e^{-\frac{1}{x}}\hfill \\ \hfill & =(\sum _{i=1}^{2(n+1)}\frac{a{\text{'}}_i}{x^i})e^{-\frac{1}{x}}.\hfill \end{array}}$

• ${\displaystyle x=0}$:   Auch hier folgt aus
  ${\displaystyle m_0(x)=\frac{f^{(n)}(x)-f^{(n)}(0)}{x-0}=\{\begin{array}{l}(\sum _{i=1}^{2n}\frac{a_i}{x^{i+1}})e^{-\frac{1}{x}}=\sum _{i=1}^{2n}{a}_i\frac{e^{-\frac{1}{x}}}{x^{i+1}},\text{falls}x>0\hfill \\ \mathrm{0,}\text{falls}x\le 0\hfill \end{array}}$
  mit (+) die Abschätzung ${\displaystyle 0\le |m_0(x)|\le \underset{≕c}{\underbrace{\sum _{i=1}^n|a_i|(i+2)!}}|x|=c|x|}$, und damit: ${\displaystyle f^{(n+1)}(0)=\underset{x\to 0}{\lim }{m}_0(x)=0}$.

Mit Hilfe dieser ${\displaystyle C^{\infty }}$-Funktion f lassen sich nun leicht Beispiele von Testfunktionen herstellen.
  

Beispiel:  Für jedes ${\displaystyle r>0}$ ist die Funktion ${\displaystyle g_r:ℝ\to ℝ}$ gegeben durch ${\displaystyle g_r=f\circ (r^2-{\mathrm{X}}^2)}$ eine Testfunktion mit ${\displaystyle \text{supp}{g}_r\subset [-r,r]}$. Beweis: Nach Kettenregel ist ${\displaystyle g_r}$ eine ${\displaystyle C^{\infty }}$-Funktion. Ihr Träger ist eine Teilmenge von ${\displaystyle [-r,r]}$, denn ist ${\displaystyle |x|>r}$, so ist ${\displaystyle r^2-x^2<0}$, also: ${\displaystyle f(r^2-x^2)=0}$.

Oft setzt man eine normierte Form der gerade konstruierten Testfunktion ${\displaystyle g_r}$ ein. Weil nämlich ${\displaystyle g_r(x)>0}$ für alle ${\displaystyle x\in [-r,r]}$,
ist ${\displaystyle \underset{-r}{\overset{r}{\int }}{g}_r\ne 0}$. Die Funktion ${\displaystyle g_r^0=\frac{1}{\underset{-r}{\overset{r}{\int }}{g}_r}{g}_r}$ ist somit eine Testfunktion mit der besonderen Eigenschaft ${\displaystyle \underset{-r}{\overset{r}{\int }}{g}_r^0=1}$.

Die folgenden Skizzen zeigen die Funktionen ${\displaystyle g_1}$ und ${\displaystyle g_1^0}$.

g1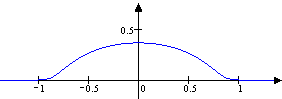

g1 0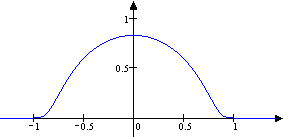

Ein weiteres Beispiel dokumentiert die hohe Flexibilität der Testfunktionen. Überdies sind die hier eingeführten Hut-Funktionen ein unentbehrliches Hilfsmittel bei der Entwicklung allgemeiner Integrale. Wir notieren zwei Varianten.
 

Beispiel: (Satz vom ${\displaystyle C^{\infty }}$-Hut) Ist ${\displaystyle 0<r<s}$, so gibt es eine Testfunktion ${\displaystyle h\in C_0^{\infty }}$ mit   ${\displaystyle 0\le h(x)\le 1}$ für alle ${\displaystyle x\in ℝ}$ ${\displaystyle h(x)=1}$ für ${\displaystyle |x|\le r}$ ${\displaystyle h(x)=0}$ für ${\displaystyle |x|\ge s}$.   Zu jedem abgeschlossenen Intervall ${\displaystyle [c,d]}$ und jedem ${\displaystyle \epsilon >0}$ gibt es eine Testfunktion ${\displaystyle h_{\epsilon }\in C_0^{\infty }}$ mit   ${\displaystyle 0\le h_{\epsilon }(x)\le 1}$ für alle ${\displaystyle x\in ℝ}$ ${\displaystyle h_{\epsilon }(x)=1}$ für ${\displaystyle x\in [c,d]}$ ${\displaystyle h_{\epsilon }(x)=0}$ für ${\displaystyle x\notin [c-\epsilon ,d+\epsilon ]}$   Jede Funktion dieser Art nennen wir einen 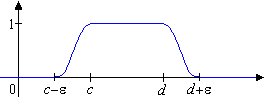${\displaystyle C^{\infty }}$-Hut für ${\displaystyle [c-\epsilon ,d+\epsilon ]}$. Beweis: Zu 1.:  Wir setzen wieder die oben eingeführte ${\displaystyle C^{\infty }}$-Funktion  f ein. Für ${\displaystyle |x|>r}$ ist ${\displaystyle f(x^2-r^2)>0}$, für ${\displaystyle |x|<s}$ ist ${\displaystyle f(s^2-x^2)>0}$. Da stets ${\displaystyle f(x)\ge 0}$, hat man für alle x:   ${\displaystyle f(x^2-r^2)+f(s^2-x^2)>0}$. Die Funktion ${\displaystyle h≔\frac{f\circ (s^2-{\mathrm{X}}^2)}{f\circ ({\mathrm{X}}^2-r^2)+f\circ (s^2-{\mathrm{X}}^2)}}$   ist daher eine ${\displaystyle C^{\infty }}$-Funktion auf ganz ${\displaystyle ℝ}$. Sie besitzt offensichtlich die drei angegebenen Eigenschaften. Zu 2.:  Wir gewinnen einen ${\displaystyle C^{\infty }}$-Hut für ${\displaystyle [c-\epsilon ,d+\epsilon ]}$ durch eine geeignete Verschiebung der gerade konstruierten Funktion h: Setzt man in 1. ${\displaystyle r=\frac{d-c}{2}}$ und ${\displaystyle s=r+\epsilon }$, so leistet die ${\displaystyle C^{\infty }}$-Funktion   ${\displaystyle h_{\epsilon }=h\circ (\mathrm{X}-\frac{c+d}{2})}$ das Gewünschte: Ist ${\displaystyle x\in [c,d]}$, so ist ${\displaystyle |x-\frac{c+d}{2}|\le r}$, d.h. ${\displaystyle h_{\epsilon }(x)=h(x-\frac{c+d}{2})=1}$. Liegt x außerhalb ${\displaystyle ]c-\epsilon ,d+\epsilon [}$, so ist ${\displaystyle |x-\frac{c+d}{2}|\ge s}$, also ist ${\displaystyle h_{\epsilon }(x)=h(x-\frac{c+d}{2})=0}$.

Beliebige Funktionen nehmen definitionsgemäß außerhalb ihres Träger nur den Wert 0 an. Bei einer ${\displaystyle C_0^{\infty }}$-Funktion g gilt dieses Verhalten in geeigneten Bereichen sogar für alle Ableitungen ${\displaystyle g^{(n)}}$! Die folgende Bemerkung führt dies präzise aus:
 

Bemerkung:  Es sei ${\displaystyle g\in C_0^{\infty }}$ und ${\displaystyle [a,b]}$ ein Intervall, das den Träger von g umfasst, also ${\displaystyle \text{supp}g\subset [a,b]}$. Dann gilt für alle ${\displaystyle n\ge 0}$: ${\displaystyle g^{(n)}(x)=0}$ für alle ${\displaystyle x<a}$. ${\displaystyle g^{(n)}(x)=0}$ für alle ${\displaystyle x>b}$.   ${\displaystyle g^{(n)}(a)=0}$. ${\displaystyle g^{(n)}(b)=0}$. Beweis: Zu 1.:  In jedem Punkt ${\displaystyle x<a}$ bzw. ${\displaystyle x>b}$ ist g lokal identisch mit 0, stimmt hier also mit dem Ableitungsverhalten der Nullfunktion überein. Zu 2.:  Als differenzierbare Funktion ist ${\displaystyle g^{(n)}}$ in a stetig. Mit ${\displaystyle g^{(n)}(0)=0}$ für alle ${\displaystyle x<a}$ ist somit auch: ${\displaystyle g^{(n)}(a)=0}$. Auf ähnliche Weise ergibt sich: ${\displaystyle g^{(n)}(b)=0}$.

Die folgende Definition vermischt nun Inhalte der Analysis mit algebraischen Aspekten.
 

Definition und Bemerkung:  ${\displaystyle C_0^{\infty }}$ ist ein Untervektorraum von ${\displaystyle C^{\infty }(ℝ)}$. Den zugehörigen Dualraum, also den Vektorraum der Linearformen auf ${\displaystyle C_0^{\infty }}$ bezeichnen wir mit dem Symbol ${\displaystyle D≔C_0^{\infty }\text{'}=\{L:C_0^{\infty }\to ℝ|L\text{ist linear}\}}$ Die Elemente von D nennen wir verallgemeinerte Funktionen oder Distributionen. Beweis:  Wir weisen für ${\displaystyle C_0^{\infty }}$ die drei kennzeichnenden Eigenschaften eines Unterraums nach: ${\displaystyle 0\in C^{\infty }(ℝ)}$ und ${\displaystyle \text{supp}0=\varnothing \subset [\mathrm{0,1}]}$.   Sind ${\displaystyle g_1,g_2\in C_0^{\infty }}$ so sind dies zwei ${\displaystyle C^{\infty }}$-Funktionen, deren Träger jeweils in einem Intervall liegen, etwa ${\displaystyle \text{supp}{g}_1\subset [a_1,b_1]}$ bzw. ${\displaystyle \text{supp}{g}_2\subset [a_2,b_2]}$. Dann ist auch ${\displaystyle g_1+g_2}$ eine ${\displaystyle C^{\infty }}$-Funktion. Für ihren Träger gilt:   ${\displaystyle \text{supp}{g}_1+g_2\subset [a_1,b_1]\cup [a_2,b_2]\subset [\min \{a_1,a_2\},\max \{b_1,b_2\}]}$.   Ist ${\displaystyle g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$ und ${\displaystyle \alpha \in ℝ}$, so ist ${\displaystyle \alpha g}$ eine ${\displaystyle C^{\infty }}$-Funktion deren Träger leer ist (falls ${\displaystyle \alpha =0}$) oder gleich ${\displaystyle \text{supp}g}$ ist (falls ${\displaystyle \alpha \ne 0}$). In jedem Fall also hat man: ${\displaystyle \text{supp}\alpha g\subset [a,b]}$.

 

Beispiel:  Die Diracsche Deltaform ${\displaystyle {\delta }_a}$ ist nach einem Beispiel in 9.10 eine Distribution.

Das nächste Beispiel stellt eine ganze Gruppe von Distributionen vor. Der Ausdruck verallgemeinerte Funktion hat hier seinen Ursprung.
  

Definition und Beispiel:  Ist ${\displaystyle f:ℝ\to ℝ}$ eine stetige Funktion, so ist durch die Festsetzung ${\displaystyle L_f(g)≔\underset{a}{\overset{b}{\int }}f\cdot g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$. eine Distribution ${\displaystyle L_f}$ gegeben. Distributionen dieser Form nennen wir regulär. Beweis:  Als stetige Funktion ist ${\displaystyle f\cdot g}$ integrierbar. Wir zeigen zunächst: Das Integral hängt von Wahl des Intervalls ${\displaystyle [a,b]}$ nicht ab, ${\displaystyle L_f(g)}$ ist also wohldefiniert. Sei dazu ${\displaystyle [a\text{'},b\text{'}]}$ ein weiteres Intervall mit ${\displaystyle \text{supp}g\subset [a\text{'},b\text{'}]}$. Setzt man ${\displaystyle a^{\ast }=\min \{a,a\text{'}\}}$ und ${\displaystyle b^{\ast }=\max \{b,b\text{'}\}}$, so ist    ${\displaystyle [a,b],[a\text{'},b\text{'}]\subset [a^{\ast },b^{\ast }]}$. Auf den (möglicherweise einpunktigen) Teilintervallen ${\displaystyle [a^{\ast },a]}$ und ${\displaystyle [b,b^{\ast }]}$ ist ${\displaystyle g=0}$, man hat also:   ${\displaystyle \underset{a^{\ast }}{\overset{b^{\ast }}{\int }}f\cdot g=\underset{a^{\ast }}{\overset{a}{\int }}f\cdot g+\underset{a}{\overset{b}{\int }}f\cdot g+\underset{b}{\overset{b^{\ast }}{\int }}f\cdot g=\underset{a}{\overset{b}{\int }}f\cdot g}$. Dieselbe Überlegung für das Intervall ${\displaystyle [a\text{'},b\text{'}]}$ führt zu     ${\displaystyle \underset{a\text{'}}{\overset{b\text{'}}{\int }}f\cdot g=\underset{a^{\ast }}{\overset{b^{\ast }}{\int }}f\cdot g=\underset{a}{\overset{b}{\int }}f\cdot g}$.   Nun zur Linearität: Sind ${\displaystyle g_1,g_2\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}{g}_1\subset [a_1,b_1]}$ bzw. ${\displaystyle \text{supp}{g}_2\subset [a_2,b_2]}$, so gilt mit ${\displaystyle a=\min \{a_1,a_2\}}$ und ${\displaystyle b=\max \{b_1,b_2\}}$:   ${\displaystyle \text{supp}{\alpha }_1{g}_1+{\alpha }_2{g}_2\subset [a_1,b_1]\cup [a_2,b_2]\subset [a,b]}$. Und da, wie gerade gezeigt, das Integral nicht von der Wahl des Intervalls abhängt, kann man zur Berechnung das Intervall ${\displaystyle [a,b]}$ heranziehen:   ${\displaystyle L_f({\alpha }_1{g}_1+{\alpha }_2{g}_2)=\underset{a}{\overset{b}{\int }}f\cdot ({\alpha }_1{g}_1+{\alpha }_2{g}_2)={\alpha }_1\underset{a}{\overset{b}{\int }}f\cdot g_1+{\alpha }_2\underset{a}{\overset{b}{\int }}f\cdot g_2={\alpha }_1{L}_f(g_1)+{\alpha }_2{L}_f(g_2)}$.

 

Beispiel:   Jede konstante Funktion ${\displaystyle c:ℝ\to ℝ}$ ist stetig, die zugehörige Distribution ${\displaystyle L_c}$ also regulär. Dabei gilt offensichtlich: ${\displaystyle L_c=c{L}_1}$. ${\displaystyle {\delta }_a}$ ist nicht regulär. Beweis: Zu a.:  Für ${\displaystyle g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$ hat man:   ${\displaystyle L_c(g)=\underset{a}{\overset{b}{\int }}cg=c\underset{a}{\overset{b}{\int }}g=c{L}_1(g)}$. Zu b.:  Angenommen, es gibt eine stetige Funktion  f, so dass ${\displaystyle L_f={\delta }_a}$. Da f auf jedem abgeschlossenen Intervall beschränkt ist, findet man ein ${\displaystyle r>0}$, so dass   ${\displaystyle \underset{a-r}{\overset{a+r}{\int }}|f|<1}$. Sei nun h ein ${\displaystyle C^{\infty }}$-Hut für ${\displaystyle [a+r,a+r]}$. Die folgende Abschätzung liefert den gewünschten Widerspruch:   ${\displaystyle 1={\delta }_a(h)=|L_f(h)|=|\underset{a-r}{\overset{a+r}{\int }}f\cdot h|\le \underset{a-r}{\overset{a+r}{\int }}|f|\cdot h\le \underset{a-r}{\overset{a+r}{\int }}|f|<1}$.

Die regulären Distributionen ${\displaystyle L_f}$ sind durch "ihr"  f eindeutig bestimmt.
 

Bemerkung:  Für zwei stetige Funktionen ${\displaystyle f,h:ℝ\to ℝ}$ gilt: ${\displaystyle L_f=L_h\Rightarrow f=h}$. Beweis: Sei ${\displaystyle a\in ℝ}$ beliebig. Es reicht nun, eine Folge ${\displaystyle (g_n)}$ in ${\displaystyle C_0^{\infty }}$ zu finden, so dass für jede stetige Funktion ${\displaystyle f:ℝ\to ℝ}$ gilt: ${\displaystyle L_f(g_n)\to f(a)}$. Dann nämlich kann man folgendermaßen argumentieren: ${\displaystyle f(a)=\lim L_f(g_n)=\lim L_h(g_n)=h(a)}$. Zur Konstruktion einer solchen Folge ${\displaystyle (g_n)}$ setzen wir die normierten Testfunktionen ${\displaystyle g_r^0}$ aus dem ersten Beispiel ein. Da Integrale verschiebungsunabhängig sind, ist auch die Funktion ${\displaystyle g_n≔g_{\frac{1}{n}}^0\circ (\mathrm{X}-a)}$ eine normierte Testfunktion: ${\displaystyle \underset{a-\frac{1}{n}}{\overset{a+\frac{1}{n}}{\int }}{g}_n=1}$. Sei nun ${\displaystyle f(x^{\ast })=\max \{f(x)|x\in [a-\frac{1}{n},a+\frac{1}{n}]\}}$ und ${\displaystyle f(x_{\ast })=\min \{f(x)|x\in [a-\frac{1}{n},a+\frac{1}{n}]\}}$   (beachte: stetige Funktionen nehmen auf abgeschlossenen Intervallen Maximum und Minimum an!). Da ${\displaystyle g_n}$ positiv ist, erhält man aus der Monotonie des Integrals die folgende Abschätzung:   ${\displaystyle f(x_{\ast })=f(x_{\ast })\underset{a-\frac{1}{n}}{\overset{a+\frac{1}{n}}{\int }}{g}_n\le \underset{a-\frac{1}{n}}{\overset{a+\frac{1}{n}}{\int }}f\cdot g_n\le f(x^{\ast })\underset{a-\frac{1}{n}}{\overset{a+\frac{1}{n}}{\int }}{g}_n=f(x^{\ast })}$. D.h. also: ${\displaystyle f(x_{\ast })\le L_f(g_n)\le f(x^{\ast })}$. Nach Zwischenwertsatz gibt es daher ein ${\displaystyle {\tilde{x}}_n}$ zwischen ${\displaystyle x_{\ast }}$ und ${\displaystyle x^{\ast }}$, so dass   ${\displaystyle L_f(g_n)=f({\tilde{x}}_n)}$. Da nun offensichtlich ${\displaystyle {\tilde{x}}_n\to a}$, folgt schließlich aus der Stetigkeit von f: ${\displaystyle L_f(g_n)=f({\tilde{x}}_n)\to f(a)}$.

Reguläre Distributionen entstehen aus einer Funktion per Integration. Unser Integral, das Stammfunktionen-Integral, ermöglicht es, diesen Vorgang für jede stetige Funktion durchführen. Mit einem leistungsstärkeren Integralbegriff ließe sich allerdings eine größere Gruppe von Funktionen, die sog. lokal-integrierbaren Funktionen, zur Bildung regulärer Distributionen heranziehen.  

Die nachfolgenden Konstruktionen haben zum Ziel, wenigstens den Indikatorfunktionen von Intervallen reguläre Distributionen zuzuordnen. Dabei werden wir zwischen einem offenen und einem abgeschlossenen Intervall keinen Unterschied machen. Die Bezeichnung ${\displaystyle (c,d)}$ stehe daher im Weiteren für irgendein Intervall, wie etwa ${\displaystyle [c,d[}$.

Analog führt man für ein festes ${\displaystyle d\in ℝ}$ die Distribution ${\displaystyle L_{{\chi }_{]-\infty ,d)}}=L_{{\chi }_{]-\infty ,d]}}=L_{{\chi }_{]-\infty ,d[}}}$ ein. Für ein beliebiges Intervall ${\displaystyle (c,d)}$ setzen wir:
 

 

Beispiel:  ${\displaystyle L_H=L_{{\chi }_{]\mathrm{0,}\infty [}}}$ ${\displaystyle L_{sign}=L_{{\chi }_{]\mathrm{0,}\infty [}}-L_{{\chi }_{]-\infty \mathrm{,0}[}}}$

Wir verallgemeinern nun den Ableitungsbegriff. Die Regel der partiellen Integration liefert dabei einen entscheidenden Hinweis:
Für eine stetig differenzierbare Funktion  f  und eine Testfunktion ${\displaystyle g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$ hat man nämlich:
 

 

Bemerkung:  ${\displaystyle L^{(n)}\in D}$. Beweis: Zunächst beachte man, dass mit g auch ${\displaystyle g^{(n)}\in C_0^{\infty }}$, ${\displaystyle L^{(n)}}$ ist also wohldefiniert. Es bleibt also nur noch die Linearität von ${\displaystyle L^{(n)}}$ nachzuweisen: ${\displaystyle \begin{array}{ll}{L}^{(n)}({\alpha }_1{g}_1+{\alpha }_2{g}_2)\hfill & ={(-1)}^{n}L({({\alpha }_1{g}_1+{\alpha }_2{g}_2)}^{(n)})\hfill \\ \hfill & ={(-1)}^{n}L({\alpha }_1{g}_1^{(n)}+{\alpha }_2{g}_2^{(n)})\hfill \\ \hfill & ={\alpha }_1{(-1)}^{n}L(g_1^{(n)})+{\alpha }_2{(-1)}^{n}L(g_2^{(n)})\hfill \\ \hfill & ={\alpha }_1{L}^{(n)}(g_1)+{\alpha }_{2}L(g_2).\hfill \end{array}}$

Die Distributionenableitung setzt in geeigneter Weise die klassische Ableitung fort, es handelt sich also um einen verallgemeinerten Ableitungsbegriff:
    

Bemerkung:  Für ${\displaystyle f\in C^n(ℝ)}$ gilt: ${\displaystyle L_f^{(n)}=L_{f^{(n)}}}$. Beweis:  Sei ${\displaystyle g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$. Zunächst gilt nach einer Bemerkung zuvor: ${\displaystyle g^{(i)}(a)=g^{(i)}(b)=0}$ für alle ${\displaystyle i\le n-1}$. Die partielle Integration kann also ohne Berücksichtigung der Randwerte ausgeführt werden: ${\displaystyle L_f^{(n)}(g)={(-1)}^n\underset{a}{\overset{b}{\int }}f\cdot g^{(n)}=\underset{a}{\overset{b}{\int }}{f}^{(n)}\cdot g=L_{f^{(n)}}(g)}$.

Im Distributionensinn können jetzt aber auch Funktionen abgeleitet werden, die im klassischen Sinn nicht differenzierbar sind! Wir zeigen dies am Beispiel der Betrags- und der Heavisidefunktion.
 

Beispiel:  ${\displaystyle L{\text{'}}_{|\mathrm{X}|}=L_{sign}}$. ${\displaystyle L{\text{'}}_H={\delta }_0}$. Beweis: Sei ${\displaystyle g\in C_0^{\infty }}$ mit ${\displaystyle \text{supp}g\subset [a,b]}$. Für ${\displaystyle b^{\ast }≔\max \left\{\mathrm{0,}b\right\}}$ und ${\displaystyle a_{\ast }≔\min \left\{a\mathrm{,0}\right\}}$ gilt zunächst: ${\displaystyle g(a_{\ast })=0=g(b^{\ast })}$, und damit: ${\displaystyle \begin{array}{ll}L{\text{'}}_{|\mathrm{X}|}(g)\hfill & =-L_{|\mathrm{X}|}(g\text{'})\hfill \\ \hfill & =-\underset{a}{\overset{b}{\int }}|\mathrm{X}|\cdot g\text{'}\hfill \\ \hfill & =-\underset{a^{\ast }}{\overset{0}{\int }}|\mathrm{X}|\cdot g\text{'}-\underset{0}{\overset{b_{\ast }}{\int }}|\mathrm{X}|\cdot g\text{'}\hfill \\ \hfill & =\underset{a^{\ast }}{\overset{0}{\int }}\mathrm{X}\cdot g\text{'}-\underset{0}{\overset{b_{\ast }}{\int }}\mathrm{X}\cdot g\text{'}\hfill \\ \hfill & =-\underset{a^{\ast }}{\overset{0}{\int }}g+\underset{0}{\overset{b_{\ast }}{\int }}g=L_{sign}(g).\hfill \end{array}}$ und ${\displaystyle \begin{array}{ll}L{\text{'}}_H(g)\hfill & =-L_H(g\text{'})\hfill \\ \hfill & =-\underset{0}{\overset{b_{\ast }}{\int }}g\text{'}\hfill \\ \hfill & =-(g(b_{\ast })-g(0))\hfill \\ \hfill & g(0)={\delta }_0(g).\hfill \end{array}}$

Von den klassischen Ableitungsregeln lassen sich die Summen- und die Faktorregel bequem übertragen. Die anderen Regeln stehen überhaupt nicht zur Diskussion, denn für Distributionen sind weitere Rechenarten nicht definiert.
 

Bemerkung:  Für ${\displaystyle K,L\in D}$ gilt: ${\displaystyle (K+L)\text{'}=K\text{'}+L\text{'}}$. ${\displaystyle (K-L)\text{'}=K\text{'}-L\text{'}}$. ${\displaystyle (\alpha K)\text{'}=\alpha K\text{'}}$. Beweis: Sei ${\displaystyle g\in C_0^{\infty }}$ beliebig. Zu 1.: ${\displaystyle (K+L)\text{'}(g)=-(K+L)(g\text{'})=-K(g\text{'})-L(g\text{'})=K\text{'}(g)+L\text{'}(g)}$.  2. zeigt man analog. Zu 3.: ${\displaystyle (\alpha K)\text{'}(g)=-(\alpha K)(g\text{'})=-\alpha K(g\text{'})=\alpha (-K(g\text{'}))=\alpha K\text{'}(g)}$.

9.11

9.13.