8.4. Flächenmessung
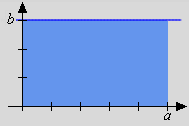
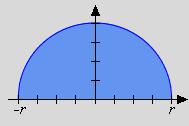
Gelegentlich lassen Integrale eine interessante geometrische Interpretation zu. Die folgenden drei Beispiele zeigen jeweils auch eine Skizze des Integranden.
-
Für ist
|
|
-
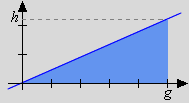
Für ist
|
|
|
|
Die errechneten Integrale stimmen in allen drei Fällen (Rechteck, Dreieck, Halbkreis) mit Flächenmaßzahlen überein, die aus der Elementargeometrie bekannt sind. Die von der x-Achse begrenzten Flächen, so zeigen es die Skizzen, liegen dabei unterhalb des Integranden f, sie werden gewissermaßen von der "Randfunktion" f im Integrationsintervall erzeugt.
Diese Übereinstimmung zwischen Flächenmaßzahlen und Integralen weckt die Hoffnung, mit Hilfe der Integrale auch weitere, krummlinig begrenzte Flächen berechnen zu können, also auch solche, zu denen die Elementargeometrie keine Formeln liefert! Die folgende Überlegung unterstützt diesen Gedanken.
Sei dazu eine positive, integrierbare Funktion. Für ein beliebiges unterteilen wir zunächst das Integrationsintervall in n viele Teilintervalle (und benennen dabei zweckmäßigerweise die Eckpunkte a und b um):
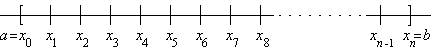
Da Integrale beliebig aufgesplittet werden können, erhält man unter Anwendung des Mittelwertsatzes [8.2.8] die folgende Berechnungsmöglichkeit:
[1]
Jeder der dabei auftretenden Summanden ist ein Produkt, und zwar aus der Länge des jeweiligen Teilintervalls und einem geeigneten Funktionswert von f. Da f positiv ist, können wir dieses Produkt als Maß eines Rechteckstreifens deuten, das Integral selbst damit also als eine Summe von Rechteckmaßen.
Die folgende Skizze zeigt die Funktion und die von ihr in erzeugte Fläche. Sie läßt sich mit dem Schieber durch die Vereinigung von Rechtecken approximieren. Die Rechteckshöhen sind dabei gemäß [1] eingestellt, so dass die Summe der Rechtecksmaße stets den Wert
13,8
i  |
|
|
hat, also den Wert des Integrals über f.
Beachte:
-
Die Reihe in [1] ist konstant, also trivialerweise konvergent gegen
. [2]
In diesem Zusammenhang erklären sich die von Leibniz eingeführten Symbole und dx: Bei der Bildung des Grenzwerts schrumpfen die Teilintervalle auf einen Punkt x zusammen, d.h. die Differenz geht in die infinitesimale Differenz dx über, für die Wahl von steht nur noch eine Möglichkeit, x, offen und das Summenzeichen mutiert zu , einem stilisierten, lang gezogenen S. Der Grenzwert [2] wird daher symbolisch notiert als
Für positive Funktionen dürfen wir das Integral also auch als Flächenmaßzahl deuten. Im Allgemeinen ist dies allerdings unzulässig, denn Flächenmaßzahlen sind stets positiv, Integrale hingegen nicht immer.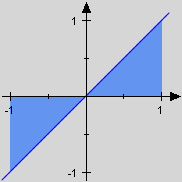 So hat etwa die Fläche, die die Identität X im Bereich mit der x-Achse erzeugt, das Maß 1. Sie ist also nicht durch das Integral gegeben. Ein bloßes Integral ist daher nur in geeigneten Fällen auch eine Flächenmaßzahl. Wie aber soll man beliebige Funktionen, also auch solche mit negativen Werten, bemessen? So hat etwa die Fläche, die die Identität X im Bereich mit der x-Achse erzeugt, das Maß 1. Sie ist also nicht durch das Integral gegeben. Ein bloßes Integral ist daher nur in geeigneten Fällen auch eine Flächenmaßzahl. Wie aber soll man beliebige Funktionen, also auch solche mit negativen Werten, bemessen?
Da das Spiegeln an der x-Achse "flächentreu" ist, müsste man nur diejenigen Graphenteile von f, die unterhalb der x-Achse liegen nach oben klappen und die anderen dort lassen, wo sie sind. Dies ist aber genau der Übergang von f zu .
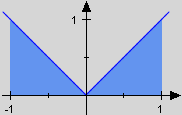 So wird denn auch die durch X gegebene Fläche exakt durch das Integral berechnet. So wird denn auch die durch X gegebene Fläche exakt durch das Integral berechnet.
In der folgenden Definition beschränken wir uns auf stetige Funktionen f. Das hat einerseits den Vorteil, dass die Integrierbarkeit von außer Frage steht, andererseits entspricht dies den anschaulichen Erwartungen, die man an den Rand einer Fläche stellt.
|
Definition: Ist f eine stetige Funktion auf , also , so nennen wir die Zahl
|
[8.4.1] |
die Maßzahl der von f im Bereich [a,b] mit der x-Achse erzeugten Fläche.
|
Bei der Ermittlung von Flächenmaßzahlen werden also nicht Stammfunktionen zu f, sondern Stammfunktionen zu benötigt. Diese zusätzliche Schwierigkeit läßt sich jedoch bei stetigen Funktionen mit endlich vielen Nullstellen elegant durch das folgende 3-Schritt-Verfahren umgehen:
-
Man errechnet in alle Nullstellen von f, und ordnet sie zusammen mit und an: .
-
Man errechnet alle Integrale der Form .
-
Als stetige Funktion hat f in allen Intervallen der Form ein einheitliches Vorzeichen. Hier läßt sich also die Integral- und die Betragsbildung vertauschen (siehe [8.2.12])! Die Flächenmaßzahl ergibt sich daher durch das betragsmäßige Aufsummieren der berechneten Integrale:
|
Beispiel:
-
Wir berechnen die Maßzahl der Fläche, die im Bereich mit der x-Achse erzeugt:
-
. Die Zerlegung erfordert also die Berechnung dreier Integrale, nämlich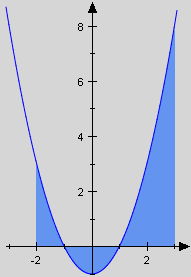
-
-
Die Flächenmaßzahl errechnet sich also zu .
-
Wir berechnen als nächstes die Maßzahl der Fläche, die im Bereich mit der x-Achse erzeugt.
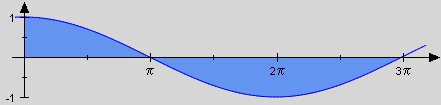
-
Da , hat man die ungeraden Vielfachen von π im Intervall zu suchen. Dies führt zur Zerlegung , so dass jetzt nur zwei Integrale zu berechnen sind.
-
und
-
Damit ergibt sich das Flächenmaß zu .
|
Alle bisher berechneten Flächen werden u.a. von der x-Achse begrenzt, haben also zumindest eine gerade Kante.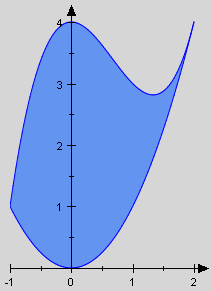 Durch einen einfachen Trick aber kommt man mit den bisherigen Methoden auch bei ausschließlich krummlinig begrenzten Flächen zurecht. Dies wird im folgenden Beispiel deutlich. Durch einen einfachen Trick aber kommt man mit den bisherigen Methoden auch bei ausschließlich krummlinig begrenzten Flächen zurecht. Dies wird im folgenden Beispiel deutlich.
Die links skizzierte Fläche läßt sich durch zwei positive Funktionen gewinnen, durch die obere Funktion

i 
|
|
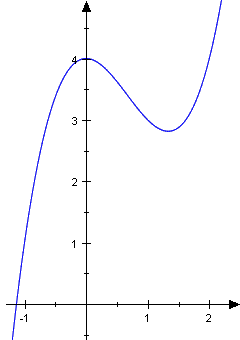
|
und die untere .

i  |
|
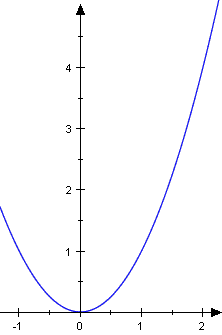
|
Dabei ist die durch f im Bereich erzeugte Fläche offensichtlich zu groß, und zwar exakt um die Fläche, die g im Bereich erzeugt. Als eine Maßzahl bietet sich daher die Differenz der beiden Flächenmaßzahlen an:
In unserer Skizze besteht kein Zweifel, welche der beiden Funktionen die obere, welche die untere ist. Im Allgemeinen aber werden die Verhältnisse nicht so übersichtlich sein und bei Funktionen mit mehr als zwei Schnittstellen gibt es solche eindeutigen Positionen überhaupt nicht! Wie aber bereits bei den zu Anfang eingeführten Flächenmaßzahlen lassen sich Probleme dieser Art mit Hilfe des Betrags elegant lösen. Wir setzen daher fest:
|
Definition: Für je zwei Funktionen nennen wir die Zahl
|
[8.4.2] |
die Maßzahl der von f und g im Bereich [a,b] erzeugten Fläche.
|
Beachte:
-
In der Regel werden zwei Funktionen vorliegen, die eine kleinste und eine größte Schittstelle, etwa a und b, besitzen. In diesem Fall nennen wir auch kurz die Maßzahl der von f und g erzeugten Fläche.
-
Bei der Berechnung von ist die Lage der x-Achse ohne Bedeutung. Liegen nämlich Teile der von f und g erzeugten Fläche unterhalb der x-Achse, so wird man durch Verschieben in der Senkrechten, etwa um c Einheiten, eine Fläche erhalten, die ganz oberhalb der x-Achse liegt. Für ihr Maß aber gilt:
-
Die Maßzahl der von f und g im Bereich [a,b] erzeugten Fläche ist per Definition die Maßzahl der von im Bereich [a,b] erzeugten Fläche. Zur Berechnung kann man daher das alte 3-Schritt-Verfahren anwenden.
So können wir etwa die Fläche aus dem Eingangsbeispiel, also die von und erzeugte Fläche, bemessen indem wir die Maßzahl der von
erzeugten Fläche ausrechen:
-
f und g besitzen nur zwei Schnittstellen, so dass lediglich ein Integral errechnet werden muss.
-
-
Die von f und g erzeugte Fläche hat also das Maß .
Die Fläche, die eine positive Funktion im Bereich [a,b] mit der x-Achse erzeugt, ist die Menge
und für jedes ist der positive Funktionswert gleichzeitig die Länge des Intervalls . Wir fassen ein solches Intervall als Schnitt
in der Menge M auf und gewinnen so das zweidimensionale Flächenmaß von M, also die Zahl , durch Integration über die eindimensionalen Maße ihrer Schnitte . Im nächsten Abschnitt wird dieser Aspekt der Flächenmessung zu einer rekursiven Möglichkeit führen, mehrdimensionale Volumina zu berechnen.
|


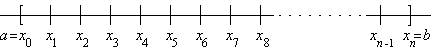
 So hat etwa die Fläche, die die Identität X im Bereich mit der
So hat etwa die Fläche, die die Identität X im Bereich mit der  So wird denn auch die durch X gegebene Fläche exakt durch das Integral berechnet.
So wird denn auch die durch X gegebene Fläche exakt durch das Integral berechnet.

 Durch einen einfachen Trick aber kommt man mit den bisherigen Methoden auch bei ausschließlich krummlinig begrenzten Flächen zurecht. Dies wird im folgenden Beispiel deutlich.
Durch einen einfachen Trick aber kommt man mit den bisherigen Methoden auch bei ausschließlich krummlinig begrenzten Flächen zurecht. Dies wird im folgenden Beispiel deutlich.
