8.10. Das Faltungsprodukt
In diesem Abschnitt nutzen wir das Integral zur Konstruktion einer interessanten und für die Analysis hilfreichen Verrechnungsart von (stetigen) Funktionen, das sogenannte Faltungsprodukt.
Mit Hilfe des Faltungsprodukts finden wir am Ende dieses Abschnitts einen günstigen, zu [7.9.16] alternativen Zugang zur Taylorformel. Auch der nachfolgende Abschnitt über Differentialgleichungen profitiert von diesem Produkt.
Im Folgenden notieren wir die Hintereinanderausführung meist in ihrer abgekürzten Form, wir schreiben also z.B. statt . Ferner beachte man, dass die in diesem Abschnitt betrachteten differenzierbaren Funktionen stets stetig differenzierbar, also Funktionen aus

i   |
|
Mit dem Symbol haben wir in [7.8.1] die Menge aller n-mal stetig differenzierbaren Funktionen bezeichnet. Dies sind n-mal differenzierbare Funktionen, deren n-te Ableitung stetig ist. Siehe dazu auch [7.8.9].
|
sind.
|
Definition: Sind f und g zwei stetige Funktionen auf , also , so heißt die Funktion
gegeben durch
|
[8.10.1] |
das Faltungsprodukt von f und g.
Man beachte, dass das angegebene Integral gemäß [8.1.5] wohldefiniert ist, denn der Integrand ist nach Voraussetzung stetig (siehe dazu [6.3.8,10]).
|
Die folgenden Beispiele erläutern den neuen Begriff. Dabei beachte man, dass das Argument x im Integranden stets als eine Konstante auftritt. Ferner wird man oft, bedingt durch die Gestalt des Integranden, auf die partielle Integration [8.3.1] zurückgreifen müssen.
|
Beispiel:
-
, denn für alle x ist
-
, denn für ein beliebiges x hat man:
-
, denn für alle x errechnen wir mittels partieller Integration:
|
In der folgenden Bemerkung stellen wir nun die elementaren Rechenregeln für das Faltungsprodukt zusammen.
|
Bemerkung: Für alle und ist
|
1.
|
[8.10.2] |
|
2.
|
[8.10.3] |
|
3.
|
[8.10.4] |
|
4.
|
[8.10.5] |
|
5.
|
[8.10.6] |
Beweis:
1. ► .
2. ► Für ein beliebiges x ist .
3. ► Wir wenden die Substitutionsregel [8.3.5] von rechts nach links an. Für ein festes x ergibt sich dann mit (beachte dabei: )
.
4. ► Für jedes x ist
.
5. ► Die Komposition ist bezüglich + rechtsdistributiv. Für ein beliebiges x hat man daher
|
Beachte:
-
Mit [8.10.4] wissen wir, dass das Faltungsprodukt kommutativ ist. Das Distributivgesetz in [8.10.6] gilt daher auch in der Form .
-
Das Distributivgesetz läßt sich auf die Subtraktion, die Multiplikation und die Division übertragen, denn verhält sich auch zu diesen Operationen rechtsdistributiv. In diesem Zusammenhang vereinbaren wir zur Einsparung von Klammern, dass stärker bindet als die Grundrechenarten.
-
[8.10.5,6] fasst man zusammen zu: "Das Faltungsprodukt ist linear in der ersten Koordinate". Mit der Kommutativität gilt dies natürlich auch für die zweite, ist also bilinear.
Wir wenden uns nun den analytischen Qualitäten des Faltungsprodukts zu. Vorab betrachten wir den reduzierten Fall . Punkt 1. der folgenden Bemerkung ist eine andere Fassung des Hauptsatzes [8.2.13]!
|
Bemerkung:
|
1. und
|
[8.10.7] |
|
2. für alle
|
[8.10.8] |
Beweis:
1. ► Zunächst hat man für jedes x: . Gemäß [8.2.13] ist daher eine Stammfunktion zu g. Insbesondere also ist differenzierbar, und mit der stetigen Ableitung g auch stetig differenzierbar.
2. ► Nach der gerade geführten Rechnung ist .
|
Wir lösen uns nun vom Spezialfall und verallgemeinern zunächst die Ableitungsregel [8.10.7].
|
Bemerkung: Sei und . Dann gilt:
|
1.
und
|
[8.10.9] |
|
2. für alle
und
|
[8.10.10] |
Beweis:
1. ►
2. ► Wir führen einen Induktionsbeweis. Da der Induktionsanfang mit 1. bereits sichergestellt ist, reicht es hier, den Induktionsschluss zu ziehen. Sei also [8.10.10] für ein beliebiges n bereits gültig.
Ist jetzt ein - also und - gegeben, mit für , so gilt nach Induktionsvoraussetzung (beachte: )
und .
Gemäß 1. ist stetig differenzierbar, also . Insgesamt ist daher und die ()-te Ableitung errechnen wir, ebenfalls mit 1., zu
.
|
Wir wenden uns nun der Ableitungsregel [8.10.8] zu. In ihrer Erweiterung auf ein beliebiges f sehen wir ein Äquivalent zur partiellen Integration [8.3.1].
|
Bemerkung: Für hat man
|
[8.10.11] |
Beweis: Wir zeigen, dass die beiden Funktionen in jedem Punkt übereinstimmen. Wegen [8.10.2] ist dabei für nichts zu zeigen. Ist , so können wir partiell integrieren:
.
|
Mit [8.10.11] können wir nun den im Eingangstext angekündigten alternativen Zugang zur Taylorformel [7.9.16] realisieren. In dieser Version der Taylorformel berücksichtigen wir nur -Funktionen auf ganz und notieren sie zunächst nur für den Entwicklungspunkt 0.
|
Bemerkung (Satz von Taylor): Sei . Jede Funktion erfüllt die Taylorformel
|
[8.10.12] |
Beweis: Es reicht offensichtlich, für alle die Folgerung
[1]
nachzuweisen. Wir führen dazu einen Induktionsbeweis:
-
Ist , so hat man für eine -Funktion f die Gleichung nachzuweisen. Dies ist aber mit [8.10.8] bereits erledigt.
-
Sei nun die Aussage [1] für ein n bereits gültig. Dann gilt für ein beliebiges mit [8.10.11] und der Induktionsvoraussetzung:
|
Beachte:
-
Durch eine Verschiebung finden wir auch eine Formulierung der Taylorformel für einen beliebigen Entwicklungspunkt a. Denn mit ergibt sich aus [8.10.12] für eine -Funktion f zunächst
,
und damit: .
Über die Rechnung (wir setzen dabei die Substitutionsregel [8.3.5] von rechts nach links ein)
erhält man daher für jedes :

i   |
|
Man ist versucht, über die Festsetzung
ein Faltungsprodukt mit Entwicklungspunkt a einführen, um dann die Taylorformel [8.10.12] in der eleganten Form
notieren zu können. Wir widerstehen dieser Versuchung.
|
|
[8.10.13] |
-
Im Spezialfall stellt die Taylorformel [8.10.13] den Mittelwertsatz [7.9.5] dar, denn nach seiner Integralversion [8.2.8] gilt für ein geeignetes zwischen a und x
Im Kontext von [8.10.13] nennt man das Polynom
das n-te Taylorpolynom und die Funktion , gegeben durch
das n-te Restglied von f bzgl. a. Man beachte auch die alternative Einführung der Taylorpolynome in 7.9. Dort wird das Restglied in seiner Lagrangeschen Form notiert.
Bei einer -Funktion gibt zu jedem n ein Restglied , so dass jetzt die Gleichung
|
[8.10.14] |
für jedes n gültig ist. Daher sind etwa diejenigen -Funktionen interessant, bei denen die Folge punktweise gegen 0 konvergiert. Denn dann ist die Taylorreihe eine konvergente Potenzreihe mit Konvergenzbereich (siehe [5.11.2]) und ihre Grenzfunktion
die Potenzreihenentwicklung oder, wie man hier auch sagt, die Taylorentwicklung von f in a. Gemäß [5.12.3] ist f damit eine analytische Funktion.
Aus dieser Beobachtung entwickeln wir nun ein Kriterium für die Analytizität einer -Funktion. Man beachte, dass nach einem Kommentar zu [7.8.10] nicht jede -Funktion analytisch ist.
|
Bemerkung (Analytizitätskriterium): Sei f eine -Funktion auf . Gibt es zu jedem eine -Umgebung und ein , so dass für alle und alle die Abschätzung
|
[8.10.15] |
gültig ist, so ist die Taylorreihe von f in a eine konvergente Potenzreihe. Auf ihrem Konvergenzbereich , , stellt sie die Taylorentwicklung von f in a dar:
für alle .
|
[8.10.16] |
f ist daher eine analytische Funktion.
Beweis: Sei beliebig und gemäß Voraussetzung gewählt. Für zeigen wir nun:
für alle . [2]
Die Darstellung [8.10.14] weist damit die Taylorreihe von f in a als eine konvergente Potenzreihe mit einem Konvergenzradius aus, deren Grenzfunktion auf mit f übereinstimmt. f ist somit analytisch und stimmt nach dem Identitätssatz [5.12.13] auch auf mit der (ebenfalls analytischen) Grenzfunktion überein.
Für ist in [2] nichts zu zeigen.
Liegt x links ( ) von a, also, so erhalten wir mit [8.2.11] und [8.2.10] die folgende Abschätzung: ) von a, also, so erhalten wir mit [8.2.11] und [8.2.10] die folgende Abschätzung:
Für alle hat man daher:
Gemäß Schachtelsatz [5.5.8] bedeutet dies: . Mit [5.5.6] ist daher [2] bewiesen.
|
Interessanterweise lässt sich auch die Umkehrung von [8.10.15] beweisen, so dass dieses Kriterium eine vollständige Charakterisierung der analytischen Funktionen auf darstellt!
|
Bemerkung: Ist analytisch, so gibt es zu jedem eine -Umgebung und ein so dass
für alle und alle
|
[8.10.17] |
Beweis: Ist f analytisch, so gibt es nach [5.12.1] eine konvergente Potenzreihe und ein , so dass
für alle . Da Potenzreihen summandenweise differenziert werden (siehe [7.5.7]), können wir die Ableitungsregel [7.8.14] einsetzen und erhalten so für diese y:
.
Nach [5.0.6] ist für alle i und alle n. Mit können wir daher für alle folgendermaßen abschätzen:
Mit

i   |
|
Man beachte dabei, dass die Potenzreihe nach [5.11.9] in absolut konvergiert.
|
, also , und ist damit Abschätzung [8.10.17] gewährleistet.
|
Beachte:
-
[8.10.15] ist sicher gewährleistet, wenn f für jedes die schärfere Bedingung
für alle
|
[8.10.18] |
erfüllt. Gelegentlich liegen sogar Funktionen mit (einheitlich) beschränkten Ableitungen vor, wie etwa sin und cos. [8.10.18] ist dann trivialerweise für alle gegeben.
-
Alle Ergebnisse lassen sich auch für ein beliebiges offenes Intervall formulieren und beweisen. Zwei der folgenden Beispiele machen davon Gebrauch.
|
Beispiel:
-
Für jedes ist die Exponentialfunktion ist analytisch. Jede ihrer Taylorreihen konvergiert auf ganz :
für alle .
|
[8.10.19] |
Beweis: Sei beliebig.
Für ist nichts zu zeigen, denn ist hier die konstante Funktion 1. Sei daher im Folgenden .
Als stetige Funktion ist auf dem abgeschlossenen Intervall beschränkt (siehe [6.6.4]). Es gibt also ein k, o.E. , so dass für alle . Mit [8.9.15] hat man daher für diese y und alle :
.
Nach [8.10.18,15] ist somit analytisch.
Die Darstellung [8.10.19] erhalten wir, wenn sich der Konvergenzradius r der Taylorreihe zu ausrechnen läßt. Mit der Konvergenz
ergibt sich dies aber direkt aus dem Quotientenkriterium [5.11.6].
► |
Für verkürzt sich [8.10.19] zu:
für alle .
|
► |
Mit erhält man daher für die e-Funktion die Taylordarstellung
,
also die ursprünglich in [5.9.18] gewählte Definition.
|
-
Für jedes ist die Potenzfunktion analytisch. Ist , so gilt für alle :

i   |
|
Man beachte die Konvention , falls .
|
|
[8.10.20] |
Beweis: Wir erinnern zunächst an die Ableitungen der Potenzfunktion (siehe [8.9.11]):
.
Sei jetzt beliebig und so gewählt, dass . Die stetige Funktion ist auf dem abgeschlossenen Intervall beschränkt. Es gibt also ein k, o.E. , so dass für alle . Da für die Funktion im Positiven monoton wächst, erhalten wir daraus:
für alle .
Mit der für gültigen Abschätzung
können wir daher für diese y folgendermaßen abschätzen:
Mit ist daher die Bedingung [8.10.15] erfüllt, also analytisch. Wir ermitteln abschließend den Konvergenzradius r der Taylorreihe
.
Gemäß [8.10.16] ist [8.10.20] gewährleistet, wenn ausfällt. Ist , so ist die Taylorreihe eine endliche Summe, denn bei fast allen Summanden tritt der Faktor auf, also ist . Im anderen Fall setzen wir das Quotientenkriterium [5.11.7] ein:
Also ist .
► |
Für etwa erhält man aus [8.10.20] die folgende Berechnungsmöglichkeit für die n-te Wurzel:
für alle
|
-
Der Logarithmus ist analytisch. Für jedes gilt:
für alle .
|
[8.10.21] |
Beweis: Per Induktion zeigt man leicht

i   |
|
Der Induktionsanfang
steht bereits in Abschnitt 8.7. Ist die Ableitungsformel für ein bereits gültig, so ist
|
:
für alle .
Sei nun beliebig und so gewählt, dass . Dann gilt mit für alle und :
.
[8.10.15] ist also erfüllt und die Taylorreihe
damit konvergent. Ihren Konvergenzradius r errechnen wir wieder mit [5.11.7] zu
,
so dass schließlich [8.10.21] bewiesen ist.
► |
Für etwa bedeutet dies:
für alle .
|
|
|
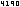 |
|
