5.12. Analytische Funktionen
Die Funktionswerte der Grenzfunktionen konvergenter Potenzreihen sind leicht zu approximieren. Es werden ja nur Addition und Multiplikation benötigt. Allein von daher ist es wünschenswert, möglichst viele Funktionen als Grenzfunktionen nachzuweisen.
Da deren Definitionsbereich aber stets ein Intervall ist, sind viele elementare Funktionen, wie etwa die Kehrwertfunktion, bereits von vornherein ausgeschlossen.
Für einen einzelnen Funktionswert reicht es aber, wenn eine Funktion lediglich lokal mit einer Grenzfunktion übereinstimmt. Mit der folgenden Definition lassen sich daher deutlich mehr Funktionen ansprechen.
|
Definition: Es sei eine nicht-leere Teilmenge von . Eine Funktion heißt analytisch, wenn es zu jedem eine konvergente Potenzreihe mit Konvergenzradius r und ein s mit gibt, so dass
|
[5.12.1] |
Die Menge aller analytischen Funktionen auf A bezeichnen wir mit dem Symbol .
|
Beachte:
Die Aufgabe, eine Funktion f als analytisch nachweisen, d.h. zu jedem a eine Darstellung gemäß [5.12.1] zu finden, formulieren wir meist so: "Man entwickle f in jedem Punkt von A in eine Potenzreihe".
Mit unseren gegenwärtigen Mitteln ist dies oft eine schwierige Aufgabe. In der Differentialrechnung werden uns allerdings weitere Techniken zur Verfügung stehen.
In einem isolierten Punkt , einem Punkt also, derart dass
für ein geeignetes , ist jedes f entwickelbar, und zwar durch jede konvergente Potenzreihe mit . [5.12.1] ist also in diesem Fall keine spezielle Eigenschaft der Funktion f.
Ist analytisch und nicht-leer, so ist auch die Einschränkung analytisch.
|
Beispiel:
|
|
[5.12.2] |
|
Denn ist vorgegeben, so gilt für jedes x mit , also mit
(man beachte den Grenzwert der geometrische Reihe [5.9.4]):
|
-
Jede Grenzfunktion einer konvergenten Potenzreihe ist nach [5.11.20] analytisch.
|
[5.12.3] |
-
Insbesondere sind damit alle Polynome sowie die Funktionen sin, cos und exp analytische Funktionen, und mit [5.12.8] dann auch tan, cot und alle Polynomquotienten.
|
[5.12.4] |
|
Analytische Funktionen verhalten sich lokal wie die Grenzfunktionen konvergenter Potenzreihen. Es ist also zu erwarten, dass deren Eigenschaften bei den analytischen Funktionen wieder auftreten. So sorgen etwa die Rechenregeln für konvergente Potenzreihen dafür, dass der Analytizitätsbegriff mit den vier Grundrechenarten verträglich ist.
|
Bemerkung: Sind f und g analytische Funktionen auf A, also: , so ist auch
-
|
[5.12.5] |
-
|
[5.12.6] |
-
|
[5.12.7] |
-
|
[5.12.8] |
Beweis: Die Nachweise zu 1. bis 4. sind nahezu identisch. Wir zeigen etwa
|
1. ►
|
Zu beliebigem gibt es und geeignete Potenzreihen mit Konvergenzradien , so dass
Für folgt dann aus [5.11.16]:
|
| Und beachten zusätzlich bei |
|
4. ►
|
Ist , so ist . Die Voraussetzung in [5.11.19] ist also gegeben.
|
|
Beachte:
Der Funktionenraum besitzt jetzt also eine algebraische Struktur: Da die konstante Funktion analytisch ist, kann man [5.12.5] und [5.12.6] zusammenfassen zu:
ist eine
ablesche Gruppe
i  |
-
Die Addition + ist assoziativ und kommutativ.
-
0 ist das neutrale Element, d.h. für alle f.
-
Jedes f besitzt genau ein inverses Element, hier , so dass ist.
|
.
Mit [5.12.7] erhält man sogar ( ist ebenfalls analytisch):
ist ein
kommutativer Ring mit Einselement
i  |
-
Es gelten die Axiome einer abelschen Gruppe.
-
Die Multiplikation · ist assoziativ und kommutativ.
-
· ist distributiv bzgl. +.
-
1 ist das neutrale Element der Multiplikation, d.h. für alle f.
|
.
Im Zusammenhang mit [5.12.8] steht eine interessante Eigenschaft analytischer Funktionen: Ist verschieden von Null, so überträgt sich dieses Verhalten auf eine ganze Umgebung von a.
|
Bemerkung: Ist analytisch und , so gibt es ein , so dass
|
[5.12.9] |
Beweis:
sei eine Potenzreihenentwicklung von f in a. Ist , also , so gibt es nach einem Argument im Beweis zu [5.11.19] ein , o.E. , so dass
.
|
Auch ein anderes Ergebnis, der Identitätssatz für konvergente Potenzreihen [5.11.14], läßt sich in geeigneter Weise auf analytische Funktionen übertragen:
|
Bemerkung: sei eine analytische Funktion und eine Folge in A mit . Sind alle Nullstellen von f, so gibt es ein , derart dass:
|
[5.12.10] |
Beweis: Wir entwickeln zunächst f in a in eine Potenzreihe, d.h. für ein geeignetes s haben wir:
.
Da , dürfen wir o.E. als eine Folge in auffassen. Nach [5.11.14] sind dann alle Koeffizienten , also ist für alle .
|
Für analytische Funktionen auf einem
Intervall
i  |
|
Wir unterscheiden hier nicht zwischen offenen und geschlossenen Intervallen. Im offenen Fall erlauben wir auch den Wert für die rechte, bzw. für die linke Ecke. und z.B. sind in diesem Sinn also auch Intervalle.
|
kann man [5.12.10] deutlich schärfer formulieren:
|
Bemerkung (Identitätssatz für analytische Funktionen): sei eine analytische Funktion auf einem Intervall, und eine Folge in I mit . Sind alle Nullstellen von f, so gilt:
|
[5.12.11] |
Beweis: Es reicht sicherlich, wenn wir für jedes zeigen:
-
-
Wir zeigen nur 1., denn der Nachweis zu 2. verläuft völlig analog. Da I ein Intervall ist, hat man zunächst . Ferner beachte man, dass ebenfalls analytisch ist.
Die beschränkte Menge
ist nicht-leer, denn nach [5.12.10] gibt es ein , o.E. , so dass . Sie besitzt daher ein Supremum .
Für jedes ist . Ist nämlich , also x keine obere Schranke von C, so gibt es in C ein . Mit ist dann auch .
Da kann man nun eine Folge in wählen, so dass . Wir wenden noch einmal [5.12.10] an und finden ein derart dass
Daraus folgt zunächst und dann , denn anderenfalls gäbe es ein x mit , so dass , also ein , das größer als das Supremum von C ist.
|
Beachte:
[5.12.11] ist nur für Intervalle gültig. Die Funktion etwa, gegeben durch
ist analytisch, aber nicht konstant 0.
Die Voraussetzung in [5.12.11] ist sicherlich gegeben, wenn es ein Teilintervall J gibt, so dass . Die folgende Version von [5.12.11] ist angenehmer zu lesen:
Ist und ein Teilintervall von I, dann gilt:
|
[5.12.12] |
Der Ring ist sogar
nullteilerfrei
i  |
|
|
, ein Integritätsring also:
Sei dazu , so dass . Ist
für ein , so ist nach [5.12.10] für alle x aus einem Teilintervall . Auf diesem Teilintervall muss daher g verschwinden: . Folgt also: .
Mit dem üblichen Differenztrick läßt sich [5.12.12] auch zum Vergleich von zwei analytischen Funktionen einsetzen. Zwei analytische Funktionen auf einem Intervall sind bereits dann identisch, wenn sie nur auf einem Teilintervall übereinstimmen.
|
Bemerkung: Sei und . Dann gilt
|
[5.12.13] |
Beweis: ist analytisch auf I und gleich 0 auf J. Also ist , d.h. .
|
Der Identitätssatz [5.12.13] schränkt die Plastizität der analytischen Funktionen deutlich ein. So gibt es z.B. keine analytische Funktion auf , die gleich 0 ist für und gleich 1 für (Es gibt keine analytischen Treppen!).
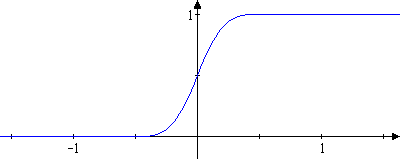
Im Abschnitt 9.12 konstruieren wir hochwertige Funktionen (sog. -Hüte), mit denen man eine solche Treppe herstellen kann.
|
