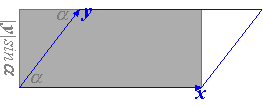
Bemerkung: Für gilt:
-
("Grassmannscher Entwicklungssatz")
-
("Jacobi-Identität")
-
-
("Lagrangesche Identität")
-
Beweis:
Zu 1.: Wir benutzen die Zerlegung
und berechnen damit:
Zu 2.: Wir benutzen den Grassmannschen Satz und erhalten für die drei Summanden:
Da das Skalarprodukt kommutativ ist, heben sich die sechs rechts stehenden Summanden auf. Das Ergebnis ist also der Nullvektor.
Zu 3.: Es reicht, die erste Gleichheit zu zeigen (Siehe auch den
nachfolgenden Kommentar). Das Überfahren der zweiten und dritten Zeile mit
dem Mauszeiger unterstützt die Überprüfung der Identität.
|
|
|
| |
|
| |
|
| |
|
|
|
. |
Zu 4.: Die Lagrangesche Identität erhalten wir aus 1. und 2.:
Die angegebene Gleichheit folgt nun mit der Kommutativität des
Skalarprodukts.
Zu 5.: Dies ist ein Spezialfall von 3. Man setzt dort und .
|