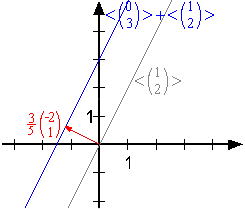9.16. Hesse-Darstellungen


9.16. Hesse-Darstellungen

In diesem Abschnitt betrachten wir ausschließlich affine Unterräume des $ℝ^{m}$ . Mit Hilfe der Orthonormalsysteme wird es uns gelingen, das Lot auf einen affinen Unterraum zu fällen, und so einen geometrisch ausgezeichneten Aufpunkt zur Verfügung zu stellen.

Zum zweiten soll in diesem Abschnitt das Zusammenspiel zwischen affinen Unterräumen und linearen Gleichungssystemen noch einmal beleuchtet werden. Dabei spielen Gleichungssysteme, die auf eine bestimmte Weise strukturiert sind, eine besondere Rolle bei der Berechnung der Lotvektoren.

Bemerkung und Definition: Ist

M = a + < w_{1}, \dots, w_{k} >

ein affiner Unterraum des

ℝ^{m}

, so gibt es genau einen Vektor

l \in M

, der in

< w_{1}, \dots, w_{k} >^{⊥}

liegt.

l heißt Lotvektor von M, seine Länge $| l |$ nennen wir den Nullabstand von M.

Beweis:

Zur Existenz: Da $ℝ^{m} = < w_{1}, \dots, w_{k} > \oplus < w_{1}, \dots, w_{k} >^{⊥}$ , gibt es eine Zerlegung für den Aufpunkt: $a = a' + a "$ . Wir setzen nun

l = a " \in < w_{1}, \dots, w_{k} >^{⊥}

und zeigen:

l \in M

: Da

l - a = a " - (a' + a ") = - a' \in < w_{1}, \dots, w_{k} >

, hat man:

l \in a + < w_{1}, \dots, w_{k} > \in M

. Man darf jetzt also den Aufpunkt von M austauschen:

M = l + < w_{1}, \dots, w_{k} >

Zur Eindeutigkeit: Ist $l'$ ein weiterer Vektor der genannten Art, so erhält man die folgenden Informationen:

\begin{array}{l} l' - l \in < w_{1}, \dots, w_{k} >, da l' \in M = l + < w_{1}, \dots, w_{k} >, \\ l' - l \in < w_{1}, \dots, w_{k} >^{⊥}, da l und l' zum Untervektorraum < w_{1}, \dots, w_{k} >^{⊥} gehören . \end{array}

Also ist $l' - l \in < w_{1}, \dots, w_{k} > \cap < w_{1}, \dots, w_{k} >^{⊥} = {0}$ , d.h.: $l = l'$ .

Beachte:

Die Fälle k=0 MathType@MTEF@5@5@+=feaafeart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrVepeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2da9iaaicdaaaa@3899@ und k=m MathType@MTEF@5@5@+=feaafeart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrVepeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2da9iaad2gaaaa@38D1@ sind schnell erledigt:
- Ist $k = 0$ , also $M = a + < \emptyset > = {a}$ , so ist a selbst der Lotvektor und $| a |$ der Nullabstand.
- Ist $k = m$ , also $M = ℝ^{m}$ , so ist 0 der Lotvektor und 0 der Nullabstand.
Für 0<k<m MathType@MTEF@5@5@+=feaafeart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrVepeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgYda8iaadUgacqGH8aapcaWGTbaaaa@3A8D@ werden wir die Berechnung des Lotvektors in zwei Schritte gliedern:
- Bestimmung des orthogonalen Komplements $< w_{1}, \dots, w_{k} >^{⊥}$ . Dies wird gelingen durch eine orthonomale Fortsetzung der Erzeugersequenz $w_{1}, \dots, w_{k}$ .
- Berechnung der zur Darstellung von l notwendigen Koeffizienten.

Die nachfolgenden Bemerkungen bereiten zunächst diese Schritte vor. Für den Rest dieses Abschnitts setzen wir stets $0 < k < m$ voraus. Ferner sei die Darstellung $a + < w_{1}, \dots, w_{k} >$ eines affinen Unterraums M stets so gewählt, dass die Erzeugersequenz $w_{1}, \dots, w_{k}$ linear unabhängig ist.

Bemerkung: Zu jeder linear unabhängigen Sequenz

w_{1}, \dots, w_{k}

des

ℝ^{m}

gibt es eine ON-Sequenz

n_{k + 1}, \dots, n_{m}

, so dass

< w_{1}, \dots, w_{k} >^{⊥} = < n_{k + 1}, \dots, n_{m} >

Die Sequenz

n_{k + 1}, \dots, n_{m}

nennen wir eine orthonormale Fortsetzung von

w_{1}, \dots, w_{k}

Beweis:

Über den Basisergänzungssatz und das Orthonormalisierungsverfahren gewinnen wir eine ON-Basis $n_{1}, \dots, n_{m}$ , mit $< w_{1}, \dots, w_{k} > = < n_{1}, \dots, n_{k} >$ . Also hat man nach Ergebnissen aus 9.15:

< w_{1}, \dots, w_{k} >^{⊥} = < n_{1}, \dots, n_{k} >^{⊥} = < n_{k + 1}, \dots, n_{m} >

Beachte:

Da $< w_{1}, \dots, w_{k} >$ ein Untervektorraum ist, gilt für eine orthonormale Fortsetzung von $w_{1}, \dots, w_{k}$ auch:

$< w_{1}, \dots, w_{k} > = < w_{1}, \dots, w_{k} >^{⊥ ⊥} = < n_{k + 1}, \dots, n_{m} >^{⊥}$ .
Zur konkreten Berechnung einer orthonormalen Fortsetzung n k+1 ,…, n m MathType@MTEF@5@5@+=feaafeart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrVepeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaBaaaleaacaWGRbGaey4kaSIaaGymaaqabaGccaGGSaGaeSOjGSKaaiilaiaad6gadaWgaaWcbaGaamyBaaqabaaaaa@3E32@ sind im allgemeinen Fall zwei Schritte durchzuführen:
1. Über die Gleichung $< w_{1}, \dots, w_{k} >^{⊥} = K e r (\begin{matrix} w_{1} \\ ⋮ \\ w_{k} \end{matrix})$ errechnet man per Gauß-Algorithmus den Senkrechtraum $< w_{k + 1}, \dots, w_{m} >$ .
2. Die gerade gewonnene Erzeugersequenz $w_{k + 1}, \dots, w_{m}$ wird orthonormalisiert.

Aufgabe: Ermittle zu den folgenden Sequenzen jeweils eine orthonormale Fortsetzung.

(\begin{matrix} 4 \\ - 3 \end{matrix})

(\begin{matrix} 1 \\ 2 \\ 1 \end{matrix})

(\begin{matrix} 0 \\ 2 \\ 2 \\ 1 \end{matrix}), (\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix})

Die Errechnung einer orthonormalen Fortsetzung ist, die Beispiele zeigen dies deutlich, ist i.a. recht aufwendig. In zwei Sonderfällen jedoch gibt es eine schnelle Methode, eine orthonormale Fortsetzung zu finden:

Bemerkung:

Ist w eine linear unabhängige Sequenz der Länge 1 in $ℝ^{2}$ , so ist ${(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})}^{°}$ eine orthonormale Fortsetzung von w.
Ist v,w eine linear unabhängige Sequenz der Länge 2 in $ℝ^{3}$ , so ist $(v \times w) °$ eine orthonormale Fortsetzung von v,w.
Dabei ist das Vektorprodukt (oder auch Kreuzprodukt) der Vektoren v und w gegeben durch

$v \times w = (\begin{matrix} v_{2} w_{3} - v_{3} w_{2} \\ - v_{1} w_{3} + v_{3} w_{1} \\ v_{1} w_{2} - v_{2} w_{1} \end{matrix})$ .

Beweis:

Zu 1.: Mit w ist auch $(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})$ von 0 verschieden, so dass ${(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})}^{°}$ wohldefiniert ist. Die Rechnung $w_{1} w_{2} + w_{2} (- w_{1}) = 0$ bestätigt $w ⊥ {(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})}^{°}$ und damit

< w > = < {(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})}^{°} >

Zu 2.: Der Beweis ergibt sich aus den folgenden Eigenschaften des Vektorprodukts:

\begin{matrix} v, w linear unabhängig \Rightarrow v \times w \neq 0 \\ v \times w ⊥ v \land v \times w ⊥ w . \end{matrix}

Diese und weitere Eigenschaften sind auf einer eigenen Seite notiert und nachgewiesen.

Bemerkung und Bezeichnung: Ist

M = a + < w_{1}, \dots, w_{k} >

ein affiner Unterraum des

ℝ^{m}

, so gilt für jede orthonormale Fortsetzung

n_{k + 1}, \dots, n_{m}

von

w_{1}, \dots, w_{k}

x \in M \Leftrightarrow (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) (x - a) = 0

Die Vektoren $n_{k + 1}, \dots, n_{m}$ bezeichnen wir in diesem Zusammenhang als Normalenvektoren von M und nennen das Gleichungssystem eine Hesse-Darstellung von M.

Beweis:

\begin{array}{l} x \in M & \Leftrightarrow x - a \in < w_{1}, \dots, w_{k} > = < n_{k + 1}, \dots, n_{m} >^{⊥} = K e r (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) \\ \Leftrightarrow (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) (x - a) = 0 . \end{array}

Beachte:

Neben dem ursprünglichen nennen wir auch das Gleichungssystem

$(\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) x = (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) a$

eine Hesse-Darstellung von M.
Eine Hesse-Darstellung von $M = a + < w_{1}, \dots, w_{k} >$ ist also im Prinzip eine Darstellung von M als Lösungsmenge eines linearen Gleichungssystems. Die dabei auftretende Matrix ist eine $(m - k) \times m$ - Matrix, deren Zeilenvektoren ein ON-System bilden.
Hyperebenen des $ℝ^{m}$ besitzen einzeilige Hesse-Darstellungen, denn für $k = m - 1$ hat man: $m - k = 1$ .
Das gerade erreichte Ergebnis läßt eine vollständige Charakterisierung der affinen Unterräume zu. Wir wissen bereits, dass die nicht-leeren Lösungsmengen linearer Gleichungssysteme stets affine Unterräume sind. Der Satz über die Hesse-Darstellungen zeigt nun, dass ein affiner Unterraum M, falls $0 < \dim M < m$ , auch nur so gewonnen werden kann. Ist $M = {a}$ ein Punkt, so ist M die Lösungsmenge von $(δ_{i j}) x = a$ . Ist $M = ℝ^{m}$ , so ist M die Lösungsmenge von $(0) x = 0$ . Man hat also insgesamt für eine nicht-leere Teilmenge $M \subset ℝ^{m}$ :

M ist ein affiner Unterraum $\Leftrightarrow$ M ist Lösungsmenge eines linearen Gleichungssystems.

Mit Hilfe einer Hesse-Darstellung, bzw. den damit gegebenen Normalenvektoren, ist es nun leicht, den Lotvektor und den Nullabstand zu berechnen:

Bemerkung: Sind

n_{k + 1}, \dots, n_{m}

Normalenvektoren des affinen Unterraums

M = a + < w_{1}, \dots, w_{k} >

, so gilt für den Lotvektor l:

$l = (n_{k + 1} \cdot a) n_{k + 1} + \dots + (n_{m} \cdot a) n_{m}$ .
$| l | = | (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) a | = {(n_{k + 1} \cdot a)}^{2} + \dots + {(n_{m} \cdot a)}^{2}$ .

Beweis:

Zu 1.: Da der Lotvektor l eindeutig bestimmt ist, reicht es zu zeigen:

(n_{k + 1} \cdot a) n_{k + 1} + \dots + (n_{m} \cdot a) n_{m} \in M \cap < w_{1}, \dots, w_{k} >^{⊥}

Nach Konstruktion ist $(n_{k + 1} \cdot a) n_{k + 1} + \dots + (n_{m} \cdot a) n_{m} \in < n_{k + 1}, \dots, n_{m} > = < w_{1}, \dots, w_{k} >^{⊥}$ .
Die Zeilenvektoren der Matrix $(\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix})$ bilden ein ON-System. Wendet man eine solche Matrix auf einen Vektor $x \in < n_{k + 1}, \dots, n_{m} >$ an, so erhält man nach einem Ergebnis in 9.15 genau den Koordinatenvektor von x:

$(\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) ((n_{k + 1} \cdot a) n_{k + 1} + \dots + (n_{m} \cdot a) n_{m}) = (\begin{matrix} n_{k + 1} \cdot a \\ ⋮ \\ n_{m} \cdot a \end{matrix}) = (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) a$ .

Damit aber ist $(n_{k + 1} \cdot a) n_{k + 1} + \dots + (n_{m} \cdot a) n_{m} \in M$ .

Zu 2.: Der Lotvektor l gehört zu M, erfüllt also die Hesse-Darstellung von M. Die Matrix $(\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix})$ operiert auf dem Erzeugnis ihrer Zeilenvektoren längentreu. Also hat man insgesamt:

$| l | = | (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) l | = | (\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) a |$ .

Beachte:

Der Lotvektor ist eine Linearkombination der Normalenvektoren $n_{k + 1}, \dots, n_{m}$ von M. Die Koeffizienten sind dabei die Skalarprodukte $n_{j} \cdot a$ .
Der Nullabstand von M lässt sich auch durch die Länge des Vektors $(\begin{matrix} n_{k + 1} \\ ⋮ \\ n_{m} \end{matrix}) a$ berechnen.
Ist M eine Hyperebene, also $k = m - 1$ , so schreibt man meist n statt $n_{m}$ . In diesem Fall ist $(n) a = n \cdot a$ eine reelle Zahl und der Nullabstand direkt gegeben durch:

$| n \cdot a |$ .

Wir betrachten nun einige Beispiele. Für den $ℝ^{2}$ und den $ℝ^{3}$ nutzen wir dabei die oben vorgestellten konstruktiven Möglichkeiten zur Ermittlung einer orthonormalen Fortsetzung!

Beispiel 1 (Geraden in

ℝ^{2}

): Ist

g = a + < w >

eine Gerade in

ℝ^{2}

, so ist

n = {(\begin{matrix} w_{2} \\ - w_{1} \end{matrix})}^{°} = \frac{1}{| w |} (\begin{matrix} w_{2} \\ - w_{1} \end{matrix})

ein Normalenvektor von g und die Gleichungen (die Matrix ( n ) ist hier einzeilig!)

\begin{matrix} (\begin{matrix} \frac{w_{2}}{| w |} & - \frac{w_{1}}{| w |} \end{matrix}) (x - a) = 0 \\ (\begin{matrix} \frac{w_{2}}{| w |} & - \frac{w_{1}}{| w |} \end{matrix}) x = (\begin{matrix} \frac{w_{2}}{| w |} & - \frac{w_{1}}{| w |} \end{matrix}) a \\ \frac{w_{2}}{| w |} x_{1} - \frac{w_{1}}{| w |} x_{2} = \frac{w_{2} a_{1} - w_{1} a_{2}}{| w |} \end{matrix}

sind die verschiedenen Formen einer Hesse Darstellung von g. Ferner ist

l = (n \cdot a) n = \frac{w_{2} a_{1} - w_{1} a_{2}}{| w |} \cdot \frac{1}{| w |} (\begin{matrix} w_{2} \\ - w_{1} \end{matrix}) = \frac{1}{| w |^{2}} (\begin{matrix} w_{2}^{2} a_{1} - w_{1} w_{2} a_{2} \\ - w_{1} w_{2} a_{1} + w_{1}^{2} a_{2} \end{matrix})

der Lotvektor und

| l | = | (n \cdot a) n | = \frac{| w_{2} a_{1} - w_{1} a_{2} |}{| w |}

der Nullabstand von g.

So errechnet man etwa für

g = (\begin{matrix} 0 \\ 3 \end{matrix}) + < (\begin{matrix} 1 \\ 2 \end{matrix}) >

\begin{matrix} n = {(\begin{matrix} 2 \\ - 1 \end{matrix})}^{°} = \frac{1}{\sqrt{5}} (\begin{matrix} 2 \\ - 1 \end{matrix}), \\ (n) a = (\begin{matrix} \frac{2}{\sqrt{5}} & - \frac{1}{\sqrt{5}} \end{matrix}) (\begin{matrix} 0 \\ 3 \end{matrix}) = - \frac{3}{\sqrt{5}} . \end{matrix}

Also sind die Gleichungen

\begin{matrix} (\begin{matrix} \frac{2}{\sqrt{5}} & - \frac{1}{\sqrt{5}} \end{matrix}) (x - (\begin{matrix} 0 \\ 3 \end{matrix})) = 0 \\ (\begin{matrix} \frac{2}{\sqrt{5}} & - \frac{1}{\sqrt{5}} \end{matrix}) x = - \frac{3}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} x_{1} - \frac{1}{\sqrt{5}} x_{2} = - \frac{3}{\sqrt{5}} \end{matrix}

Hesse-Darstellungen von g.

l = - \frac{3}{\sqrt{5}} \frac{1}{\sqrt{5}} (\begin{matrix} 2 \\ - 1 \end{matrix}) = \frac{3}{5} (\begin{matrix} - 2 \\ 1 \end{matrix})

ist der Lotvektor und

| l | = \frac{3}{\sqrt{5}}

ist der Nullabstand von g.

Beispiel 2 (Ebenen in

ℝ^{3}

): Ist

E = a + < v, w >

eine Ebene in

ℝ^{3}

, so ist

n = (v \times w) °

ein Normalenvektor von E und (da hier die Matrix ( n ) einzeilig ist) sind

\begin{matrix} (v \times w) ° (x - a) = 0 \\ (v \times w) ° x = (v \times w) ° a \end{matrix}

die verschiedenen Formen einer Hesse Darstellung von E. Ferner ist

l = (n \cdot a) n = ((v \times w) ° \cdot a) (v \times w) ° = \frac{(v \times w) ° \cdot a}{| v \times w |^{2}} (v \times w)

der Lotvektor und

| l | = | n \cdot a | = | \frac{(v \times w) \cdot a}{| v \times w |} |

der Nullabstand von E.

So hat man etwa für $E = (\begin{matrix} 2 \\ - 1 \\ 2 \end{matrix}) + < (\begin{matrix} 0 \\ - 2 \\ 3 \end{matrix}), (\begin{matrix} 1 \\ 0 \\ - 3 \end{matrix}) >$ :