7.11. Extremal Problems

Applying math often comprises the task to find a certain setting for some parameters of a process to ensure an optimal result (e.g. shortest distance, highest profit, lowest consumption). In many cases our techniques of detecting global extreme points will enable us to find a calculative solution.

For a simple example to start with we consider rectangles with a fixed perimeter U. There are lots of those rectangles and they all differ in their area as can be checked by dragging the blue anchor in the sketch below.

To that end we survey all the areas encountered, in other words we consider the function A given by

The variables x and  y however are not independent from each other as the side condition, that is setting the perimeter ${\displaystyle U>0}$ as fixed, forces x and  y into a distinct relationship:

Thus we may substitute the variable  y in [1] by some term of x. Considering that the width x may only take values between 0 and ${\displaystyle \frac{U}{2}}$ we get the following definition for the target function  ${\displaystyle A:[\mathrm{0,}\frac{U}{2}]\to ℝ}$

Looking for a greatest area now means searching for a global maximum for A. Such a maximum point will exist as A is continuous on a closed interval (see[6.6.5]). It could be one of the boundary points or a local maximum point in the interior of the domain of A.

The latter case is easily dealt with using our criteria for twice differentiable functions: As

and ${\displaystyle {A^{\prime }}^{\prime }}$ we find a single local maximum in the interior namely at ${\displaystyle \frac{U}{4}}$ with a value of

By comparison with the boundary values  ${\displaystyle A(0)=0}$ and ${\displaystyle A(\frac{U}{2})=0}$ we finally see that the rectangle with ${\displaystyle x=\frac{U}{4}}$ and ${\displaystyle y=\frac{U}{4}}$ (according to [2]) has the greatest area. Thus we proved the well known fact:

This result is a special case of the so called isoperimetric problem, i.e. to find among all laminae with a fixed (appropriate) perimeter the one(s) with the greatest area. Although it is quite obvious that this will be a circle it is far from simple to prove this. For more information see Viktor Blasjö: The Isoperimetric Problem, Amer. Math. Monthly 112, pp. 526-566.

A similar problem, often encountered in economic activities, is called the packaging problem: How to gain a maximal volume from a fixed surface? As an example we create a box (no lid) of greatest volume from a rectangular cardboard sized a×b (${\displaystyle a\ge b>0}$). We just cut out four squares of width x as shown in the drawing and then flip up the resulting straps. Our cardboard is sized a = 240px and b = 180px.

introduces the target function  ${\displaystyle V:[\mathrm{0,}\frac{b}{2}]\to ℝ}$ directly without quoting the side condition

i

A detailed notation, like for instance V(x) = length·width·x, with side condition "length = a − 2x and width = b − 2x", turns out to be unnecessary laborious in straightforward situations like this.

explicitly. Next we find the local extreme points for V within the interior of the domain interval. From

we get:  ${\displaystyle V^{\prime }(x)=0\iff x=\frac{1}{6}(a+b)\pm \frac{1}{6}\sqrt{{(a+b)}^2-3ab}=\frac{1}{6}(a+b\pm \sqrt{{(a-b)}^2+ab})}$. As

the first root does not belong to ${\displaystyle ]0,\frac{b}{2}[}$ in contrast to the second one because here we have:

Furthermore  ${\displaystyle {V^{\prime }}^{\prime }(\frac{1}{6}(a+b-\sqrt{{(a-b)}^2+ab}))=-\sqrt{{(a-b)}^2+ab}<0}$ in fact proves the second root to be a local maximum point.

And according to [4] twice of its value is less than b, and therefor less than a as well. Thus [3] guarantees

which means that ${\displaystyle \frac{1}{6}(a+b-\sqrt{{(a-b)}^2+ab})}$ leaves the comparison test with both boundary values ${\displaystyle V(0)=0=V(\frac{b}{2})}$ as a global maximum point. In our example this calculates to a (rounded) value of 34px.

In physics the behaviour of systems is often controlled in such a way that a certain variable reaches its minimum value. Forced by energy balancing the shape of a soap bubble for instance will always have a minimal surface and thus will come as a ball. Often this minimization principle is also found as the general idea behind the laws of physics. We will demonstrate this with the law of reflection:

If a signal is reflected off a mirror plane the angle of incidence and angle of reflexion are equal.

We will now prove that this holds for a reflection if and only if the signal follows the shortest way from sender to receiver.

Proposition:  Let α be the angle of incidence and β the angle of reflection of an arbitrary reflection. Then the following holds: ${\displaystyle \alpha =\beta \iff }$the path of the signal has a minimal length. [7.11.2] Proof:  We introduce a suitable coordinate plane that locates the sender at (0,s), the receiver at (a,b) and the reflection point at (x,0). For ${\displaystyle a,b,s,x>0}$ we thus have the following scene:   animation ↔ trigonometry s b xa The length ${\displaystyle l(x)}$ of the path depends on the position of the reflection point and is calculated according to Pythagoras' theorem (choose option trigonometry) like this: ${\displaystyle l(x)=\sqrt{x^2+s^2}+\sqrt{{(a-x)}^2+b^2},x\in [0,a]}$ l is twice differentiable and its derivatives are ${\displaystyle \begin{array}{ll}\hfill l^{\prime }(x)=& \frac{x}{\sqrt{x^2+s^2}}-\frac{a-x}{\sqrt{{(a-x)}^2+b^2}}\text{[5]}\hfill \\ \hfill {l^{\prime }}^{\prime }(x)=& \frac{s^2}{{\sqrt{x^2+s^2}}^3}+\frac{b^2}{{\sqrt{{(a-x)}^2+b^2}}^3}>0\text{[6]}\hfill \end{array}}$ [5] now yields the following equivalence for all ${\displaystyle x\in ]0,a[}$: ${\displaystyle \begin{array}{ll}{l}^{\prime }(x)=0\hfill & \iff \frac{x}{\sqrt{x^2+s^2}}=\frac{a-x}{\sqrt{{(a-x)}^2+b^2}}\hfill \\ \hfill & \iff \sin \alpha =\sin \beta \hfill \\ \hfill & \iff \alpha =\beta \text{[7]}\hfill \\ \hfill & \iff \tan \alpha =\tan \beta \hfill \\ \hfill & \iff \frac{s}{x}=\frac{b}{a-x}\hfill \\ \hfill & \iff x=\frac{a\cdot s}{b+s}\hfill \end{array}}$ Due to [6] we thus know: l has a single local minimum point within ${\displaystyle ]0,a[}$ namely at ${\displaystyle \frac{a\cdot s}{b+s}}$  i Consider:  ${\displaystyle 0<\frac{a\cdot s}{b+s}<\frac{a\cdot s}{s}=a}$. . This is also the only global minimum point as a comparison with the boundary values ${\displaystyle \begin{array}{l}l(0)=s+\sqrt{a^2+b^2}\hfill \\ l(a)=\sqrt{a^2+s^2}+b\hfill \end{array}}$ will show. From ${\displaystyle \begin{array}{ll}l(\frac{a\cdot s}{b+s})\hfill & =\sqrt{\frac{a^2{s}^2}{{(b+s)}^2}+s^2}+\sqrt{{(a-\frac{a\cdot s}{b+s})}^2+b^2}\hfill \\ \hfill & =\frac{s}{b+s}\sqrt{a^2+{(b+s)}^2}+\frac{b}{b+s}\sqrt{a^2+{(b+s)}^2}\hfill \\ \hfill & =\sqrt{a^2+{(b+s)}^2}\hfill \end{array}}$ and the estimates ${\displaystyle b=\sqrt{b^2}<\sqrt{a^2+b^2}}$ and ${\displaystyle s=\sqrt{s^2}<\sqrt{a^2+s^2}}$ respectively we get ${\displaystyle \begin{array}{ll}1.\hfill & a^2+{(b+s)}^2<a^2+b^2+s^2+2s\sqrt{a^2+b^2}={(s+\sqrt{a^2+b^2})}^2\hfill \\ \Rightarrow \hfill & \sqrt{a^2+{(b+s)}^2}<s+\sqrt{a^2+b^2}\hfill \\ \hfill & \hfill \\ 2.\hfill & a^2+{(b+s)}^2<a^2+b^2+s^2+2b\sqrt{a^2+s^2}={(\sqrt{a^2+s^2}+b)}^2\hfill \\ \Rightarrow \hfill & \sqrt{a^2+{(b+s)}^2}<\sqrt{a^2+s^2}+b\hfill \end{array}}$ All in all we thus have: the path has a minimal length${\displaystyle \iff x=\frac{a\cdot s}{b+s}}$ which finally proves the assertion [7.11.2] due to [7].

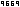7.10.

7.12.