7.10. Geometric Properties of Differentiable Functions
It is evident now from the previous chapter that the behaviour of a function f is controlled by its own derivative with the mean value theorem being the "controlling agent".
Now we are going to study two geometric behaviours in more detail, monotony and curvature. It will turn out that monotony is related to the first derivative and curvature to the second.
|
Definition: A function is called
increasing (or monotonic increasing) on , if the implication
|
[7.10.1] |
decreasing (or monotonic decreasing) on , if the implication
|
[7.10.2] |
holds for all . f is called strictly increasing on B, if the conclusion in [7.10.1] could be tightened to . The property strictly decreasing is introduced appropriately.
Usually the term "on B" is only used if .
|
Consider:
-
Obviously the constant functions are increasing and decreasing simultaneously. And they are the only ones of that kind, because: If is monotone in both directions any two points will satisfy
.
Thus any two values of f coincide. For a fixed for instance we have: for all .
-
Occasionally it is an advantage to use a slightly modified version of the monotony condition. Note that
-
[7.10.1] is equivalent to: [1]
-
[7.10.2] is equivalent to: [2]
[1] and [2] however allow to restate the monotony condition in terms of difference quotient functions:
|
Proposition: A function is
monotonic increasing on , if and only if any two different points satisfy
|
[7.10.3] |
monotonic deacreasing on , if and only if any two different points satisfy
|
[7.10.4] |
Proof: As both assertions are similar to prove, we only show the first one.
"": Let f be increasing. From [1] we see that for both differences, and , have the same sign, so that the quotient is always positive.
"": If now , then because otherwise we would have in contrast to the premise.
|
For differentiable functions on intervals the above result will lead to the monotony test, a method to characterise the monotony of f by its derivative behaviour. The monotony test puts the first derivative into a geometric perspective.
|
Proposition (monotony test): Let f be differentiable on an interval I, i.e. . Then we have
- f is increasing on I
|
[7.10.5] |
- f is decreasing on I
|
[7.10.6] |
Proof: Again we only deal with 1.
"": If f is increasing we know from [7.10.3] that
for all .
According to [6.9.4] we thus get .
"": Now take such that . Due to the mean value theorem [7.9.5] there is an satisfying
.
|
Consider:
Note that the direction "" provided the typical context for an application of the mean value theorem. Further, the details in the proof show that
-
the required derivative behaviour is actually only needed at interior points of I.
-
the direction "" is valid for strict monotony as well, i.e. we have:
-
for all interior x of If is strictly increasing on I.
-
for all interior x of If is strictly decreasing on I.
We cannot prove the complete equivalence however as is documented by the strictly increasing function : .
The monotony now widens the options to confirm a local extreme point and this will result in a further sufficient criterion (cf. the necessary criterion [7.9.2] and the sufficient criterion [7.9.17] for -functions). As a start we observe that a transition point between two different monotony domains has to be an extreme point.
|
Proposition: has a local extremum at if there is an such that f has a different monotony behaviour on the relative semi-neighbourhoods
and .
|
[7.10.7] |
The reverse does not hold.
Proof: We assume f is increasing on and decreasing on . That means for all

i  |
|
|
:
which actually says that f has a local maximum at a.
A counter example will prove that the reverse is false. The indicator function 
i  |
|
has a global minimum at 0, but fails to be monotone on any interval.
|
A new sufficient criterion (" changes the sign at its zero a") for differentiable functions on intervals is now available.
|
Proposition: A function has a local extremum at if there is an such that has a different sign on the semi-neighbourhoods
and
|
[7.10.8] |
The reverse is not true.
Proof: If the sign of differs on the intervals and , let's say for all and for all , f has a different monotony behaviour on these intervals according to [7.10.5./6.]. Due to [7.10.7] f thus has a local extremum at a.
The function defined by
shows that the reverse of [7.10.8] does not hold: f is differentiable with
and has a global minimum at 0. But changes the sign arbitrary often in each semi-neighbourhood of 0. We show this exemplarily for a semi-neighbourhood to the right. To that end we calculate for an arbitrary the values and using the addition theorems for sin and cos [4.3.*]. With
and we now calculate
|
We turn to a second geometric aspect which is illustrated by the two functions below.
|
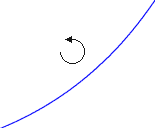 
In the depicted section both have the same end points and both are monotone in the same direction, namely increasing. Nevertheless they differ in their appearance significantly, actually in the way they are curved. The first function is curved to the left whereas the second one is curved to the right.
We can visualise this different curvature using the secant test: Any secant to the function sits above the graph in the first case and below in the second. It is this oberservation that is behind the following definition.
|
|
Definition: A function is called
convex (or curved to the left or said to have a positive curvature) on if
|
[7.10.9] |
concave (or curved to the right or said to have a negative curvature) on if
|
[7.10.10] |
holds for all such that .
If [7.10.9] even allows instead of , f is called strictly convex on B. strictly concave is defined appropriately.
We omit the the phrase "on B" if .
|
Consider:
-
Multiplying [7.10.9] by −1 yields the correlation
f convex concave.
-
A linear function f is curved to the left and to the right simultaneously, as for any two different points f may be represented as as well. Otherwise, if a function is convex and concave as well we have, as a start, for any and every :
[3]
and thus especially:
As we can restate [3] independently of n:
.
But this identity is valid for all x as for every x there will be an such that .
f is thus linear.
We now concentrate on convex functions. All the results are transferable to concave functions as well, and, with only rare exceptions, even to the strict case.
Slightly rearranging [7.10.9] (note: !) yields
, [4]
as an equivalent condition for the convexity of f. Considering further that the lines
and
are the same, i.e. that [7.10.9] is replaceable by
, we get another convexity test (note: !):
[5]
Finally, combining [4] and [5] results in a third, more versatile convexity condition.
|
Proposition: is convex on if and only if for any such that the following condition holds:
|
[7.10.11] |
Proof: For all the following inequalities are equivalent:
|
Now we are prepared, at least for differentiable functions on intervals, to prove some more comfortable convexity criteria.
|
Proposition:
-
If , then:
f is convex is monotonic increasing
|
[7.10.12] |
-
If , then:
f is convex
|
[7.10.13] |
Proof:
1. ► For the direction "" we take two points a and b of I such that . Due to [4] and [5] we have for all :
.
As and (see [6.9.1] for details) we thus know:
,
which in fact proves that is increasing.
"": Now we take a fixed point , . According to the mean value theorem [7.9.4] we find two points nested , such that, due to the monotony of , the following estimate holds:
.
[7.10.11] now guarantees the convexity of f.
2. ► follows immediately from 1. due to [7.10.5].
|
Consider:
-
As common with the mean value theorem the direction "" is also valid for a strict version of [7.10.12/13]:
strictly increasing f strictly convex
f strictly convex
"" however fails in the strict case.
[7.10.7] illustrated the role of transition points between two different monotony domains. We should pay attention to transition points between two different curvature domains as well.
|
Definition: Let be an interior point of I. A function is said to have an inflection point at a if there is an such that the curvature sign of f differs on the semi-neighbourhoods
and .
|
[7.10.14] |
If in addition f is differentiable at a and the inflection point is also called a saddle point for f. Saddle points are thus inflection points with a horizontal tangent.
|
Consider:
-
As a linear function is convex and concave simultaneously, its curvature sign changes at every point. Linear functions thus have an inflection point at each .
-
Due to [7.10.12] we have for -functions:
f has an inflection point at a changes its monotony behaviour at a. [6]
-
Due to [7.10.13] we have -functions:
f has an inflection point at a changes its sign at a. [7]
[6] and [7] make it easy to find necessary existence criteria for inflection points.
|
Proposition: If has an inflection point at we have for any
-
-function:
has a local extremum at a.
|
[7.10.15] |
-
-function:
|
[7.10.16] |
In both cases the reverse does not hold.
Proof:
1. ► According to [6] the monotony behaviour of changes at a so that has a local extremum at a due to [7.10.7].
We need a counter example to prove that the reverse is not valid. We turn back to the differentiable, thus continuous function introduced in [7.10.8] by
As f is continuous [8.1.5] guarantees that there will be a differentiable function such that . We read the properties of f proved in [7.10.8] now like this:
-
has a global minimum at 0.
-
does'nt change its sign at 0 so that g has no inflection point at 0 due to [7].
2. ► is an immediate consequence of [7.9.2] due to 1.
The non-constant power function is convex on the whole of according to [7.10.13] ( for all x! ) thus has no inflection point at all. Nevertheless we have .
|
We now get a sufficient criterion for -functions with the help of Taylor's formula [7.9.16]. The approach will be parallel to [7.9.17].
|
Proposition (sufficient criterion for -functions): Take and an interior point a of I such that
.
|
[7.10.17] |
Then we have:
-
If n + 2 is odd f has an inflection point at a.
-
If n + 2 is even f has no inflection point at a.
Proof: We apply Taylor's formula to the -function . Assuming will provide, due to continuity, an such that for all . For each of these x there is now an in between x and a such that
.
thus changes its sign at a iff n is odd. Due to [7] this is the assertion.
|
Consider:
We use the terms "convex" and "concave" to describe the quality of a curvature. Deciding if a function is curved to the left or curved to the right however does not provide any information of the curvature's quantity, i.e. we are unable to measure how small or how big the curvature at a certain point is.
It is only with circles that we have an idea how to measure curvature, namely by considering the radius: As the curvature looks the smaller the bigger the radius is, we will introduce the reciprocal of the radius as a psychological sound measure for the curvature of a circle.
If we succeed now to find an appropriate circle, the so called circle of curvature, that nestles perfectly to a given function f at a suitable point a we could take its radius as the radius of curvature of f at a.
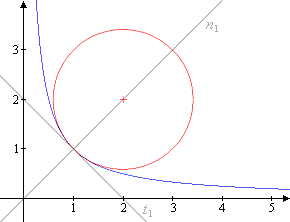
The sketch to the left shows the circle of curvature with respect to the reciprocal function at 1. The distance between its centre (2,2) and its boundary point (1,1), i.e. the radius of curvature calculates to in this case.
But how to construct such a ideal circle, how to find its centre and its radius? The first idea is to look for it among those circles that are attached vertically to f. Thus we will concentrate on circles through (a, f(a)) that have its centre on the normal , i.e. on the perpendicular to the tangent .
To pick the "right" one out of those we need to know the local geometry of the graph, so that the values of f in the vicinity of a are involved. When we constructed the tangent we used secants, auxiliary lines that resulted from considering additional points (x, f(x)). Analog to that we will introduce "secant circles" that have (x, f(x)) as an additional point. Subsequently we will calculate their centres as the insection points of the normal and the perpendicular bisector of the secant determined by a and x. The following interactive applet illustrates the concept quite convincing.
We now consider -functions at points a with a definite curvature. We will thus subsequently exclude inflection points and will assume that . Further we will markedly benefit from the vector notation in the calculations ahead. Tangent, normal and perpendicular bisector are thus presented like this:
|
Proposition: If and a is an interior point of I such that there are, without restriction, two points in between x and a for every such that the lines and intersect solely at
|
[7.10.18] |
Proof: As is continuous we know that for all x in an appropriate neighbourhood of a. Without restriction we assume .
To calculate the intersection we now use a method outlined in 9.9. For an arbitrary vector
the following equivalence accordingly holds:
Using Taylor's theorem [7.9.16] we find two points in between x and a such that
-
-
which allows to extend the equivalence [8] by
so that finally the unique solution is calculated to
.
|
Now we are able to analyse the limit behaviour of the intersection points which in fact are the centres of the secant circles. If x converges to a the intermediate points and are forced to do the same. Now that f is differentiable at a and are continuous at that point, the function has a limit at a:
.
Obviously this limit is a point on the normal and its distance to the boundary point (a, f(a)) calculates to
.
With these results we have achieved our aim: To describe curvature in quantitative terms.
|
Definition: For any and an interior point a of I such that the circle of curvature of f with respect to a is defined by its
centre of curvature
|
[7.10.19] |
and its
radius of curvature
|
[7.10.20] |
The number is called the curvature of f at a.
In case we additionally set and .
|
As an example we calculate the curvature data of the standard parabola and of a semi-circle with radius r centered at the origin. With the latter we expect all radii of curvature to coincide with r and all centres of curvature to be (0,0).
|
Example:
-
For we get:
-
For we initially have
.
and from that we calculate
|
|
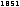 |
|


