6.6. Continuous Functions on Closed Intervals

As already mentioned briefly continuous functions unfold a special wealth of properties on closed intervals. This part deals solely with the intermediate value theorem and the extreme value theorem, two outstanding examples within this context. The results in this part are only valid for closed intervals. Furthermore they are completely confined to the real numbers due to the fact that all essential proofs use the completeness axiom, a feature only valid in

ℝ

Among all ordered fields $ℝ$ is the only one to satisfy the completeness axiom:

Every non-empty subset $A \subset ℝ$ bounded from above has a least upper bound, the supremum of A.

The supremum of A is a uniquely determined real number denoted by the symbol $\sup A$ . As an equivalent to the noted version we also may use the following one:

Every non-empty subset $A \subset ℝ$ bounded from below has a greatest lower bound, the infimum of A (in symbols $\inf A$ ).

Supremum and infimum have the following properties:

$x \leq \sup A for all x \in A$

$\inf A \leq x for all x \in A$

$x \leq s for all x \in A \Rightarrow \sup A \leq s$

$s \leq x for all x \in A \Rightarrow s \leq \inf A$

$A \subset [a, b] \Rightarrow \sup A \in [a, b]$

$A \subset [a, b] \Rightarrow \inf A \in [a, b]$

$y < \sup A \Rightarrow$ there is an $x \in A$ , $x > y$

$y > \inf A \Rightarrow$ there is an $x \in A$ , $x < y$

$A \subset B \Rightarrow \sup A \leq \sup B$

$A \subset B \Rightarrow \inf A \geq \inf B$

The zero theorem, a special case of the intermediate theorem, is easily depicted: As the real x-axis has no gaps any continuous function to cross this axis will do this by intersection.

Theorem (zero theorem): Take $f \in C^{0} ([a, b])$ . If its values at a and b differ in their algebraic sign, e.g. $f (a) < 0 < f (b)$ , f has a zero within the interior of $[a, b]$ , i.e. there is a number $\tilde{x} \in] a, b [$ such that

f (\tilde{x}) = 0

[6.6.1]

Proof: Let's outline the basic idea first: If we could choose the greatest x from all $x \in [a, b]$ with a negative value we would only find numbers with a positive value right to that position. It is at this transition where we expect a zero for f.

Thus we consider the set

A ≔ {x \in [a, b] | f (x) \leq 0} \subset [a, b]

A is non-empty, infact a is member of A as $f (a) < 0$ . Being a subset of $[a, b]$ A turns out to be bounded thus has a supremum according to the completeness axiom.

For $\tilde{x} ≔ \sup A$ we have $\tilde{x} \in [a, b]$ and as there are no elements of A beyond $\tilde{x}$ we know that

f (x) > 0 for all x \in] \tilde{x}, b]

[0]

Excluding the options $f (\tilde{x}) > 0$ and $f (\tilde{x}) < 0$ now proves the assertion: $f (\tilde{x}) = 0$ :

If $f (\tilde{x}) > 0$ , in particular $\tilde{x} \neq a$ , proposition [6.4.1] provides a relative $ε$ -neighbourhood ${[a, b]}_{\tilde{x}, ε} = [a, b] \cap] \tilde{x} - ε, \tilde{x} + ε [$ such that

$f (x) > 0 for all x \in {[a, b]}_{\tilde{x}, ε}$

As $\tilde{x} \neq a$ we find a number $y < \tilde{x}$ inside $[a, b]$ such that $f (x) > 0$ for all $x \in [y, \tilde{x}]$ . Combining this with the information in [0] yields $A \subset [a, y [$ and thus the contradiction $\tilde{x} = \sup A \leq y < \tilde{x}$ .
If $f (\tilde{x}) < 0$ , in particular $\tilde{x} \neq b$ , we employ [6.4.1] again to get a relative $ε$ -neighbourhood ${[a, b]}_{\tilde{x}, ε} = [a, b] \cap] \tilde{x} - ε, \tilde{x} + ε [$ such that

$f (x) < 0 for all x \in {[a, b]}_{\tilde{x}, ε}$

With $\tilde{x} \neq b$ we find an $x > \tilde{x}$ inside $[a, b]$ such that $f (x) < 0$ in contradiction to [0].

So we have $f (\tilde{x}) = 0$ which also proves that $\tilde{x} \in] a, b [$ .

Consider: The premise of the zero theorem cannot be lessened. For example

$\frac{1}{X}$ is continuous on ${[- 1, 1]}^{\neq 0}$ but has no zero.
$H - \frac{1}{2}$ is discontinuous on $[- 1, 1]$ and has no zero.
$(X^{2} - 2) | ℚ$ is continuous on $[0, 2] \cap ℚ$ and has no zero.

The zero theorem opens the door to a different approach to solve equations. As only few equations have exactly computable roots the need for approximation methods is obvious. Often these methods are iterative, producing a sequence of roots with increasing accuracy.

A common example is the iterated bisection of intervals, a method that isolates the root within intervals of decreasing diameters. As an example we consider the equation

x^{3} + x - 1 = 0

Its roots are the zeros of the continuous function $f = X^{3} + X - 1$ . The zero theorem now allows to argue as follows:

As $f (0) = - 1$ and $f (1) = 1$ f has to have a zero within the initial interval $[0, 1]$ .
For its midpoint $x_{m} = 0.5$ we have $f (0.5) = - 0.375$ . Consequently f has a zero within the right subinterval $[0.5, 1]$ .
Iterating the previous step will yield a sequence of zero intervals with halfed diameters in each step.

The following table shows the initial situation. Iterating about 20 times will overstrain the computers precision bounds. Let us with steps:

step \| $f (x_{m}) = x_{m}^{3} + x_{m} - 1$ \| zero interval

With , the last zero interval's midpoint, we now got a number not more than 2 = units away from the 'real' zero. Thus we have found a root accurate to at least decimal places.

Iterated bisection of intervals is quite a simple approximation method with no special emphasis on its rate. With more sophisticated methods (such as e.g. the regula falsi or Newton's method) running times could be improved.

Turning now back to the actual issue of this part we will prove the intermediate value theorem. Using the common 'difference trick' it comes easily from the zero theorem.

Theorem (intermediate value theorem): Take $f \in C^{0} ([a, b])$ and $c \in ℝ$ . If c is intermediate between $f (a)$ and $f (b)$ , for example $f (a) < c < f (b)$ , than there is an $\tilde{x} \in] a, b [$ such that

f (\tilde{x}) = c

[6.6.2]

Proof: The continuous function $f - c \in C^{0} ([a, b])$ satisfies $f - c (a) < 0 < f - c (b)$ . Thus the zero theorem [6.6.1] provides a suitable $\tilde{x} \in] a, b [$ such that

f - c (\tilde{x}) = 0 \Leftrightarrow f (\tilde{x}) = c

The difference trick could also be employed for the comparison of two functions: Two continuous functions are to intersect if their values at the interval's endpoints are differently orientated.

Task: Take $f, g \in C^{0} ([a, b])$ such that $f (a) < g (a)$ and $f (b) > g (b)$ .

Show: f and g have an intersection point in the interior of $[a, b]$ i.e. there is an $\tilde{x} \in] a, b [$ holding

f (\tilde{x}) = g (\tilde{x})

[6.6.3]

Proof: ?

Preparing the extreme value theorem we now prove that continuous functions on closed intervals are always bounded. In many cases this is a helpful property of continuous functions.

Theorem: If $f \in C^{0} ([a, b])$ then f is bounded, i.e. there is a number c such that

| f (x) | \leq c for all x \in [a, b]

[6.6.4]

Proof: According to [6.5.5] f is uniformly continuous on $[a, b]$ . Thus there is a $δ > 0$ such that

| x - y | < δ \Rightarrow | f (x) - f (y) | < 1

[1]

for all $x, y \in [a, b]$ . As $ℝ$ is an archimedean field
i

That means: $ℕ$ is an unbounded subset of $(ℝ, \leq)$ . So there will be a greatest natural k such that $k \leq \frac{b - a}{δ}$ .

the set $[a, b] \cap {a + n δ | n \in ℕ}$ is finite, thus we find a $k \in ℕ$ such that

[a, b] \cap {a + n δ | n \in ℕ} = {a + 0 \cdot δ, \dots, a + k \cdot δ}

From that we get the estimate

| f (x) | \leq c ≔ \max {| f (a + 0 \cdot δ) |, \dots, | f (a + k \cdot δ |, | f (b) |} + 1

because for each $x \in [a, b [$ we find a number $i \leq k$ such that $x \in [a + i \cdot δ, a + (i + 1) \cdot δ [$ , i.e. $| x - (a + i \cdot δ) | < δ$ , so that [1] will ensure

\begin{array}{l} | f (x) | - | f (a + i \cdot δ) | \leq | f (x) - f (a + i \cdot δ) | \leq 1 \\ \Rightarrow & | f (x) | \leq | f (a + i \cdot δ) | + 1 \leq c \end{array}

So we know that continuous functions on closed intervals have bounds. The next theorem shows that some of these are even actual values.

Theorem (extreme value theorem): For each $f \in C^{0} ([a, b])$ there are two numbers $\underline{x}, \bar{x} \in [a, b]$ such that

f (\underline{x}) \leq f (x) \leq f (\bar{x}) for all x \in [a, b]

[6.6.5]

Proof: At first we show that a minimum value exists: Due to [6.6.4] we may use the number

c ≔ \inf {f (x) | x \in [a, b]}

which turns out to be a value of f. Certainly we have $c \leq f (x)$ [2] for all $x \in [a, b]$ and as there are no further bounds above c we find an $x_{n} \in [a, b]$ for each $n \in ℕ^{*}$ such that

c \leq f (x_{n}) < c + \frac{1}{n}

[3]

According to the Bolzano-Weierstrass theorem [5.8.6] the bounded sequence $(x_{n})$ has an accumulation point $\underline{x} \in [a, b]$ that could be represented as the limit of suitable subsequence: $\underline{x} = lim x_{k_{n}}$ .

Using [3] we get $c \leq f (x_{k_{n}}) < c + \frac{1}{k_{n}} \leq c + \frac{1}{n}$ . The nesting theorem [5.5.8] and the continuity of f now establish the equality

c = lim f (x_{k_{n}}) = f (lim x_{k_{n}}) = f (\underline{x})

Due to [2] $c = f (\underline{x})$ is thus a minimum value for f.

A maximum value is now easy to find: If $- f (\bar{x})$ is a minimum value for the continuous function $- f$ then $f (\bar{x})$ is a maximum value for f.

Consider:

The sine function on $[0,8 π]$ for example shows that a function could take its extreme values more than once. So uniqueness isn't guaranteed.
Also it is indispensable for the interval to be closed ( $\frac{1}{X}$ is unbounded on $] 0, 1]$ ) as well as for the function being continuous:

$f : x \mapsto {\begin{array}{l} 0 if x = 0 \\ \frac{1}{x} if x \in] 0,1] \end{array}$

for example has no maximum value.
Finally [6.6.6] is strictly confined to the reals: The function ${(X - 2)}^{2} | ℚ$ is continuous on $[0, 2] \cap ℚ$ but has no minimum value!

Combining the two major theorems of this part results in an interesting property of the domain of a continuous function.

Proposition: Continuous functions map intervals on intervals:

f \in C^{0} ([a, b]) \Rightarrow f ([a, b])

is an interval

[6.6.6]

Proof: According to [6.6.5] there are numbers $\underline{x}, \bar{x} \in [a, b]$ such that

f ([a, b]) \subset [f (\underline{x}), f (\bar{x})]

Otherwise the intermediate value theorem [6.6.2] guarantees that every number in $[f (\underline{x}), f (\bar{x})]$ is a value for f, i.e. we have additionally

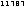f ([a, b]) \supset [f (\underline{x}), f (\bar{x})]

6.5. 6.7.