6.5. Uniformly Continuous Functions

In this part we introduce an alternative notation of continuity, the so called

ε / δ

-notation. It no longer needs sequences to be involved which in fact offers the option to introduce other concepts of continuity.

Proposition: For any function $f : A \to ℝ$ and any $a \in A$ we have:

f continuous at a $\Leftrightarrow$	For each $ε > 0$ there is a $δ > 0$ such that every $x \in A$ satisfies
	$\| x - a \| < δ \Rightarrow \| f (x) - f (a) \| < ε$	[6.5.1]

Proof:
" $\Rightarrow$ ": Suppose that for a single $ε > 0$ there is no $δ$ of the required kind. In particular we will find an $a_{n} \in A$ for each $n \in ℕ^{*}$ such that $| a_{n} - a | < \frac{1}{n}$ but $| f (a_{n}) - f (a) | \geq ε$ . Thus we have got a sequence $(a_{n})$ in A, converging to a, with $f (a)$ not being the limit of its image sequence $(f (a_{n}))$ . Contradiction!

" $\Leftarrow$ ": Now let $(a_{n})$ be a sequence in A converging to a. We have to show: $f (a_{n}) \to f (a)$ . So let $ε > 0$ be arbitrary. From the premise we get a $δ > 0$ such that the implication

| x - a | < δ \Rightarrow | f (x) - f (a) | < ε

[0]

is valid for all $x \in A$ . As $a_{n} \to a$ we have $| a_{n} - a | < δ$ for all n from a suitable $n_{0}$ onwards. Acoording to [0] these n satisfy:

| f (a_{n}) - f (a) | < ε

Consider:

The criterion in the $ε / δ$ -notation can be restated like this: For each $ε > 0$ there is a $δ > 0$ such that

$x \in A \cap] a - δ, a + δ [\Rightarrow f (x) \in] f (a) - ε, f (a) + ε [$

In other words: For every relative $ε$ -neighbourhood $ℝ_{f (a), ε}$ there is a relative $δ$ -neighbourhood $A_{a, δ}$ with

$f (A_{a, δ}) \subset ℝ_{f (a), ε}$

Functions are often continuous at many points of their domain. It should be emphasized that the interaction guaranteed by the $ε / δ$ -notation between a given $ε$ and a suitable $δ$ normally depends on the focussed point a and it is very unlikely that $δ$ could be set uniformly for all a. The following notion thus establishes another, narrower concept of continuity.

Definition: A function $f : B \to ℝ$ is called uniformly continuous on $A \subset B$ if there is a $δ > 0$ for each $ε > 0$ such that

| x - y | < δ \Rightarrow | f (x) - f (y) | < ε for all x, y \in A

[6.5.2]

Consider: This new notion of continuity is a special version of the old one, because:

Proposition:

If f is uniformly continuous on A then f is continuous at every $a \in A$ .

[6.5.3]

The continuous function $\frac{1}{X}$ fails to be uniformly continuous on $ℝ^{> 0}$ .

[6.5.4]

Proof:

1. ► Specialising $y = a$ in [6.5.2] immediately yields [6.5.1].

2. ► Suppose the reciprocal function would be uniformly continuous. Then there is a $δ > 0$ for $ε = 1$ such that all $x, y > 0$ satisfy

| x - y | < δ \Rightarrow | \frac{y - x}{x y} | = | \frac{1}{x} - \frac{1}{y} | < 1

We may assume $δ < \frac{1}{2}$ . Choosing a positive $x < \frac{δ}{2}$ and setting $y ≔ x + \frac{δ}{2}$ leads to the contradiction

1 > | \frac{x + \frac{δ}{2} - x}{x (x + \frac{δ}{2})} | = \frac{\frac{δ}{2}}{x (x + \frac{δ}{2})} > \frac{\frac{δ}{2}}{\frac{δ}{2} (\frac{δ}{2} + \frac{δ}{2})} = \frac{1}{δ} > 2

In [6.5.4] we used the reciprocal function to show that [6.5.3] is not reversible. Surprisingly there are no counter examples among the functions on a closed interval. The following theorem is a valuable resource when it comes to estimates.

Theorem: Continuous functions on closed intervals are uniformly continuous:

f \in C^{0} ([a, b]) \Rightarrow

f is uniformly continuous on

[a, b]

[6.5.5]

Proof: Let $ε > 0$ be given. We proceed indirectly and suppose there would be no $δ$ of the required kind, more than ever none of the type $\frac{1}{n}$ . Then for each $n \in ℕ^{*}$ we have numbers $x_{n}, y_{n} \in [a, b]$ such that

| x_{n} - y_{n} | < \frac{1}{n} \land | f (x_{n}) - f (y_{n}) | \geq ε

[1]

$(x_{n})$ is a bounded sequence and thus has an accumulation point $x^{*}$ (cf. Bolzano-Weierstrass theorem [5.8.6]). According to [5.8.5] $x^{*}$ is the limit of a suitable subsequence of $(x_{n})$ and thus a member of $[a, b]$ .

As f is continuous at $x^{*}$ there is a $δ > 0$ such that all $x \in [a, b]$ meet the implication

| x - x^{*} | < δ \Rightarrow | f (x) - f (x^{*}) | < \frac{ε}{2}

[2]

The neighbourhood $] x^{*} - \frac{δ}{2}, x^{*} + \frac{δ}{2} [$ contains infinitely many members of $(x_{n})$ (since $x^{*}$ is an accumulation point). Among them there will be definitely one with an index n satisfying $\frac{1}{n} < \frac{δ}{2}$ . Using [1] we now estimate for this n:

| y_{n} - x^{*} | \leq | y_{n} - x_{n} | + | x_{n} - x^{*} | < \frac{δ}{2} + \frac{δ}{2} = δ

and thus get (with [2])

| f (x_{n}) - f (y_{n}) | \leq | f (x_{n}) - f (x^{*}) | + | f (x^{*}) - f (y_{n}) | < \frac{ε}{2} + \frac{ε}{2} = ε

which contradicts [1].

As seen in [6.5.4] the interval needs to be closed for this theorem to be valid. The next part will show that continuous functions on closed intervals indeed excel in very special properties.

We end this part with a special variant of uniform continuity, the so called lipschitz-continuity:

Definition: A function $f : B \to ℝ$ is called lipschitz-continuous on $A \subset B$ if there is a $c > 0$ such that

| f (x) - f (y) | < c \cdot | x - y | for all x, y \in A

[6.5.6]

Consider:

Lipschitz-continuous functions are uniformly continuous: For each $ε > 0$ the fraction $\frac{ε}{c}$ is a suitable $δ$ .
The reverse is generally not true. The root function as an example is uniformly continuous on $[0, 1]$ according to [6.5.5], but fails to be lipschitz-continuous.

If there would be a $c > 0$ holding the estimate $| \sqrt{x} - \sqrt{y} | < c \cdot | x - y |$ for all $x, y \in [0, 1]$ we could specialise $x = \frac{1}{n}$ and $y = 0$ to get

$\sqrt{\frac{1}{n}} < c \cdot \frac{1}{n}$

Choosing now an $n > c^{2}$ , i.e $c < \sqrt{n}$ , will yield the contradiction $\sqrt{\frac{1}{n}} < c \cdot \frac{1}{n} < \frac{\sqrt{n}}{n} = \sqrt{\frac{1}{n}}$ .

Of special interest are lipschitz-continuous functions with a lipschitz continuity constant c below 1. Because in that case the distance of two values of f is less than the distance of their invers images and with functions that map closed intervals onto themselves this will lead to a fixed point.

Theorem (Banach fixed point theorem): If a function $f : [a, b] \to [a, b]$ allows a number $c \in] 0,1 [$ such that

| f (x) - f (y) | < c \cdot | x - y | for all x, y \in [a, b]

then there is an $\tilde{x} \in [a, b]$ satisfying

f (\tilde{x}) = \tilde{x}

[6.5.7]

Proof: For our constructive approach we introduce the recursion

a_{1} ≔ a \land a_{n + 1} ≔ f (a_{n})

Due to the premise the estimate $| a_{n + 1} - a_{n + 2} | = | f (a_{n}) - f (a_{n + 1}) | < c \cdot | a_{n} - a_{n + 1} |$ holds for each $n \in ℕ^{*}$ and is extendable by induction to

| a_{n + 1} - a_{n + 2} | < c^{n} \cdot | a_{1} - a_{2} |

If $m > n + 1$ we can use the summation formula for the geometric series (c.f. [5.2.4]) to estimate as follows:

\begin{array}{l} | a_{n + 1} - a_{m} | & = | a_{n + 1} - a_{n + 2} + a_{n + 2} - a_{n + 3} + \dots + a_{m - 1} - a_{m} | \\ \leq | a_{n + 1} - a_{n + 2} | + | a_{n + 2} - a_{n + 3} | + \dots + | a_{m - 1} - a_{m} | \\ \leq c^{n} \cdot | a_{1} - a_{2} | + c^{n + 1} \cdot | a_{1} - a_{2} | + \dots + c^{m - 2} \cdot | a_{1} - a_{2} | \\ = c^{n} \cdot | a_{1} - a_{2} | \cdot (c^{0} + c^{1} + \dots + c^{m - n - 2}) \\ = c^{n} \cdot | a_{1} - a_{2} | \cdot \frac{1 - c^{m - n - 1}}{1 - c} \\ \leq c^{n} \cdot | a_{1} - a_{2} | \cdot \frac{1}{1 - c} \end{array}

With $| c | < 1$ the sequence $(c^{n})$ proves to be a zero sequence (c.f. [5.7.2]). So from the estimate above we conclude that $(a_{n})$ is a Cauchy sequence and thus is convergent (in $ℝ$ ) with a limit $\tilde{x}$ . At first we see that $\tilde{x} \in [a, b]$ and then, as f is continuous at $\tilde{x}$ , we have:

f (\tilde{x}) = f (lim a_{n}) = lim f (a_{n}) = lim a_{n + 1} = \tilde{x}

Consider:

The fixed point $\tilde{x}$ in [6.5.7] is uniquely determined. If $\bar{x} \neq \tilde{x}$ would be a further fixed point in $[a, b]$ the calculation

$| \bar{x} - \tilde{x} | = | f (\bar{x}) - f (\tilde{x}) | < c \cdot | \bar{x} - \tilde{x} |$

implies the contradiction $1 < c$ .
The Banach fixed point theorem provides an elegant way to introduce square roots in $ℝ$ . Take e.g. $a > 1$ . For $x \in [1, a]$ we have in this case

$1 = \frac{1}{2} (1 + \frac{a}{a}) \leq \frac{1}{2} (x + \frac{a}{x}) \leq \frac{1}{2} (a + \frac{a}{1}) = a$

so that $f (x) ≔ \frac{1}{2} (x + \frac{a}{x})$ defines a function $f : [1, a] \to [1, a]$ . f is lipschitz-continuous with $c = \frac{1}{2}$ :

$\begin{array}{l} | f (x) - f (y) | & = \frac{1}{2} | x - y + \frac{a}{x} - \frac{a}{y} | \\ = \frac{1}{2} | x - y + \frac{a y - a x}{x y} | \\ = \frac{1}{2} | x - y | \cdot | 1 - \frac{a}{x y} | \\ < \frac{1}{2} | x - y | \end{array}$

Thus f has a unique fixed point $\tilde{x}$ which in fact means there is a unique positive number in $[1, a]$ with its square equal to a:

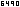$\begin{array}{l} x = \frac{1}{2} (x + \frac{a}{x}) \\ \Leftrightarrow & 2 x^{2} = x^{2} + a \\ \Leftrightarrow & x^{2} = a \end{array}$

6.4. 6.6.