Example of a locally non-injective, regular function

Consider the function  ${\displaystyle f:ℝ\to ℝ}$ where ${\displaystyle f(x)≔\{\begin{array}{l}x+x^2\cos \frac{\mathrm{\pi }}{x}\text{ , if }x\ne 0\hfill \\ 0\text{ , if }x=0\hfill \end{array}}$

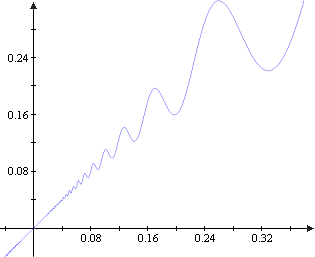
f is a sample function of the required kind, as we will show:

1. f is differentiable at 0 and  ${\displaystyle f^{\prime }(0)=1}$.

2. f fails to be one-to-one in every neighbourhood of 0.

Proof:  

1. ►  The inequality

is obviously valid for all ${\displaystyle x\ne 0}$ so that the nesting theorem [6.9.10] yields ${\displaystyle \underset{x\to 0}{\lim }|m_0(x)-1|=0}$. According to [6.9.11] this is the assertion ${\displaystyle \underset{x\to 0}{\lim }{m}_0(x)=1}$.

2. ►  f is continuous (at 0 due to 1. and for ${\displaystyle x\ne 0}$ due to the calculation rules for continuous functions). Now for an arbitrary ${\displaystyle k\in {\mathbb{N}}^{\ast }}$ we consider the numbers

They will satisfy

This assumed the intermediate value theorem ([6.6.2]) will provide an ${\displaystyle \tilde{x}\in ]\frac{1}{2k+1},\frac{1}{2k}[}$, in particular ${\displaystyle \tilde{x}\ne \frac{1}{2k+2}}$, such that  ${\displaystyle f(\tilde{x})=f(\frac{1}{2k+2})}$. But this proves that  f is not injective on ${\displaystyle ]-\frac{1}{2k},\frac{1}{2k}[}$.

To validate [1] and [2] note that the cosine takes the value 1 for all even multiples of π, and the value −1 for all the odd ones. So we have

[1] is thus valid due to the following calculation:

For [2] we find a similar calculation: