4.7. Umkehrbare Funktionen

Im Zusammenhang mit der Hintereinanderausführung studiert man auch das Problem der Umkehrbarkeit von Funktionen. Dahinter verbirgt sich die folgende Fragestellung: Ist

f : A \to B

irgendeine Funktion, so ist f eine Teilmenge von

A \times B

, die bestimmte Bedingungen erfüllt. Wenn man nun f "umkehrt", d.h. bei den Paaren, die f ausmachen, die Koordinaten vertauscht, also übergeht zur Teilmenge

f^{- 1} ≔ {(y, x) | (x, y) \in f} \subset B \times A

, ist dann damit automatisch eine neue Funktion von B nach A gegeben oder nicht?

Nach den bisherigen Erfahrungen sind die Aussichten dafür eher gering; so ist etwa für die konstante Funktion 2 auf $ℝ$ , also für die Teilmenge $2 = {(x,2) | x \in ℝ}$ ,

2^{- 1} = {(y, x) | (x, y) \in 2} = {(2, x) | x \in ℝ}

und hier wird außer der 2 keinem Element etwas zugeordnet und der 2 überdies auch noch unendlich viele!

Ist jedoch die Ausgangsfunktion f "gut genug", so ist auch ihre Umkehrung wieder eine Funktion:

Definition und Bemerkung: Wir nennen eine Funktion $f : A \to B$ umkehrbar (oder bijektiv), falls jedes Element $y \in B$ genau ein Urbild $x \in A$ besitzt. In diesem Fall stellt die Menge

f^{- 1} ≔ {(y, x) | (x, y) \in f} \subset B \times A

[4.7.1]

eine Funktion von B nach A dar. Sie ordnet jedem $y \in B$ das einzige Urbild $x \in A$ zu.

Ist f bijektiv, so nennen wir $f^{- 1}$ eine Umkehrfunktion von f.

Wir benutzen hier dasselbe Symbol wie bei einer Potenzfunktion mit Exponent −1. Aus dem Kontext geht aber immer hervor, welche Bedeutung gerade gemeint ist.

Wir beginnen unsere Untersuchungen zur Umkehrbarkeit von Funktionen mit der Rolle der leeren Funktion und fragen:

Kann die Funktion

\emptyset : A \to B

überhaupt umkehrbar sein?

Ist $A \neq \emptyset$ , so liegt überhaupt keine Funktion vor; ist $B \neq \emptyset$ , so hat kein y aus B ein Urbild. Man hat also:

\emptyset : A \to B

ist umkehrbar

\Leftrightarrow A = \emptyset \land B = \emptyset

In diesem Fall ist $\emptyset^{- 1} = \emptyset$ und $X_{A} = X_{B} = \emptyset$ . Alle folgenden Bemerkungen sind auch für die leere Funktion gültig; der Beweis ergibt sich dabei stets aus den gerade genannten Beziehungen. Die im Weiteren notierten Beweise berücksichtigen nur den nicht-leeren Fall.

Die Formulierung eine Umkehrfunktion in [4.7.1] ist unnötig vorsichtig: Bijektive Funktionen haben genau eine Umkehrfunktion.

Definition: Ist $f : A \to B$ umkehrbar, so heben sich $f$ und $f^{- 1}$ in ihrer Wirkung gegenseitig auf:

f^{- 1} \circ f = X_{A} \land f \circ f^{- 1} = X_{B}

[4.7.2]

Diese Eigenschaft charakterisiert darüber hinaus die Umkehrbarkeit bereits vollständig. Ist nämlich $g : B \to A$ eine Funktion, derart dass

g \circ f = X_{A} \land f \circ g = X_{B}

,[*]

so ist f umkehrbar und $g = f^{- 1}$ . Insbesondere ist damit $f^{- 1}$ die einzige Funktion, die [*] erfüllt; wir nennen sie daher die Umkehrfunktion zu f .

Beweis: Wir zeigen zunächst die beiden Eigenschaften von $f^{- 1}$ :

$f^{- 1} \circ f : {x \in A | f (x) \in B} = A \to A$ und für alle $x \in A$ ist
$f^{- 1} \circ f (x) = f^{- 1} (f (x)) = x$ , denn x ist das einzige Urbild von $f (x)$ .
$f \circ f^{- 1} : {x \in B | f^{- 1} (x) \in A} = B \to B$ und für alle $x \in B$ hat man:
$f \circ f^{- 1} (x) = f (f^{- 1} (x)) = x$ , denn $f^{- 1} (x)$ ist nach Definition ein Urbild von x.

Sei nun $g : B \to A$ mit genannten Eigenschaften gegeben. Wir zeigen die Umkehrbarkeit von f und geben dazu ein $y \in B$ vor. Da $f \circ g = X_{B}$ hat man: $y = X_{B} (y) = f (g (y))$ , d.h. y ist das f-Bild von $g (y) \in A$ . Also hat y überhaupt ein Urbild. Hätte y nun zwei Urbilder, etwa $x_{1}, x_{2} \in A$ , so wäre

\begin{array}{l} f (x_{1}) = y = f (x_{2}) \\ \Rightarrow & x_{1} = g \circ f (x_{1}) = g (y) = g \circ f (x_{2}) = x_{2} . \end{array}

Daher hat y auch nur ein Urbild, d.h. f ist umkehrbar. Schließlich ist $g = f^{- 1}$ , denn:

g = g \circ X_{B} = g \circ (f \circ f^{- 1}) = (g \circ f) \circ f^{- 1} = X_{A} \circ f^{- 1} = f^{- 1}

In konkreten Fällen benötigen wir geeignete Verfahren, um Umkehrfunktionen zu finden. Kann man f graphisch darstellen, so lässt sich auch die Teilmenge $f^{- 1}$ , also die Menge ${(y, x) | (x, y) \in f}$ , überblicken, denn sie entsteht aus f durch Vertauschen der Koordinaten, so dass ihr Bild durch Spiegeln an der 1. Winkelhalbierenden gewonnen werden kann.

Spiegelt man z.B. den Graphen der Funktion $2 X + 3$ , so sieht das Spiegelbild durchaus wie ein Funktionsgraph aus; $2 X + 3$ ist also wahrscheinlich umkehrbar.

Eine Berechnung der Umkehrfunktion ersetzt dieses Grafik natürlich nicht. Hierzu benutzt man meist die folgende Überlegung:

Bemerkung: Eine Funktion $f : A \to B$ ist genau dann umkehrbar, wenn sich für jedes $y \in B$ die Gleichung

f (x) = y

[4.7.3]

eindeutig nach x auflösen lässt. In diesem Fall stellt die Zuordnung $y \mapsto x$ die Umkehrfunktion dar.

Beweis: Es ist eigentlich nichts zu zeigen, denn die eindeutige Lösbarbarkeit der Gleichung bedeutet nichts anderes, als dass jedes y genau ein Urbild hat.

Wir demonstrieren dieses Prinzip an unserem Eingangsbeispiel $2 X + 3$ : Für ein beliebiges $y \in ℝ$ hat man:

2 X + 3 (x) = y \Leftrightarrow 2 x + 3 = y \Leftrightarrow x = \frac{1}{2} (y - 3)

Also ist $2 X + 3$ umkehrbar und die Zuordnung $y \mapsto \frac{1}{2} (y - 3)$ liefert $\frac{1}{2} (X - 3)$ als Umkehrfunktion.

Mit Hilfe des gerade beschriebenen Verfahrens gelingt es, die konstanten und die linearen Funktionen auf $ℝ$ vollständig zu überblicken.

Bemerkung:

Keine konstante Funktion $c : ℝ \to ℝ$ ist umkehrbar.	[4.7.4]
Jede lineare Funktion $m X + b : ℝ \to ℝ$ , mit $m \neq 0$ ist umkehrbar. Die Umkehrfunktion ist wieder linear; ihre Steigungszahl ist der Kehrwert der alten: $\frac{1}{m}$ .	[4.7.5]

Beweis:

1. ► $c + 1$ etwa hat kein Urbild.

2. ► Für jedes $y \in ℝ$ ist

m X + b (x) = y \Leftrightarrow m x + b = y \Leftrightarrow x = \frac{y - b}{m}

Daher ist $m X + b$ umkehrbar und $\frac{1}{m} X - \frac{b}{m}$ die Umkehrfunktion.

Bei der Umkehrbarkeit von Funktionen spielen Definitions- und Bildbereich eine entscheidendere Rolle als bisher. Dies zeigt sich sehr deutlich am Beispiel der Quadratfunktion.

Beispiel:

Die Quadratfunktion $X^{2} : ℝ \to ℝ$ ist nicht umkehrbar.	[4.7.6]
Die Funktion $f : ℝ \to ℝ^{\geq 0}$ ist nicht umkehrbar.	[4.7.7]
Die Funktion $f : ℝ^{\geq 0} \to ℝ^{\geq 0}$ gegeben durch $f (x) = x^{2}$ ist umkehrbar. Ihre Umkehrfunktion ist nicht die Wurzelfunktion $\sqrt{X} : ℝ^{\geq 0} \to ℝ$ , sondern die Funktion $g : ℝ^{\geq 0} \to ℝ^{\geq 0}$ gegeben durch $g (x) = \sqrt{x}$ .	[4.7.8]

Beweis:

1. ► $- 1$ z.B. hat kein Urbild.

2. ► 4 etwa hat zwei Urbilder: 2 und −2.

3. ► Für $x, y \in ℝ^{\geq 0}$ hat man:

f (x) = y \Leftrightarrow x^{2} = y \Leftrightarrow x = \sqrt{y}

Bei den trigonometrischen Funktionen auf $ℝ$ führen Überlegungen zur Umkehrbarkeit zu neuen Funktionen. Ohne Beweis notieren wir hier das folgende Ergebnis:

Bemerkung:

sin und cos sind nicht umkehrbar, denn z.B. hat 0 in beiden Fällen unendlich viele Urbilder.

[4.7.9]

Durch Reduktion auf geeignete Definitions- und Bildbereiche gelingt es, Einschränkungen dieser Funktionen umzukehren. Genauer gilt: Die Funktion

$\sin | [- \frac{π}{2}, \frac{π}{2}] : [- \frac{π}{2}, \frac{π}{2}] \to [- 1,1]$ ist umkehrbar. Die Umkehrfunktion ist der Arcussinus
$\arcsin : [- 1,1] \to [- \frac{π}{2}, \frac{π}{2}]$ .
$\cos | [0, π] : [0, π] \to [- 1,1]$ ist umkehrbar. Die Umkehrfunktion ist der Arcuscosinus
$\arccos : [- 1,1] \to [0, π]$ .
$\tan | [- \frac{π}{2}, \frac{π}{2}] : [- \frac{π}{2}, \frac{π}{2}] \to ℝ$ ist umkehrbar. Die Umkehrfunktion ist der Arcustangens
$\arctan : ℝ \to [- \frac{π}{2}, \frac{π}{2}]$ .
$\cot | [0, π] : [0, π] \to ℝ$ ist umkehrbar. Die Umkehrfunktion ist der Arcuscotangens
$arccot : ℝ \to [0, π]$ .

[4.7.10]

Das Kriterium [*] aus [4.7.2] ist oft die einzige Möglichkeit, theoretische Ergebnisse zu gewinnen. Die folgende Bemerkung zeigt, dass die bijektiven Funktionen eine algebraische Struktur besitzen.

Bemerkung: Für beliebige, nicht-leere Mengen A, B und C gilt:

$X_{A}$ ist umkehrbar und $X_{A}^{- 1} = X_{A}$ .	[4.7.11]
Mit $f : A \to B$ ist auch $f^{- 1}$ umkehrbar. Dabei ist $(f^{- 1})^{- 1} = f$ .	[4.7.12]
Sind $g : A \to B$ und $f : B \to C$ umkehrbar, so ist auch $f \circ g$ umkehrbar und ${(f \circ g)}^{- 1} = g^{- 1} \circ f^{- 1}$ .	[4.7.13]

Da $\circ$ assoziativ, aber nicht kommutativ ist, hat man mit [4.7.11/12/13] für die Menge $B (A)$ aller bijektiven Funktionen von A nach A:

(B (A), \circ)

ist eine eine nicht-abelsche Gruppe.

Dabei ist $X_{A}$ das neutrale und $f^{- 1}$ das zu f inverse Element.

Beweis: In allen drei Fällen reicht es zu zeigen, dass die jeweils anstehende Funktion das Kriterium [*] in [4.7.2] erfüllt, also dort die Rolle von g übernimmt.

1. ► Hier sind beide Gleichungen identisch und trivialerweise gültig: $X_{A} \circ X_{A} = X_{A}$ .

2. ► Man hat für die Umkehrfunktion $f^{- 1}$ :

f^{- 1} \circ f = X_{A}

und

f \circ f^{- 1} = X_{A}

Damit aber erfüllt f (in vertauschter Reihenfolge) genau die definierenden Gleichungen für $(f^{- 1})^{- 1}$ .

3. ► Wir rechnen nach, dass $g^{- 1} \circ f^{- 1}$ [*] erfüllt. Da $\circ$ assoziativ ist hat man:

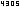\begin{array}{l} (g^{- 1} \circ f^{- 1}) \circ (f \circ g) = g^{- 1} \circ ((f^{- 1} \circ f) \circ g) = g^{- 1} \circ (X_{A} \circ g) = g^{- 1} \circ g = X_{A} \\ (f \circ g) \circ (g^{- 1} \circ f^{- 1}) = f \circ ((g \circ g^{- 1}) \circ f^{- 1}) = f \circ (X_{A} \circ f^{- 1}) = f \circ f^{- 1} = X_{A} \end{array}

4.6. 4.8.