4.8. Gleichmächtige Mengen
Bijektive Funktionen spielen in der Mengenlehre eine ungemein wichtige Rolle. Mit ihnen kann man u.a. präzise beschreiben, wann zwei Mengen gleich viele
Elemente enthalten, so dass schließlich die Mengen hinsichtlich ihrer Elementanzahl klassifiziert werden können.
|
Definition: Zwei Mengen M und N heißen gleichmächtig (in Zeichen ), falls es eine bijektive Funktion
|
[4.8.1] |
gibt
|
ist eine Äquivalenzrelation. Das zeigt (u.a.) die folgende Bemerkung.
|
Bemerkung:
-
|
[4.8.2] |
-
|
[4.8.3] |
-
|
[4.8.4] |
-
|
[4.8.5] |
Beweis:
1. ► Ist , so gibt es eine bijektive Funktion von . Falls , gibt es aber überhaupt keine Funktion von . Ist , so ergibt sich die Behauptung aus 2.
2. ► ist eine umkehrbare Funktion von ([4.7.11]).
3. ► Ist bijektiv, so ist ebenfalls bijektiv ([4.7.12]).
4. ► Sind und bijektiv, so ist auch bijektiv ([4.7.13]).
|
Das Konzept der Gleichmächtigkeit ist ein unentbehrliches Hilfsmittel bei der Untersuchung unendlicher Mengen. Einige Mengentypen zeichnen wir durch einen Namen aus:
|
Definition:
-
Eine Menge M heißt endlich falls oder falls es ein gibt, so dass .
|
[4.8.6] |
-
Eine Menge M heißt abzählbar falls . Jede Bijektion heißt eine Abzählung von M.
|
[4.8.7] |
-
Eine Menge M heißt unendlich falls M nicht endlich ist.
|
[4.8.8] |
-
Unendliche Mengen, die nicht abzälbar sind, nennen wir überabzählbar.
|
[4.8.9] |
|
In der nächste Bemerkung notieren wir zunächst drei elementare Aussagen. Sie strapazieren die Anschauung nicht. Die Aussage 4, keine Menge ist gleichmächtig zu ihrer Potenzmenge
 , ,
i   |
|
Die Potenzmenge von M ist die Menge aller Teilmengen von M:
|
ist dagegen wesentlich anspruchsvoller, denn da wir über die Zuordnung M als Teilmenge von auffassen dürfen, bedeutet 4: Jede Menge lässt sich eine mächtigere Menge einbetten. Dies begründet einen schier unüberblickbaren "Mächtigkeitenzoo" überabzählbarer Mengen.
|
Bemerkung:
-
Jede Menge der Form , ist endlich.
|
[4.8.10] |
-
Jede abzählbare Menge M ist unendlich.
|
[4.8.11] |
-
ist nicht abzählbar.
|
[4.8.12] |
-
|
[4.8.13] |
Beweis:
1. ► Offensichtlich ist eine bijektive Funktion von .
2. ► Sei eine Abzählung von M. Insbesondere ist damit . Wäre nun M endlich, so gäbe es für ein eine Bijektion . ist dann aber eine umkehrbare Funktion von . Dabei kann h gar nicht bijektiv sein, denn es gibt natürliche Zahlen ohne h-Urbild, z.B. die Zahl - Widerspruch!
3. ► Ergibt sich sofort aus 2.
4. ► Der sehr elegante Beweis geht auf Cantor zurück. Wir müssen zeigen: keine Funktion ist umkehrbar. Angenommen, es gibt eine solche Funktion f. Wir betrachten dann die Menge
.
A kann aber kein Urbild besitzen, denn die Gleichung für ein erzeugt den Widerspruch
,
f ist also nicht bijektiv - Widerspruch!
|
Wir ermitteln nun die Unendlichkeitssorten der klassischen Zahlenmengen. Ohne große Mühe gelingt dies bei und bei .
|
Bemerkung:
-
ist abzählbar.
|
[4.8.14] |
-
ist abzählbar.
|
[4.8.15] |
Beweis:
1. ► ist eine Bijektion von .
2. ► Die Aufgabe besteht darin, die Elemente von , d.h. die Zahlen .....,−2,−1,0,1,2,..... mit natürlichen Zahlen durchzunummerieren. Dies scheint schwierig zu sein, da keinen "Anfang" hat; die folgende Umsortierung aber räumt dieses Hindernis aus dem Weg: 0,−1,1,−2,2,...... Mit Hilfe der Gaußfunktion

i   |
|
Die Gauß- oder floor-Funktion haben wir in [4.2.15] eingeführt:
.
|
können wir diese Nummerierung durch eine Funktion erzeugen:
gegeben durch
ist bijektiv und mit
ist die Umkehrfunktion.
Zum Beweis reicht es nach [4.7.2] zu zeigen, dass sich f und g in ihrer Wirkung gegenseitig aufheben:
-
Für ist .
-
Für ist .
-
Ist gerade, etwa , so ist .
-
Ist ungerade, etwa , so ist .
|
Mit der folgende Bemerkung verschaffen wir uns einen Überblick über die Teilmengen von und ihre Mächtigkeiten. Entscheiden für die Beweise ist dabei das Induktionsaxiom [5.2.1]:
Jede nicht-leere Teilemenge A von besitzt ein kleinstes Element .
|
Bemerkung:
-
Sei . Jede Teilmenge A von ist endlich.
|
[4.8.16] |
-
Jede Teilmenge A von ist höchstens abzählbar, d.h. endlich oder abzählbar.
|
[4.8.17] |
Beweis:
1. ► Falls , ist nichts zu zeigen. Sei also . Wir bilden A nun bijektiv auf einen fortlaufenden Abschnitt ab, wobei wir zunächst die Länge k dieses Abschnitts benötigen. Dazu "zählen" wir die Elemente von A mit Hilfe ihrer Indikatorfunktion

i   |
|
Die Indikatorfunktion (auch charakteristische Funktion) einer Menge A, haben wir in [4.2.15] eingeführt:
|
und setzen
.
Da , ist . Für z.B. ist
.
Auf ähnliche Weise definieren wir nun die Funktion durch
.
Da , besitzt A ein kleinstes Element , wobei offensichtlich ist. Ferner hat man
,
d.h. entsteht aus durch Addition von 1 oder 0, also ist insbesondere . Außerdem ist , also sind alle Werte von g natürliche Zahlen zwischen 1 und k, liegen daher im angegebenen Bildbereich.
Wir zeigen jetzt die Bijektivität von g:
-
Verschiedene Elemente aus A haben verschiedene Bilder (also besitzt jedes Bild auch höchstens ein Urbild):
Sind i und j zwei verschiedene Elemente aus A, etwa , so ist
.
-
Jedes hat mindestens ein Urbild:
Sei anderenfalls j das kleinste Element von ohne Urbild. Da 1 ein Urbild hat, nämlich , ist und hat ein Urbild in A, etwa . Wäre , so wäre
.
Daher ist die Restmenge und für ihr kleinstes Element hat man:
.
j hat also ein Urbild, nämlich s - Widerspruch!
Mit g ist auch die Funktion h gegeben durch eine Bijektion, und zwar von . ist somit endlich.
2. ► Sei A eine nicht-endliche Teilmenge von . Zunächst bilden wir A bijektiv auf ab und bemühen dazu noch einmal die Indikatorfunktion . Für gegeben durch
zeigt man genau wie gerade: jedes hat höchstens ein Urbild. g ist also bijektiv, wenn wir nachweisen können, dass jedes auch mindestens ein Urbild hat. Auch hier gehen wir i.w. wie in Punkt 1 vor.
Zunächst hat 1 ein Urbild, denn als nicht-endliche, also auch nicht-leere Menge besitzt A ein Minimum, also: . Sei jetzt angenommen, es gibt ein ohne Urbild. O.E. sei j das kleinste Element dieser Art, dann ist und besitzt ein Urbild, etwa .
Wäre nun , so wäre A nach [4.8.16] endlich. Also ist wieder und ein Urbild zu j. - Widerspruch.
Die Umkehrbarkeit von g garantiert nun, dass auch gegeben durch
bijektiv ist. A ist damit abzählbar.
|
[4.8.16/17] lassen sich leicht auf beliebige Mengen übertragen.
|
Bemerkung:
-
Ist M endlich, so ist jede Teilmenge A von M endlich.
|
[4.8.18] |
-
Ist M abzählbar, so ist jede Teilmenge A von M höchstens abzählbar.
|
[4.8.19] |
Beweis:
1. ► Für ist nichts zu zeigen. Ist A nicht-leer, so ist auch M nicht-leer. Gemäß Voraussetzung gibt es ein und eine Bijektion . Nach [4.8.16] ist eine endliche Teilmenge von , es gibt daher für ein geeignetes eine Bijektion . Dann ist aber eine umkehrbare Funktion von , also endlich.
2. ► Wir betrachten o.E. nur den Fall . Sei eine Abzählung von M. Nach [4.8.17] ist eine (nicht-leere) endliche oder eine abzählbare Teilmenge von .
Im ersten Fall gibt es eine Bijektion . Die bijektive Funktion belegt dann die Endlichkeit von A.
Im zweiten Fall existiert eine Bijektion . belegt hier, dass A abzählbar ist.
|
Ein wichtiges Ergebnis in der Mengenlehre garantiert, dass abzählbare Vereinigungen abzählbarer Mengen wieder abzählbar sind. Wir beweisen hier eine abgeschwächte Variante, mit der wir die noch ausstehenden Mächtigkeiten von und leichter ermitteln können.
|
Bemerkung: Für jedes sei eine endliche, nicht-leere Menge. Sind die Mengen paarweise disjunkt, so ist die Menge
|
[4.8.20] |
abzählbar.
Beweis: Zunächst gibt es nach Voraussetzung zu jedem ein und eine Bijektion
.
Setzen wir für ein , also für genau ein i
,

i   |
|
Für existiert der Ausdruck nicht. Wir setzen in diesem Fall:
und
.
|
so ist die dadurch gegebene Funktion umkehrbar. Die Umkehrfunktion ist die Funktion , gegeben durch
[+], wobei
.
erfüllt nach Konstruktion die folgenden Abschätzungen:
wobei [++] gewährleistet. [+] ist also wohldefiniert.
Zum Beweis zeigen wir wieder, dass sich f und g in ihrer Wirkung gegenseitig aufheben:
- Für ein hat man:
-
Sei nun , etwa . Da hat man zunächst
,
womit gezeigt ist, dass das zu gehörige identisch mit i ist. Damit gilt jetzt:
|
Mit [4.8.20] hat man eine alternative, bequemere Möglichkeit, die Abzählbarkeit von nachzuweisen: Die abzählbar vielen Mengen
sind nämlich endlich, nicht-leer, paarweise disjunkt und es ist .
Wir wenden uns nun der Menge der rationalen Zahlen zu.
|
Bemerkung:
ist abzählbar.
|
[4.8.21] |
Beweis: Wir zerlegen in abzählbar viele endliche Mengen. Bei der Darstellung von Brüchen darf man o.E. annehmen, dass alle Nenner positiv sind und nur maximal gekürzte Bruchdarstellungen vorkommen, also:
.
Wenn wir für den Augenblick den Bruch als Zahlenpaar schreiben,  haben wir die Möglichkeit, ihn als Gitterpunkt der Zeichenebene zu sehen.
haben wir die Möglichkeit, ihn als Gitterpunkt der Zeichenebene zu sehen.
So sind etwa die auf den roten Diagonalen liegenden Brüche durch die Paare (−4,1), (−3,2), (−2,3), (−1,4), (0,5), (1,4), (2,3), (3,2) und (4,1) gegeben.
Addiert man nun bei diesen Paaren die Beträge der Koordinaten, also z.B. , so erhält man in allen Fällen den Wert 5! (Die genannten neun Paare sind übrigens die einzigen, die auf diese Weise den Wert 5 liefern.)
Für eine Bruchzahl setzen wir jetzt
.
Da wir nur maximal gekürzte Darstellungen zulassen, gehört zu jeder rationalen Zahl x genau eine Zahl . Außerdem haben nur endlich viele Zahlen x denselben Wert .
Die Mengen , sind daher endlich, nicht-leer und paarweise disjunkt. Ihre Vereinigung ist . Nach dem Satz über abzählbare Vereinigungen ist somit abzählbar.
Die Zerlegungsmengen enthalten offensichtlich genau diejenigen teilerfremden Brüche, die auf dem i-ten Diagonalenpaar liegen. Diese Art der Aufteilung heißt Cantorsches Diagonalverfahren.
|
Mit unserer letzten Zahlenmenge, der Menge der reellen Zahlen verlassen wir die Klasse der abzählbaren Mengen.
|
Bemerkung:
ist überabzählbar.
|
[4.8.22] |
Beweis: Es reicht zu zeigen, dass eine überabzählbare Teilmenge enthält. Wir betrachten dazu die Menge
,
also die Menge aller Dezimalzahlen zwischen 0 und 1, deren Nachkommastellen nur mit 0 oder 1 besetzt sind.
Die Elemente von R stehen in einem direkten Verhältnis zu den Teilmengen von , denn bezeichnet man für eine solche Teilmenge mit diejenige Zahl bei der ist, genau dann wenn (also z.B. oder oder auch ), so ist die Funktion gegeben durch
bijektiv. Jede Zahl besitzt nämlich genau ein Urbild, und zwar die Menge derjenigen mit .
R ist damit nicht abzählbar, denn anderenfalls wäre auch die zu R gleichmächtige Menge abzählbar. Dies aber ist nach [4.8.13] nicht wahr.
|
|
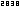 |
|
 haben wir die Möglichkeit, ihn als Gitterpunkt der Zeichenebene zu sehen.
haben wir die Möglichkeit, ihn als Gitterpunkt der Zeichenebene zu sehen.