4.6. Die Komposition von Funktionen

Neben den vier Grundrechenarten gibt es noch eine fünfte Methode, zwei Funktionen zu einer weiteren zu verbinden. Sie ist ganz auf den Charakter der Funktionen abgestellt, nämlich dem Zuweisen von Elementen einer Menge zu denen einer anderen, und daher nicht auf irgendwelche speziellen Gegebenheiten, wie etwa die Reellwertigkeit, angewiesen. So lässt sich etwa das bloße Zuweisen beliebig nacheinander durchführen. Die folgende Skizze macht diesen Gedanken deutlich.

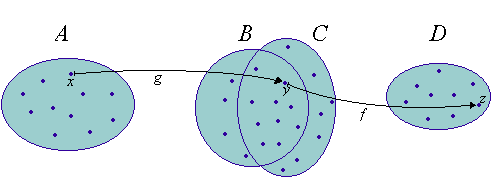
So wird hier dem Element

x \in A

mittels g das Element

y \in B

zugeordnet, das nun seinerseits durch die Funktion f auf das Element

z \in D

abgebildet wird. Blendet man den Zwischenschritt aus, so entsteht eine neue Zuordnung, die x direkt auf z abbildet.

Die Skizze zeigt auch bereits die typischerweise auftretenden Konstellationen:

Es gibt Elemente $x \in A$ , deren g-Bild zwar existiert, das aber von f nicht weiter transportiert werden kann. Dies schränkt sofort den Definitionsbereich der neuen Funktion ein!
Der Definitionsbereich von f enthält Elemente, die gar keine g-Bilder sind.

Definition: Sind $g : A \to B$ und $f : C \to D$ zwei Funktionen, so heißt die Funktion

f \circ g : {x \in A | g (x) \in C} \to D

gegeben durch

f \circ g (x) ≔ f (g (x))

[4.6.1]

die Hintereinanderausführung (oder auch die Komposition) von f nach g.

Beachte:

Der Bildbereich von $f \circ g$ ist per Definition die Menge D, also der Bildbereich der linken Funktion f.
Der Definitionsbereich von $f \circ g$ ist immer eine Teilmenge von A, also eine Teilmenge des Definitionsbereichs der rechten Funktion g.
Falls allerdings der Wertebereich von g vollständig im Definitionsbereich von f liegt, ist $f \circ g$ eine Funktion von (ganz) A nach D.
Haben C und der Wertebereich von g keine gemeinsamen Elemente, so ist $f \circ g$ die leere Funktion von $\emptyset$ nach D.
Beim Ausrechnen der neuen Funktionswerte benötigt man nur diejenigen Elemente von C, die ein g-Urbild besitzen.

Beispiel: Bei den folgenden Hintereinanderausführungen ermitteln wir jeweils den Definitions- und den Bildbereich, sowie die Funktionsvorschrift.

Der Bildbereich ist immer der Bildbereich der linken Funktion, so dass man hier wenig Mühe hat; auch die Funktionsvorschrift ist meist schnell notiert. Die eigentliche Arbeit steckt in Ermittlung des neuen Definitionsbereichs.

Oft lässt sich eine Hintereinanderausführung auch kompositionsfrei schreiben.

$X^{2} \circ (2 X + 4) : {x \in ℝ | 2 x + 4 \in ℝ} = ℝ \to ℝ$
$ℝ$ ist tatsächlich wieder der neue Definitionsbereich, denn die Bedingung $2 x + 4 \in ℝ$ wird von jedem x erfüllt. Also kann jede Zahl in die neue Funktion eingesetzt werden. Der Funktionswert im Punkt 3 etwa berechnet sich zu:

$X^{2} \circ (2 X + 4) (3) = X^{2} (2 X + 4 (3)) = X^{2} (10) = 100$ .

Allgemein gilt für jedes $x \in ℝ$ :
$X^{2} \circ (2 X + 4) (x) = X^{2} (2 X + 4 (x)) = X^{2} (2 x + 4) = {(2 x + 4)}^{2}$ ,

womit offenbar die Gleichheit $X^{2} \circ (2 X + 4) = {(2 X + 4)}^{2}$ erwiesen ist.
$(2 X + 4) \circ X^{2} : {x \in ℝ | x^{2} \in ℝ} = ℝ \to ℝ$
Die Bedingung $x^{2} \in ℝ$ wird auch hier wieder von jedem x erfüllt. Für $x = 3$ erhält man jetzt allerdings:

$(2 X + 4) \circ X^{2} (3) = 2 X + 4 (X^{2} (3)) = 2 X + 4 (9) = 22$ .

In ähnlicher Weise ergibt sich die Funktionsvorschrift zu:
$(2 X + 4) \circ X^{2} (x) = 2 X + 4 (X^{2} (x)) = 2 X + 4 (x^{2}) = 2 x^{2} + 4$ ,

Also hat man hier: $(2 X + 4) \circ X^{2} = 2 X^{2} + 4$ .
$\sqrt{X} \circ (2 X + 4) : {x \in ℝ | 2 x + 4 \in ℝ^{\geq 0}} = {x \in ℝ | 2 x + 4 \geq 0} = ℝ^{\geq - 2} \to ℝ$
In diesem Beispiel erfüllt nicht mehr jedes x die geforderte Bedingung; vielmehr ist jetzt der Definitionsbereich die Lösungsmenge einer Ungleichung:
$2 x + 4 \geq 0 \Leftrightarrow x \geq - 2$ .

Als Rechenbeispiel ermitteln wir den Funktionswert in 6:
$\sqrt{X} \circ (2 X + 4) (6) = \sqrt{X} (2 X + 4 (6)) = \sqrt{X} (16) = 4$ .

Oder allgemein für ein $x \geq - 2$ :
$\sqrt{X} \circ (2 X + 4) (x) = \sqrt{X} (2 X + 4 (x)) = \sqrt{X} (2 x + 4) = \sqrt{2 x + 4}$ .
$X^{2} \circ X^{2} : {x \in ℝ | x^{2} \in ℝ} = ℝ \to ℝ$
Weil $X^{2} \circ X^{2} (x) = X^{2} (X^{2} (x)) = X^{2} (x^{2}) = x^{4}$ , hat man hier offenbar:
$X^{2} \circ X^{2} = X^{4}$ .
$\frac{1}{X} \circ (2 X + 4) : {x \in ℝ | 2 x + 4 \in ℝ^{\neq 0}} = {x \in ℝ | 2 x + 4 \neq 0} = ℝ^{\neq - 2} \to ℝ$
Aus $2 x + 4 = 0 \Leftrightarrow x = - 2$ lässt sich der angegebene Definitionsbereich leicht ermitteln. Man darf also etwa rechnen:

$\frac{1}{X} \circ (2 X + 4) (- 1) = \frac{1}{X} (2 X + 4 (- 1)) = \frac{1}{X} (2) = \frac{1}{2}$ .

Aus der Funktionsvorschrift
$\frac{1}{X} \circ (2 X + 4) (x) = \frac{1}{X} (2 X + 4 (x)) = \frac{1}{X} (2 x + 4) = \frac{1}{2 x + 4}, x \neq - 2$

erhält man die Funktionengleichung:
$\frac{1}{X} \circ (2 X + 4) = \frac{1}{2 X + 4}$ .
$\frac{1}{X} \circ (X^{2} + 2 X + 4) : {x \in ℝ | x^{2} + 2 x + 4 \in ℝ^{\neq 0}} = ℝ \to ℝ$
Da die quadratische Gleichung $x^{2} + 2 x + 4 = 0$ keine Lösung besitzt, ist kein x von der genannten Bedingung betroffen. Also ist der neue Definitionsbereich wieder $ℝ$ . Ähnlich wie im letzen Beispiel lässt sich die neue Funktion auch kompositionsfrei schreiben:
$\frac{1}{X} \circ (X^{2} + 2 X + 4) = \frac{1}{X^{2} + 2 X + 4}$ .

Für die weiteren Ausführungen ist es günstig, das Konzept der konstanten Funktionen und der Identität etwas zu verallgemeinern.

Für eine beliebige Menge A bzw. für ein beliebiges Element $c \in B$ nennen wir die Funktion

$c_{A} : A \to B$ gegeben durch $c_{A} (x) ≔ c$ die konstante Funktion c auf A.	[4.6.2]
$X_{A} : A \to A$ gegeben durch $X_{A} (x) ≔ x$ die Identität auf A.	[4.6.3]

Die bereits in Abschnitt 2 angesprochene Notation $c = c_{ℝ}$ , bzw. $X = X_{ℝ}$ ordnet sich hier offenbar unter.

Das Verhalten der Identitäten und der konstanten Funktionen bei der Komposition ist schnell geklärt.

Bemerkung: $f : A \to B$ sei eine beliebige Funktion und $c \in A$ ; dann gilt:

$f \circ X_{A} = f = X_{B} \circ f$ .	[4.6.4]
$c_{B} \circ f = c_{A}$ .	[4.6.5]
$f \circ c_{A} = f {(c)}_{A}$ .	[4.6.6]

Falls $A = B = ℝ$ , darf man auf die Indices verzichten.

Beweis:

1. ► $f \circ X_{A} : {x \in A | x = X_{A} (x) \in A} = A \to B$ und $f \circ X_{A} (x) = f (X_{A} (x)) = f (x)$ .
Analog: $X_{B} \circ f : {x \in A | f (x) \in B} = A \to B$ und $X_{B} \circ f (x) = X_{B} (f (x)) = f (x)$ .

2. ► $c_{B} \circ f : {x \in A | f (x) \in B} = A \to A$ und $c_{B} \circ f (x) = c_{B} (f (x)) = c = c_{A} (x)$ .
Man beachte, dass hier die Situation $c_{B} : B \to A$ und $c_{A} : A \to A$ vorliegt.

3. ► $f \circ c_{A} : {x \in A | c = c_{A} (x) \in A} = A \to B$ und $f \circ c_{A} (x) = f (c_{A} (x)) = f (c) = f {(c)}_{A} (x)$ .
Außerdem hat man: $f {(c)}_{A} : A \to B$ .

Wir wenden uns nun den Rechenregeln für die Komposition zu.

Bemerkung:

$\circ$ ist nicht kommutativ.	[4.6.7]
$\circ$ ist assoziativ.	[4.6.8]

Beweis:

1. ► Hier reicht es, ein Gegenbeispiel zu nennen. Mit unseren anfänglichen Beispielen haben wir aber schon:

X^{2} \circ (2 X + 4) \neq (2 X + 4) \circ X^{2}

2. ► Wir geben uns drei Funktionen $h : A \to B, g : C \to D$ und $f : E \to F$ vor und überprüfen zunächst die Gleichheit der Bereiche:

\begin{array}{l} (f \circ g) \circ h : {x \in A | h (x) \in {x \in C | g (x) \in E}} = {x \in A | h (x) \in C \land g (h (x)) \in E} \to F \\ f \circ (g \circ h) : {x \in {x \in A | h (x) \in C} | g (h (x)) \in E} = {x \in A | h (x) \in C \land g (h (x)) \in E} \to F \end{array}

und nun für ein x aus dem gemeinsamen Definitionsbereich die Gleichheit der Funktionswerte:

\begin{array}{l} (f \circ g) \circ h (x) = (f \circ g) (h (x)) = f (g (h (x)) \\ f \circ (g \circ h) (x) = f (g \circ h (x)) = f (g (h (x)) \end{array}

Bei reellwertigen Funktionen tritt die Hintereinanderausführung in Kontakt zu den vier Grundrechenarten. Interessant ist hier die Untersuchung auf distributives Verhalten. Da $\circ$ nicht kommutativ ist, muß man zwischen links- und rechtsdistributiv unterscheiden, und in der Tat stellen sich auch unterschiedliche Ergebnisse ein. Wir vereinbaren gleichzeitig, zur Einsparung von Klammern, dass $\circ$ stärker binden soll als $+, -, \cdot$ und :.

Bemerkung:

$\circ$ verhält sich rechtsdistributiv zu den vier Grundrechenarten,	[4.6.9]
aber nicht linksdistributiv.	[4.6.10]

Beweis:

1. ► Wir zeigen beispielhaft das Distributivgesetz für die Multiplikation. Dazu geben wir uns drei reellwertige Funktionen $h : A \to ℝ, g : B \to ℝ$ und $f : C \to ℝ$ vor und untersuchen auch hier zunächst die Bereiche:

\begin{array}{l} (f \cdot g) \circ h : {x \in A | h (x) \in C \cap B} \to ℝ \\ f \circ h \cdot g \circ h : {x \in A | h (x) \in C} \cap {x \in A | h (x) \in B} = {x \in A | h (x) \in C \cap B} \to ℝ \end{array}

und anschließend die Funktionsvorschriften:

(f \cdot g) \circ h (x) = (f \cdot g) (h (x)) = f (h (x)) \cdot g (h (x)) = f \circ h (x) \cdot g \circ h (x) = f \circ h \cdot g \circ h (x)

2. ► Mit [4.6.5] haben wir etwa für die Addition:

7 \circ (X + 1) = 7

, aber

7 \circ X + 7 \circ 1 = 7 + 7 = 14

Wenn auch die Komposition gegenüber den Grundrechenarten nicht linksdistributiv ist, so spielen die Potenzfunktionen als linker Partner eine interessante Rolle:

Bemerkung: Ist $f : A \to ℝ$ eine reellwertige Funktion, so gilt:

X^{n} \circ f = f^{n}

[4.6.11]

Insbesondere also: $\frac{1}{X} \circ f = \frac{1}{f}$ .

Beweis: Beim Überprüfen der Bereiche
i

Zur Erinnerung:

$f^{n} : A \to ℝ$ , falls $n \geq 0$

$f^{n} : {x \in A | f (x) \neq 0} \to ℝ$ , falls $n < 0$ .

unterscheiden wir zwei Fälle:

\begin{array}{l} n \geq 0 : X^{n} \circ f : {x \in A | f (x) \in ℝ} = A \to ℝ \\ n < 0 : X^{n} \circ f : {x \in A | f (x) \in ℝ^{\neq 0}} = {x \in A | f (x) \neq 0} \to ℝ \end{array}

Für die Funktionsvorschriften hat in jedem Fall

X^{n} \circ f (x) = X^{n} (f (x)) = {(f (x))}^{n} = f^{n} (x)

Als rechter Partner haben dagegen nur die Linearfaktoren $X - a$ eine besondere Bedeutung:

Bemerkung: Ist $A \subset ℝ$ und $f : A \to ℝ$ eine reellwertige Funktion, so entsteht der Graph von $f \circ (X - a)$ durch Verschieben des Graphen von f um a Einheiten in der Waagerechten.

Kombiniert man dies mit dem Addieren konstanter Funktionen, erhält man die allgemeine Verschiebungsregel: Verschiebt man f um a Einheiten in der Waagerechten und um b Einheiten in der Senkrechten, so entsteht die Funktion

f \circ (X - a) + b

[4.6.12]

Beweis: Wir berechnen zunächst den Definitionsbereich von $f \circ (X - a)$ :

{x \in ℝ | x - a = (X - a) (x) \in A} = {x + a | x \in A}

Also erhält man den neuen Definitionsbereich, indem zu jedem Element von A die Zahl a zugezählt wird; dies ist eine Verschiebung um a Einheiten nach rechts, falls a positiv, nach links, falls a negativ ist.

Die neue Funktion nimmt nun auf dem neuen Definitionsbereich die alten Werte an:

f \circ (X - a) (x + a) = f (x + a - a) = f (x)

Addiert man schließlich noch die konstante Funktion b, so ändert sich der Definitionsbereich nicht mehr: ${x + a | x \in A} \cap ℝ = {x + a | x \in A}$ , da $A \subset ℝ$ . Es werden nur noch die Funktionswerte um b Einheiten angehoben, bzw. abgesenkt.

Es lohnt sich, die folgenden Beispiele zu [4.6.12] über einen Funktionenplotter zu visualisieren. Die angegebenen Verschiebungen können dann direkt gesehen werden.

Beispiel:

${(X - 3)}^{2} - 5 = X^{2} \circ (X - 3) - 5$ ist die um 3 in der Waagerechten und −5 in der Senkrechten verschobene Quadratfunktion.
$H (X + 8) - 4 = H \circ (X + 8) - 4$ ist die um −8 in der Waagerechten und −4 in der Senkrechten verschobene Heavisidefunktion.
$\frac{1}{X + 2} + 7 = \frac{1}{X} \circ (X + 2) + 7$ ist die um −2 in der Waagerechten und 7 in der Senkrechten verschobene Kehrwertfunktion.
$\sin (X - 3 π) = \sin \circ (X - 3 π)$ ist die um 3π in der Waagerechten verschobene Sinusfunktion.

Zum Ende dieses Teils vereinbaren wir noch eine schreibtechnische Erleichterung (die auch schon stillschweigend benutzt wurde). Gelegentlich, wenn es zu keinen Mißverständnissen führt, schreiben wir $f (g)$ statt $f \circ g$ , also z.B. $\sin (\cos)$ statt $\sin \circ \cos$ .

4.5. 4.7.