Every Continuous Function on an Interval has a Primitive

We distinguish between several types of intervals:
 

1. Every continuous function ${\displaystyle f:[\mathrm{0,1}]\to ℝ}$ has a primitive.

   Proof:  We use the Weierstrass approximation theorem (click for an alternative ad hoc proof). According to [6.7.2] there is a sequence of polynomials ${\displaystyle (p_n)}$ that converges uniformely on ${\displaystyle [0,1]}$ to f:

   ${\displaystyle p_n\underset{gm}{\to }f}$

   As every polynomial ${\displaystyle p_n}$ is integrable due to [8.1.10], the uniform limit f has a primitive according to [8.1.15].

   Proof:  For each ${\displaystyle n\in {\mathbb{N}}^{*}}$ we will construct a traverse  ${\displaystyle p_n}$ (a much shorter proof directly uses the Bernstein polynomials) that connects ${\displaystyle n+1}$ suitable points of f. To that end we section the interval ${\displaystyle [\mathrm{0,1}]}$ into n subintervals of length ${\displaystyle \frac{1}{n}}$ and define for ${\displaystyle 0\le i\le n-1}$

   ${\displaystyle I_{n,i}}$
   

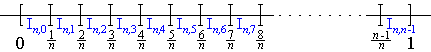
   These subintervals correspond to ${\displaystyle n+1}$ points of f. We now connect the ith one to the (${\displaystyle i+1}$)th one by the line segment

   ${\displaystyle g_{n,i}:I_{n,i}\to ℝ,x\mapsto m_{n,i}\cdot (x-\frac{i}{n})+f(\frac{i}{n})}$

   where the slope ${\displaystyle m_{n,i}}$ is calculated by the quotient

   ${\displaystyle m_{n,i}=\frac{f(\frac{i+1}{n})-f(\frac{i}{n})}{\frac{1}{n}}=n(f(\frac{i+1}{n})-f(\frac{i}{n}))}$.

   For ${\displaystyle 0\le i<n-1}$ we have ${\displaystyle I_{n,i}\cap I_{n,i+1}=\{\frac{i+1}{n}\}}$ and

   ${\displaystyle g_{n,i}(\frac{i+1}{n})=m_{n,i}\cdot \frac{1}{n}+f(\frac{i}{n})=f(\frac{i+1}{n})-f(\frac{i}{n})+f(\frac{i}{n})=g_{n,i+1}(\frac{i+1}{n})}$,

   so that we can take the well defined concatenation

   i

   For ${\displaystyle f:A\to ℝ}$ and ${\displaystyle g:B\to ℝ}$ with  ${\displaystyle f(x)=g(x)}$ for all ${\displaystyle x\in A\cap B}$ we set ${\displaystyle f\cup g(x)=\{\begin{array}{l}f(x)\text{, if }x\in A\hfill \\ g(x)\text{, if }x\in B\hfill \end{array}}$

   ${\displaystyle p_n≔g_{n\mathrm{,0}}\cup \dots \cup g_{n,n-1}}$

   as the traverse we were looking for. A callable applet

   i

   exemplifies by the function ${\displaystyle f:[0,1]\to ℝ}$, ${\displaystyle x\mapsto 5x\cdot \cos (20x)}$ how the sequence of traverses approximates the function f.

   Every line segment ${\displaystyle g_{n,i}}$ is the restriction of a linear function and hence integrable (see [8.1.10], [8.1.13]). Along with the line segments the traverses ${\displaystyle p_n}$ are integrable as well due to [8.1.14]. The desired integrability of f thus will follow from [8.1.15] if we could prove the uniform convergence

   ${\displaystyle p_n\underset{uf}{\to }f}$.

   To that end let ${\displaystyle x\in [\mathrm{0,1}]}$ and ${\displaystyle \epsilon >0}$ be arbitrary. As f is uniformely continuous on the closed interval ${\displaystyle [0,1]}$ there is an ${\displaystyle n_0\in {\mathbb{N}}^{\ast }}$ such that all ${\displaystyle r,s\in [0,1]}$ satisfy the condition

   ${\displaystyle |r-s|\le \frac{1}{n_0}\Rightarrow |f(r)-f(s)|<\frac{\epsilon }{2}}$.

   For any ${\displaystyle n\ge n_0}$ we use this implication twice:

   • As ${\displaystyle |\frac{i+1}{n}-\frac{i}{n}|=\frac{1}{n}\le \frac{1}{n_0}}$ the slopes of the line segments could be estimated as follows:

     ${\displaystyle |m_{n,i}|=n|f(\frac{i+1}{n})-f(\frac{i}{n})|<n\frac{\epsilon }{2}}$  for all  ${\displaystyle 0\le i<n-1}$.
     
      

   • x is a member of one of the intervals ${\displaystyle I_{n,i}}$, say ${\displaystyle x\in I_{n,i_n}}$. Thus we have ${\displaystyle p_n(x)=g_{n,i_n}(x)}$ and ${\displaystyle |\frac{i_n}{n}-x|\le \frac{1}{n}\le \frac{1}{n_0}}$, so we know:

     ${\displaystyle \begin{array}{ll}|p_n(x)-f(x)|\hfill & =|g_{n,i_n}(x)-f(x)|\hfill \\ \hfill & =|m_{n,i_n}\cdot (x-\frac{i_n}{n})+f(\frac{i_n}{n})-f(x)|\hfill \\ \hfill & \le |m_{n,i_n}|\cdot |x-\frac{i_n}{n}|+|f(\frac{i_n}{n})-f(x)|\hfill \\ \hfill & <n\cdot \frac{\epsilon }{2}\cdot \frac{1}{n}+\frac{\epsilon }{2}=\epsilon \text{.}\hfill \end{array}}$
   
    

2. Every continuous function ${\displaystyle f:[a,b]\to ℝ}$ has a primitive.

   Proof:  The function ${\displaystyle f\circ (a+(b-a)\cdot \mathrm{X})}$ is continuous on ${\displaystyle [0,1]}$ and thus has a primitive g according to 1. With the chain rule [7.7.8] we see that

   ${\displaystyle h≔(b-a)(g\circ \frac{\mathrm{X}-a}{b-a})}$

   is differentiable with ${\displaystyle h^{\prime }=(b-a)(g^{\prime }\circ \frac{\mathrm{X}-a}{b-a})\frac{1}{b-a}=f\circ (a+(b-a)\cdot \mathrm{X})\circ \frac{\mathrm{X}-a}{b-a}=f}$.
   h is thus a primitive function of f.

   
    

3. Every continuous function ${\displaystyle f:I\to ℝ}$ has a primitive.

   Proof:  Closed intervals are covered by 2, so we only need to consider intervals I of the type ${\displaystyle ]a,b[}$, ${\displaystyle ]a,b]}$ or ${\displaystyle [a,b[}$. As an example we will assume I is of the latter type. I may be represented as the union of an increasing sequence ${\displaystyle (I_n)}$ of closed subintervals: ${\displaystyle I=\underset{i\in \mathbb{N}}{\cup }{I}_n}$. Take for instance

   ${\displaystyle I_n≔\{\begin{array}{l}[a,b-\frac{b-a}{n+1}]\text{ , if }b<\infty \hfill \\ [a,a+n]\text{ , if }b=\infty \hfill \end{array}}$

   f is continuous, and thus integrable, on each of these closed intervals. Due to [8.1.3] there is a unique differentiable function ${\displaystyle g_n:I_n\to ℝ}$ for each ${\displaystyle n>1}$ such that ${\displaystyle g_n(a)=0}$ and ${\displaystyle {g_n}^{\prime }(x)=f(x)}$ for all ${\displaystyle x\in I_n}$.

   The uniqueness guarantees for any ${\displaystyle m\ge n>1}$ that

   ${\displaystyle g_m(x)=g_n(x)}$ for all ${\displaystyle x\in I_n}$.

   Setting

   ${\displaystyle g(x)≔g_n(x)}$, if ${\displaystyle x\in I_n}$ for an appropriate n

   thus yields a well defined function ${\displaystyle g:I\to ℝ}$ that coincides locally at each x with one of the functions ${\displaystyle g_n}$. Hence g is differentiable with ${\displaystyle g^{\prime }=f}$.