7.7. The Derivative

When we started to study calculus our first objective was to create a tangent to a given function at a given, and naturally fixed point a. However most of our example functions turned out to be differentiable at many, in most cases even at all points of their domain.

This part now will bring the latter aspect into a sharper focus, i.e. we will change our point of view from a local to a global one.

Consider:

• If a function  ${\displaystyle f:B\to ℝ}$ is differentiable at ${\displaystyle x\in A}$ the point x has to be an accumulation point

  i

  i.e. there is a sequence ${\displaystyle (a_n)}$ in B such that ${\displaystyle x\ne a_n\to x}$.

  of B. In the following we thus confine ourselves to those sets A which only have elements that are accumulation points of A (and thus of B as well).
   

• As before, we take account of the special notation in physics (cf. [7.3]) and usually replace ${\displaystyle s^{\prime }}$ by ${\displaystyle \dot{s}}$ for differentiable functions of the type ${\displaystyle t\mapsto s(t)}$.

  
   

We now restate some of the old examples from 7.3, 7.4, 7.5 and 7.6 in our new language:

• ${\displaystyle c,\mathrm{X},m\mathrm{X}+b,{\mathrm{X}}^n,\exp ,\sin ,\cos \in {\mathcal{D}}^1(ℝ)}$ and

  ${\displaystyle c^{\prime }=0}$

  ${\displaystyle {\mathrm{X}}^{\prime }=1}$

  ${\displaystyle (m\mathrm{X}+b{)}^{\prime }=m}$

  ${\displaystyle ({\mathrm{X}}^n{)}^{\prime }=n{\mathrm{X}}^{n-1}}$

  ${\displaystyle {\exp }^{\prime }=\exp }$

  ${\displaystyle {\sin }^{\prime }=\cos }$

  ${\displaystyle {\cos }^{\prime }=-\sin }$

• ${\displaystyle \frac{1}{\mathrm{X}}\in {\mathcal{D}}^1({ℝ}^{\ne 0})}$ and  ${\displaystyle (\frac{1}{\mathrm{X}}{)}^{\prime }=-\frac{1}{{\mathrm{X}}^2}}$

• ${\displaystyle \sqrt{\mathrm{X}}\in {\mathcal{D}}^1({ℝ}^{>0})}$ and  ${\displaystyle {\sqrt{\mathrm{X}}}^{\prime }=\frac{1}{2\sqrt{\mathrm{X}}}}$.  but consider:  ${\displaystyle \sqrt{\mathrm{X}}\notin {\mathcal{D}}^1({ℝ}^{\ge 0})}$

• ${\displaystyle |\mathrm{X}|\in {\mathcal{D}}^1({ℝ}^{\ne 0})}$ and  ${\displaystyle |\mathrm{X}{|}^{\prime }=\frac{|\mathrm{X}|}{\mathrm{X}}}$.  but consider:  ${\displaystyle |\mathrm{X}|\notin {\mathcal{D}}^1(ℝ)}$

• ${\displaystyle \tan \in {\mathcal{D}}^1(\{x\in ℝ|x\ne (2k-1)\frac{\pi }{2}\})}$ and  ${\displaystyle {\tan }^{\prime }=\frac{1}{{\cos }^2}}$

• ${\displaystyle \cot \in {\mathcal{D}}^1(\{x\in ℝ|x\ne k\pi \})}$ and  ${\displaystyle {\cot }^{\prime }=-\frac{1}{{\sin }^2}}$

• The limit function  ${\displaystyle f=\sum _{i=0}^{\infty }{a}_i{(\mathrm{X}-a)}^i}$ of a convergent power series is differentiable and

  ${\displaystyle f^{\prime }=\sum _{i=1}^{\infty }{a}_{i}i{(\mathrm{X}-a)}^{i-1}}$

It is not only the old examples that could be transformed into the new notation but a lot properties as well. For example the relation worked out in [7.5.2] could be noted in quite a compact shape:

The absolute value function proves that this inclusion could not be tightened to identity.

Differentiable functions have to be continuous. Interestingly this is no compulsory feature for the derivation function. (see an example in chapter 8). Thus the following definition truly extends our concept of differentiability.

In [7.6.1-4] and [7.6.11] resp. we stated the derivation rules in their local form. Of course they could be adapted to the new concept as well and it is in this form that they are more pleasant to the eye.

The various special cases mentioned in the last chapter have of course global versions as well. Assuming the premises in the proposition above we thus could calculate:

Similar to ${\displaystyle {\mathcal{C}}^0(A)}$ in [6.3] the sets ${\displaystyle {\mathcal{D}}^1(A)}$ and ${\displaystyle {\mathcal{C}}^1(A)}$ could be fitted out with an algebraic structure. As ${\displaystyle 0|A\mathrm{,1}|A\in {\mathcal{C}}^1(A)}$ we conclude from [7.7.4-6]:

• ${\displaystyle ({\mathcal{D}}^1(A),+)}$ and ${\displaystyle ({\mathcal{C}}^1(A),+)}$ are abelian groups

  i

  The addition + is associative and commutative. 0 is the neutral element, i.e.  ${\displaystyle f+\mathbf{0}=f}$  for all  f. Each f has a unique inverse, ${\displaystyle -f}$ in this case, such that  ${\displaystyle f+(-f)=\mathbf{0}}$.

  .
• ${\displaystyle ({\mathcal{D}}^1(A),+,\cdot )}$ and ${\displaystyle ({\mathcal{C}}^1(A),+,\cdot )}$ are commutative rings with identity element

  i

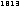  The axioms for an abelian group are satisfied. The multiplication · is associative and commutative. · is distributive with respect to +. 1 is the neutral element for the multiplication, i.e. ${\displaystyle \mathbf{1}·f=f}$ for all f.

  .

7.6.

7.8.