7.8. Repeatedly Differentiable Functions

At a first glance the only advantage when switching from the local to the global view seems to have a concise and compact notation at hand. At a closer inspection however we see that for a derivation function - in contrast to a deriviation number - there is an option for a further check for differentiability. Thus we might be able to create in turn the functions

f^{'}, {f^{'}}^{'}, {f^{'}}^{'}^{'}, \dots

, a feature that actually adds a new quality to our theory.

To capture the idea of a repeatedly differentiable function in true mathematical terms turns out to be a bit cumbersome, as inevitably recursive techniques are to be used.

Definition: Take $\emptyset \neq A \subset B$ and an arbitrary $n \in ℕ^{*}$ . We call a function $f : B \to ℝ$

1-time differentiable on A if f is differentiable on A and say that the function $f^{(1)} ≔ f^{'}$ is the first derivative of f.
(n + 1)-times differentiable on A if f is n-times differentiable on A and the nth derivative $f^{(n)}$ is differentiable on A as well. The function $f^{(n + 1)} ≔ (f^{(n)})^{'}$ is said to be the (n + 1)th derivative of f.

[7.8.1]

$f^{(n)}$ is read as "f n" and $f^{(0)} ≔ f$ is regarded as the derivate of order zero. In most cases we use the prime-notation for the first few n: ${f^{'}}^{'} ≔ f^{(2)}$ , ${f^{'}}^{'}^{'} ≔ f^{(3)}$ etc.

$D^{n} (A)$ denotes the set of all n-times differentiable functions, the so called $D^{n}$ -functions, on A.

A function $f \in D^{n} (A)$ is called n-times continuously differentiable on A, or a $C^{n}$ -function, if the nth derivative $f^{(n)}$ is continuous. The set of all $C^{n}$ -functions is denoted by $C^{n} (A)$ .

$C^{\infty}$ -functions, i.e. the functions in

C^{\infty} (A) ≔ \underset{n \in ℕ^{*}}{\cap} C^{n} (A) = \underset{n \in ℕ^{*}}{\cap} D^{n} (A)

belong to each $D^{n} (A)$ , so they are arbitrary often differentiable.

Consider:

Again, in physics, we introduce the dot notation (cf. [7.3]) $\dot{s}, \ddot{s}, \overset{⃛}{s}, \dots$ for the derivatives of repeatedly differentiable functions of the $t \mapsto s (t)$ type. The second derivative is usually replaced by the symbol $a (t) = \ddot{s} (t)$
i

a for acceleration from the Latin acceleratio.

and is regarded as the acceleration at the time t.

Due to the recursive nature of the above definition it is often quite tedious to prove a function to be repeatedly differentiable. For example, to see that a function is 4-times differentiable we need to know first that it is 3-times differentiable, which in turn requires the double differentiability and so on. We demonstrate this procedure with the cube function $X^{3}$ .

As $X^{n}$ is differentiable ([7.3.3]) we could use the factor rule [7.7.10] to form the following line of results:

$X^{3}$	is 1-time differentiable and $(X^{3})^{'} = 3 X^{2} \in D^{1} (ℝ)$
$\Rightarrow X^{3}$	is 2-times differentiable and $(X^{3} {)^{'}}^{'} = (3 X^{2})^{'} = 6 X \in D^{1} (ℝ)$
$\Rightarrow X^{3}$	is 3-times differentiable and $(X^{3} {)^{'}}^{'}^{'} = (6 X)^{'} = 6 \in D^{1} (ℝ)$
$\Rightarrow X^{3}$	is 4-times differentiable and $(X^{3})^{(4)} = 6^{'} = 0 \in D^{1} (ℝ)$

Furthermore the last result shows that $X^{3}$ is even a $C^{\infty}$ -function with all its derivatives of order 4 and higher being equal to 0.

Proving that a certain function f is, let's say, 10-times differentiable is - according to [7.8.1] - actually the task to show that $f^{(9)}$ is differentiable a further time. But maybe with that function it is easier to prove the 9-times differentiability of $f^{'}$ or to show that $f^{(7)}$ is still 3-times differentiable. It is interesting to see that we are allowed to follow these temptations getting the same result whatever variant we decided to go for.

Proposition: Take $n, k \in ℕ^{*}$ . For $1 \leq k < n$ we have:

f \in D^{n} (A) \Leftrightarrow f \in D^{k} (A) \land f^{(k)} \in D^{n - k} (A)

[7.8.2]

If f is n-times differentiable on A then $f^{(n)} = (f^{(k)})^{(n - k)}$ .

Proof by induction on n:

There is nothing to prove for $n = 1$ as there are no incidences for $k < n$ .
Now let the equivalence [7.8.2] be valid and the associated derivation formula as well. We have to show for $1 \leq k < n + 1$ :

$f \in D^{n + 1} (A) \Leftrightarrow f \in D^{k} (A) \land f^{(k)} \in D^{n + 1 - k} (A)$

as well as $f^{(n + 1)} = (f^{(k)})^{(n + 1 - k)}$ . If $k = n$ all this is already true by definition [7.8.1] so that we may assume $k < n$ for the remainder.

" $\Rightarrow$ " Take $f \in D^{n + 1} (A)$ , i.e. $f \in D^{n} (A)$ , $f^{(n)} \in D^{1} (A)$ and $f^{(n + 1)} = (f^{(n)})^{'}$ .
Due to the induction hypothesis we have $f \in D^{k} (A)$ and $f^{(k)} \in D^{n - k} (A)$ with

$(f^{(k)})^{(n - k)} = f^{(n)} \in D^{1} (A)$ .

Thus we know: $f^{(k)} \in D^{n - k + 1} (A)$ and $(f^{(k)})^{(n - k + 1)} = (f^{(n)})^{'} = f^{(n + 1)}$ .

" $\Leftarrow$ " Now take $f \in D^{k} (A)$ such that $f^{(k)} \in D^{n + 1 - k} (A)$ .
According to [7.8.1] this means: $f^{(k)} \in D^{n - k} (A)$ and $(f^{(k)})^{(n - k)} \in D^{1} (A)$ . From the induction hypothesis we see that $f \in D^{n} (A)$ and $f^{(n)} = (f^{(k)})^{(n - k)}$ , which in fact means: $f^{(n)} \in D^{1} (A)$ . So $f \in D^{n + 1} (A)$ is true.

[7.8.2] is often used in the special case $k = 1$ :

$f \in D^{n} (A) \Leftrightarrow f \in D^{1} (A) \land f^{'} \in D^{n - 1} (A)$

[7.8.3]

which allows an alternative way to calculate the n-th derivative: $f^{(n)} = {(f^{'})}^{(n - 1)}$ .

Some obvious inclusions are valid between the various differentiability classes. Immediately with [7.8.2] we have for example with $1 \leq k < n$ :

$D^{n} (A) \subset D^{k} (A)$	[7.8.4]
$C^{n} (A) \subset C^{k} (A)$	[7.8.5]

And trivially:

$C^{\infty} (A) \subset C^{n} (A) \subset D^{n} (A)$

[7.8.6]

All these inclusions are true ones as the following proposition will show.

Proposition: For $n, k \in ℕ^{*}$ , $1 \leq k < n$ we have:

$D^{n} (A) \neq D^{k} (A)$	[7.8.7]
$C^{n} (A) \neq C^{k} (A)$	[7.8.8]
$C^{\infty} (A) \neq C^{n} (A) \neq D^{n} (A)$	[7.8.9]

Proof: Without restriction we only consider the case $A = ℝ$ . All subsequent counter examples work with 0 as critical point. With an appropriate shift along the x-axis such a critical point could be placed in an arbitrary set A, so that the general situation is covered as well.

Furthermore we note that the counter example in 2. also serves as a counter example for 1.

2. ► At first we consider for any $n \in ℕ^{*}$ the function

f_{n} ≔ X^{n} \cdot | X |

Due to the product rule ([7.6.3], see also [7.4.3] for the derivative of the absolute value function) $f_{n}$ is differentiable at each $x \neq 0$ and

{f_{n}}^{'} (x) = n \cdot x^{n - 1} \cdot | x | + x^{n} \cdot \frac{| x |}{x} = (n + 1) \cdot x^{n - 1} \cdot | x |

For the differentiability at 0 we have to calculate the limit of the difference quotient function:

\lim_{x \to 0} \frac{x^{n} \cdot | x |}{x} = \lim_{x \to 0} x^{n - 1} \cdot | x | = 0 = (n + 1) \cdot 0^{n - 1} \cdot | 0 |

Combining these two results we get: $f_{n} \in C^{1} (ℝ)$ and ${f_{n}}^{'} = (n + 1) \cdot X^{n - 1} \cdot | X |$ .

Now we are prepared for the actual proof. It is only necessary to handle the case $k = n - 1$ and to that end we will prove by induction on $n \geq 2$ : $f_{n - 1}$ is a member of $C^{n - 1} (ℝ)$ but not of $D^{n} (ℝ)$ and thus does not belong to $C^{n} (ℝ)$ either.

Take $n = 2$ . Due to our preliminary result $f_{1}$ is a $C^{1}$ -function, failing to be a $D^{2}$ -function as ${f_{1}}^{'} = 2 \cdot | X | \notin D^{1} (ℝ)$ .
According to the induction hypothesis ${f_{n}}^{'} = (n + 1) \cdot f_{n - 1}$ is $C^{n - 1}$ but not $D^{n}$ . Due to [7.8.3] we thus know: $f_{n}$ is a $C^{n}$ -function missing in $D^{n + 1} (ℝ)$ .

3. ► We prove the assertion $C^{n} (ℝ) \neq D^{n} (ℝ)$ by induction: For each n there is a function $f_{n} \in D^{n} (ℝ)$ such that its nth derivative is discontinuous.

Setting $f_{1} (x) = {\begin{array}{l} x^{2} \cdot \sin \frac{1}{x}, if x \neq 0 \\ 0, if x = 0 \end{array}$ yields a differentiable function $f_{1}$ with discontinuous derivative due to an example in part 8.
Take an $f_{n} \in D^{n} (ℝ)$ with discontinuous derivative ${f_{n}}^{(n)}$ . As $f_{n}$ itself is continuous (see [7.5.2]) the theorem [8.1.5] provides a differentiable function $f_{n + 1}$ such that ${f_{n + 1}}^{'} = f_{n}$ . Due to [7.8.3] this means: $f_{n + 1} \in D^{n + 1} (ℝ)$ and ${f_{n + 1}}^{(n + 1)} = {f_{n}}^{(n)}$ is discontinuous.

The assertion $C^{\infty} (ℝ) \neq C^{n} (ℝ)$ is a direct consequence of [7.8.8].

So far $C^{\infty} (A)$ is our smallest class of differentiable functions. Nevertheless it is a quite extensive one. In this context the limit functions of convergent power series play an interesting role: From 7.7. we know that their derivatives are limit functions again, which - by an inductive argument - leads to: Limit functions of convergent power series are arbitrary often differentiable.

As an analytical function coincides locally with the limit function of a convergent power series we may extend [7.8.9] by

C^{*} (A) \subset C^{\infty} (A)

[7.8.10]

a true inclusion as well due to the so called $C^{\infty}$ -hats, special non-zero $C^{\infty}$ -functions, created in 9.12 that evaluate to zero everywhere except for a closed interval. Due to the identity theorem [5.12.13] they thus fail to be analytical.

The analytical functions exp, sin and cos for example are easy to derivate:

$\exp^{(n)} = \exp$	$\sin^{(n)} = {\begin{array}{l} \cos & , if n = 4 k + 1 \\ - \sin & , if n = 4 k + 2 \\ - \cos & , if n = 4 k + 3 \\ \sin & , if n = 4 k \end{array}$	$\cos^{(n)} = {\begin{array}{l} - \sin & , if n = 4 k + 1 \\ - \cos & , if n = 4 k + 2 \\ \sin & , if n = 4 k + 3 \\ \cos & , if n = 4 k \end{array}$
[7.8.11]	[7.8.12]	[7.8.13]

Polynomials, analytical functions as well, are rather special in respect of repeated differentiability: Each derivative will lower the degree of polynomial p by one unit, consequently ending up with $p^{(g r a d p + 1)} = 0$ . It is sufficient to prove this behaviour for monomials:

Proposition: All $n, k \in ℕ^{*}$ satisfy

(X^{k})^{(n)} = {\begin{array}{l} \frac{k!}{(k - n)!} X^{k - n},  if n \leq k \\ 0,  if n > k \end{array}

[7.8.14]

Proof: The case $n = 1$ is immediately calculated:

(X^{k})^{'} = k X^{k - 1} = \frac{k!}{(k - 1)!} X^{k - 1}

If $n > 1$ we start an induction on k:

The case $k = 1$ is done by $X^{(n)} = {(X^{'})}^{(n - 1)} = 1^{(n - 1)} = 0$ .
Now let the equality [7.8.14] be valid for a fixed k. We thus may calculate as follows:

$\begin{array}{l} (X^{k + 1})^{(n)} & = ((X^{k + 1})^{'})^{(n - 1)} \\ = (k + 1) (X^{k})^{(n - 1)} \\ = {\begin{array}{l} (k + 1) \frac{k!}{(k - (n - 1))!} X^{k - (n - 1)}, if n - 1 \leq k \\ 0, if n - 1 > k \end{array} \\ = {\begin{array}{l} \frac{(k + 1)!}{(k + 1 - n)!} X^{k + 1 - n}, if n \leq k + 1 \\ 0, if n > k + 1 \end{array} \end{array}$

We will now focus on the algebraic properties of the various differentiability classes. The crucial question to this issue is if the derivation rules are transferable. The answer is simple for the sum and the difference rule.

Proposition: For all $n \in ℕ^{*}$ we have: $f, g \in D^{n} (a) \Rightarrow$

$f + g \in D^{n} (A)$ and ${(f + g)}^{(n)} = f^{(n)} + g^{(n)}$	[7.8.15]
$f - g \in D^{n} (A)$ and ${(f - g)}^{(n)} = f^{(n)} - g^{(n)}$	[7.8.16]
$c \cdot f \in D^{n} (A)$ and ${(c \cdot f)}^{(n)} = c \cdot f^{(n)}$	[7.8.17]

Proof: All proofs are by induction. The respective base steps ( $n = 1$ ) are already done in [7.7.4-6]. As an example we will do the induction step for the first assertion only.

If $f, g \in D^{n + 1} (A)$ we know that $f, g \in D^{n} (A)$ and $f^{(n)}, g^{(n)} \in D^{1} (A)$ . Due to the induction hypothesis this means $f + g \in D^{n} (A)$ and additionally

{(f + g)}^{(n)} = f^{(n)} + g^{(n)} \in D^{1} (A)

according to the sum rule [7.7.4]

So we have: $f + g \in D^{n + 1} (A)$ and

{(f + g)}^{(n + 1)} = (f^{(n)} + g^{(n)})^{'} = (f^{(n)})^{'} + (g^{(n)})^{'} = f^{(n + 1)} + g^{(n + 1)}

Whereas the quotient and the chain rule are too unwieldy to find a sensible result, the product rule fits quite nicely in our rule scheme. Surprisingly this somewhat complex rule, the so called Leibniz rule is exactly shaped like the Generalized Binomial Theorem and thus easy to memorise.

Proposition (Leibniz rule): For all $n \in ℕ^{*}$ we have: $f, g \in D^{n} (A) \Rightarrow f \cdot g \in D^{n} (A)$ and

{(f \cdot g)}^{(n)} = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) f^{(n - i)} \cdot g^{(i)}

[7.8.18]

Proof by induction:

The base step is in fact provided by the product rule [7.7.6]: If $f, g \in D^{1} (A)$ the product $f \cdot g$ is a $D^{1}$ -function as well and (note that both binomial coefficients are of value 1):

$(f \cdot g)^{'} = f^{'} \cdot g + f \cdot g^{'} = \sum_{i = 0}^{1} (\begin{matrix} 1 \\ i \end{matrix}) f^{(1 - i)} \cdot g^{(i)}$
Now let the Leibniz rule be valid for a fixed n. If f and g are two $D^{n + 1}$ -functions, i.e.

$f, g \in D^{n} (A)$ and $f^{(i)}, g^{(i)} \in D^{1} (A)$ for all $i \leq n$ ,

the induction hypothesis guarantees that $f \cdot g$ is a $D^{n}$ -function with

${(f \cdot g)}^{(n)} = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) \underset{\in D^{1} (A)}{\underset{︸}{f^{(n - i)}}} \cdot \underset{\in D^{1} (A)}{\underset{︸}{g^{(i)}}}$

As this derivative is differentiable again according to the product and sum rule we have: $f \cdot g \in D^{n + 1} (A)$ . To calculate the final derivative we use the induction hypothesis, the "index shift" trick and a certain sum rule for the binomial coefficients:

$\begin{array}{l} {(f + g)}^{(n + 1)} & = ({(f + g)}^{(n)})^{'} \\ = (\sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) f^{(n - i)} \cdot g^{(i)})^{'} \\ = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) (f^{(n + 1 - i)} \cdot g^{(i)} + f^{(n - i)} \cdot g^{(i + 1)}) \\ = \sum_{i = 0}^{n} (\begin{matrix} n \\ i \end{matrix}) f^{(n + 1 - i)} \cdot g^{(i)} + \sum_{i = 1}^{n + 1} (\begin{matrix} n \\ i - 1 \end{matrix}) f^{(n - (i - 1))} \cdot g^{(i)} \\ = (\begin{matrix} n \\ 0 \end{matrix}) f^{(n + 1)} \cdot g^{(0)} + \sum_{i = 1}^{n} ((\begin{matrix} n \\ i \end{matrix}) + (\begin{matrix} n \\ i - 1 \end{matrix})) f^{(n + 1 - i)} \cdot g^{(i)} + (\begin{matrix} n \\ n \end{matrix}) f^{(0)} \cdot g^{(n + 1)} \\ = (\begin{matrix} n + 1 \\ 0 \end{matrix}) f^{(n + 1)} \cdot g^{(0)} + \sum_{i = 1}^{n} (\begin{matrix} n + 1 \\ i \end{matrix}) f^{(n + 1 - i)} \cdot g^{(i)} + (\begin{matrix} n + 1 \\ n + 1 \end{matrix}) f^{(0)} \cdot g^{(n + 1)} \\ = \sum_{i = 0}^{n + 1} (\begin{matrix} n + 1 \\ i \end{matrix}) f^{(n + 1 - i)} \cdot g^{(i)} \end{array}$

With the above results we now see that the groups and rings we found at the end of 7.7. are only special cases of a more general situation:

$(D^{n} (A), +)$ , $(C^{n} (A), +)$ and $(C^{\infty} (A), +)$ are abelian groups
i

The addition + is associative and commutative.

0 is the neutral element, i.e. $f + 0 = f$ for all f.

Each f has a unique inverse, $- f$ in this case, such that $f + (- f) = 0$ .

.

$(D^{n} (A), +, \cdot)$ , $(C^{n} (A), +, \cdot)$ and $(C^{\infty} (A), +, \cdot)$ are commutative rings with identity element
i

The axioms for an abelian group are satisfied.

The multiplication · is associative and commutative.

· is distributive with respect to +.

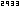1 is the neutral element for the multiplication, i.e. $1 \cdot f = f$ for all f.

.

7.7. 7.9.