9.7. Affine Unterräume

Mit Hilfe von Untervektorräumen konnten wir beliebige Ursprungsgeraden, Ursprungsebenen usw. des ${\displaystyle {ℝ}^n}$ darstellen. Eine "gewöhnliche" Gerade etwa, die den Nullvektor 0 nicht enthält, ist kein Untervektorraum. Mit den bisherigen Mitteln läßt sie sich also nicht beschreiben.

Andererseits findet man unter ihren Parallelen (genau!) eine Ursprungsgerade, so dass wir sie als eine verschobene Urpsrungsgerade auffassen können. Wir erreichen eine solche Verschiebung, indem wir zu jedem Vektor der Ursprungsgeraden einen festen Verschiebevektor aufaddieren. Die folgende Definition setzt diesen Gedanken um.
 

Definition:  Es sei V ein Vektorraum, ${\displaystyle W\subset V}$ ein Untervektorraum und ${\displaystyle a\in V}$. Dann heißt die Menge ${\displaystyle a+W=\{a+w|w\in W\}}$ ein affiner Unterraum (oder auch eine lineare Mannigfaltigkeit) von V. Dabei heißt a Aufpunkt (oder auch Ortsvektor) von ${\displaystyle a+W}$. W zugrundeliegender Raum von ${\displaystyle a+W}$. Ist speziell ${\displaystyle W=<v_1,\dots ,v_n>}$, so heißen die Vektoren ${\displaystyle v_1,\dots ,v_n}$ die Richtungsvektoren von ${\displaystyle a+W}$. Wir setzen die Dimension eines affinen Unterraums fest durch: ${\displaystyle \dim a+W=\dim W}$. Einige Sonderfälle werden sprachlich unterschieden: ${\displaystyle a+W}$ ist ein Punkt, falls ${\displaystyle \dim W=0}$, eine Gerade, falls ${\displaystyle \dim W=1}$, eine Ebene, falls ${\displaystyle \dim W=2}$, eine Hyperebene, falls V endlich und ${\displaystyle \dim W=\dim V-1}$ ist.

Beachte:

Die Zugehörigkeit eines Vektors zu einem affinen Unterraum ist eng gekoppelt mit der Zugehörigkeit zum zugrundeliegenden Raum. Die beiden folgenden Äquivalenzen sind leicht einzusehen; wir werden sie häufig einsetzen:

• ${\displaystyle w\in W\iff a+w\in a+W}$.
• ${\displaystyle x\in a+W\iff x-a\in W}$.

Der zugrundeliegende Raum eines affinen Unterraums ist eindeutig bestimmt! Wir können also von dem zugrundeliegenden Raum sprechen; ebenso ist der oben eingeführte Dimensionsbegriff erst dadurch sauber gefasst.
 

Bemerkung:  Es sei ${\displaystyle a+W}$ ein affiner Unterraum von V und ${\displaystyle W^{\ast }\subset V}$ ein Untervektorraum. Dann gilt: ${\displaystyle a+W=a+W^{\ast }\iff W=W^{\ast }}$. Für den Beweis reicht es offensichtlich, diese Richtung "${\displaystyle \Rightarrow }$" nachzuweisen. Die Äquivalenz ${\displaystyle w\in W\iff a+w\in a+W\iff a+w\in a+W^{\ast }\iff w\in W^{\ast }}$ zeigt aber, dass ${\displaystyle W}$ und ${\displaystyle W^{\ast }}$ dieselben Elemente enthalten.

 Wir üben den neuen Begriff an einigen Beispielen:

Beispiel:  ${\displaystyle \left(\begin{array}{c}1\\ 2\\ 0\\ 1\end{array}\right)+<\mathbf{0}>=\{\left(\begin{array}{c}1\\ 2\\ 0\\ 1\end{array}\right)\}}$ ist ein Punkt in ${\displaystyle {ℝ}^4}$. Der Nullvektor ist Richtungsvektor und ${\displaystyle \left(\begin{array}{c}1\\ 2\\ 0\\ 1\end{array}\right)}$ ein Aufpunkt.   ${\displaystyle \left(\begin{array}{c}3\\ 1\end{array}\right)+<\left(\begin{array}{c}1\\ 1\end{array}\right)>=\{\left(\begin{array}{c}3+\alpha \\ 1+\alpha \end{array}\right)|\alpha \in ℝ\}}$ ist eine Gerade in ${\displaystyle {ℝ}^2}$ mit ${\displaystyle \left(\begin{array}{c}1\\ 1\end{array}\right)}$ als Richtungsvektor und ${\displaystyle \left(\begin{array}{c}3\\ 1\end{array}\right)}$ als einem Aufpunkt.   ${\displaystyle \left(\begin{array}{c}0\\ 3\\ 0\end{array}\right)+<\left(\begin{array}{c}0\\ -1\\ 1\end{array}\right),\left(\begin{array}{c}3\\ -2\\ 0\end{array}\right)>=\{\left(\begin{array}{c}3\beta \\ 3-\alpha -2\beta \\ \alpha \end{array}\right)|\alpha ,\beta \in ℝ\}}$ ist eine Ebene in ${\displaystyle {ℝ}^3}$. ${\displaystyle \left(\begin{array}{c}0\\ 3\\ 0\end{array}\right)}$ ist ein Aufpunkt und ${\displaystyle \left(\begin{array}{c}0\\ -1\\ 1\end{array}\right),\left(\begin{array}{c}3\\ -2\\ 0\end{array}\right)}$ sind die Richtungsvektoren.   ${\displaystyle 5+<\mathrm{X},{\mathrm{X}}^2>=\{p|p\text{ist Polynom vom}grad\le \mathrm{2,}\text{das die}y\text{-Achse in 5 schneidet}\}}$ ist eine Ebene in ${\displaystyle {\mathbb{P}}^2}$. ${\displaystyle {\mathrm{X}}^2,\mathrm{X}}$ sind die Richtungsvektoren und 5 ist ein Aufpunkt.   ${\displaystyle 3{\mathrm{X}}^4-2\mathrm{X}+<e^{2\mathrm{X}},e^{-4\mathrm{X}}>}$ ist eine Ebene in ${\displaystyle 𝔽(ℝ)}$. Das Polynom ${\displaystyle 3{\mathrm{X}}^4-2\mathrm{X}}$ ist dabei ein Aufpunkt und die Funktionen ${\displaystyle e^{2\mathrm{X}},e^{-4\mathrm{X}}}$ sind die Richtungsvektoren.   Jeder Untervektorraum ${\displaystyle W\subset V}$ ist ein affiner Unterraum von V, denn: ${\displaystyle W=\mathbf{0}+W}$. Die Berechnungen in den ersten drei Beispielen lassen sich natürlich auch umkehren: ${\displaystyle \{\left(\begin{array}{c}3+\alpha \\ 2\\ -2\alpha \end{array}\right)|\alpha \in ℝ\}?=\left(\begin{array}{c}3\\ 2\\ 0\end{array}\right)+<\left(\begin{array}{c}1\\ 0\\ -2\end{array}\right)>\text{.}}$   ${\displaystyle \{\left(\begin{array}{c}2\alpha +4\beta \\ 4+\alpha +2\beta \\ 1-\alpha -2\beta \end{array}\right)|\alpha ,\beta \in ℝ\}?=\left(\begin{array}{c}0\\ 4\\ 1\end{array}\right)+<\left(\begin{array}{c}2\\ 1\\ -1\end{array}\right),\left(\begin{array}{c}4\\ 2\\ -2\end{array}\right)>=\left(\begin{array}{c}0\\ 4\\ 1\end{array}\right)+<\left(\begin{array}{c}2\\ 1\\ -1\end{array}\right)>\text{.}}$

Die beiden folgenden Beispiele machen einige affine Unterräume sichtbar:

Beispiel: Im folgenden Applet können (null- und) eindimensionale affine Unterräume des ${\displaystyle {ℝ}^2}$, also die Mengen der Form ${\displaystyle M=\mathit{a}+<\mathit{v}>}$ mit Hilfe der Maus graphisch erzeugt werden. Neben der zeichnerischen Darstellung wird M sowohl in der dieser Form angegeben als auch als Lösungsmenge eines linearen Gleichungssystems (vgl. Kapitel 9_9). Den Aufpunkt a (rot) setzt man durch Klicken in die Zeichenebene. Der Richtungsvektor v (blau) kann durch Ziehen der Spitze verändert werden.

 

Beispiel: Die (ein- und) zweidimensionalen affinen Unterräume des ${\displaystyle {ℝ}^3}$, also die Mengen der Form ${\displaystyle M=\mathit{a}+<{\mathit{v}}_1,{\mathit{v}}_2>}$ lassen sich nur mit persektivischen Tricks darstellen. Im nachfolgenden Applet kann man den affinen Unterraum M durch Variieren der Blickwinkel phi und theta von verschiedenen Seiten betrachten. 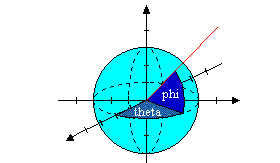Die Erzeuger v1 und v2 haben (ohne Einschränkung) die Länge 1; sie werden über die beiden rechten Halbkugeln gewählt. Die Richtung des Aufpunkts a wird über die linke Halbkugel eingestellt. Zuvor kann man über die Schieberleiste einen Streckungsfaktor (von -6 bis 6) wählen. Ist die checkbox Aufpunkt aktiviert, so wird Position des Aufpunkts durch zusätzliche Hilfslinien verdeutlicht. Alle Einstellungen werden durch Klicken oder Ziehen vorgenommen. Die Achsen sind in Einerschritten markiert.

Kehren wir nun zurück zu den allgemeinen Eigenschaften. Zunächst erhalten wir ein oft nützliches Ergebnis: Aufpunkte von affinen Unterräume sind austauschbar! Allerdings darf man dazu nur Vektoren aus demselben affinen Unterraum  nehmen.
 

Bemerkung:  ${\displaystyle M=a+W}$ sei ein affiner Unterraum in V. Dann gilt: ${\displaystyle a\in M}$. ${\displaystyle x,y\in M\Rightarrow x-y\in W}$. ${\displaystyle M=b+W\text{für alle}b\in M}$. Beweis: Zu 1.: ${\displaystyle a=a+\mathbf{0}\text{und}\mathbf{0}\in W}$. Zu 2.: Sind x und  y Vektoren aus M, so besitzen sie eine dem entsprechende Darstellung; es gibt also ${\displaystyle w,w^{\ast }\in W}$, so dass ${\displaystyle \begin{array}{l}x=a+w\hfill \\ y=a+w^{\ast }\hfill \end{array}}$ Weil nun W ein Untervektoraum ist, hat man: ${\displaystyle x-y=a+w-(a+w^{\ast })=w-w^{\ast }\in W}$. Zu 3.: Sei b ein beliebiger Vektor aus M. Wir zeigen wieder, dass M und ${\displaystyle b+W}$ dieselben Elemente enthalten: ${\displaystyle \begin{array}{ll}x\in M\hfill & \iff x-a\in W\hfill \\ \hfill & \iff x-b+(b-a)\in W\hfill \\ \hfill & \iff x-b\in W,\text{denn nach1}\text{. und 2}\text{. ist}b-a\in W\hfill \\ \hfill & \iff x\in b+W\text{.}\hfill \end{array}}$

Die nächste Bemerkung stellt eine zentrale Konstruktionsmethode für affine Unterräume vor. Wir verallgemeinern dabei das bekannte Prinzip "eine Gerade bereits durch zwei (verschiedene) Punkte eindeutig bestimmt" zu: 

Affine Unterräume können also maßgeschneidert werden.

Bemerkung:  Sind ${\displaystyle v_0,\dots ,v_n\in Vn+1}$ viele Vektoren aus V, so ist ${\displaystyle v_0+<v_1-v_0,\dots ,v_n-v_0>}$ der kleinste affine Unterraum von V, der ${\displaystyle v_0,v_1,\dots ,v_n}$ enthält. Beweis: Zunächst gehört der Aufpunkt ${\displaystyle v_0}$ zu ${\displaystyle v_0+<v_1-v_0,\dots ,v_n-v_0>}$. Die restlichen Vektoren ${\displaystyle v_1,\dots ,v_n}$ lassen die Darstellung ${\displaystyle v_i=v_0+\sum _{j=1}^n{\delta }_{i,j}(v_j-v_0)}$ zu und gehören somit ebenfalls zu ${\displaystyle v_0+<v_1-v_0,\dots ,v_n-v_0>}$. Sei nun ${\displaystyle M=a+W}$ ein ein weiterer affiner Unterraum, der auch die Vektoren ${\displaystyle v_0,v_1,\dots ,v_n}$ enthält. Wir müssen zeigen:  ${\displaystyle v_0+<v_1-v_0,\dots ,v_n-v_0>\subset M}$. Zunächst tauschen wir den Aufpunkt von M aus, denn da ${\displaystyle v_0\in M}$, ist ${\displaystyle M=v_0+W}$. Nun argumentieren wir folgendermaßen: Da Differenzen von Vektoren aus M in W liegen, hat man: ${\displaystyle \begin{array}{ll}{v}_1-v_0,\dots ,v_n-v_0\in W\hfill & \Rightarrow <v_1-v_0,\dots ,v_n-v_0>\subset W\hfill \\ \hfill & \Rightarrow v_0+<v_1-v_0,\dots ,v_n-v_0>\subset v_0+W=M\text{.}\hfill \end{array}}$

 

Beispiel: ${\displaystyle \left(\begin{array}{c}3\\ 2\end{array}\right)+<\left(\begin{array}{c}1\\ 7\end{array}\right)-\left(\begin{array}{c}3\\ 2\end{array}\right)>=\left(\begin{array}{c}3\\ 2\end{array}\right)+<\left(\begin{array}{c}-2\\ 5\end{array}\right)>}$ ist der kleinste affine Unterraum von ${\displaystyle {ℝ}^2}$, der durch ${\displaystyle \left(\begin{array}{c}3\\ 2\end{array}\right)}$ und ${\displaystyle \left(\begin{array}{c}1\\ 7\end{array}\right)}$ geht.   ${\displaystyle \left(\begin{array}{c}2\\ 0\\ 2\end{array}\right)+<\left(\begin{array}{c}3\\ 1\\ 4\end{array}\right)-\left(\begin{array}{c}2\\ 0\\ 2\end{array}\right),\left(\begin{array}{c}7\\ 4\\ 4\end{array}\right)-\left(\begin{array}{c}2\\ 0\\ 2\end{array}\right)>=\left(\begin{array}{c}2\\ 0\\ 2\end{array}\right)+<\left(\begin{array}{c}1\\ 1\\ 2\end{array}\right),\left(\begin{array}{c}5\\ 4\\ 2\end{array}\right)>}$ ist der kleinste affine Unterraum von ${\displaystyle {ℝ}^3}$, der durch ${\displaystyle \left(\begin{array}{c}2\\ 0\\ 2\end{array}\right),\left(\begin{array}{c}3\\ 1\\ 4\end{array}\right)}$ und ${\displaystyle \left(\begin{array}{c}7\\ 4\\ 4\end{array}\right)}$ geht.   ${\displaystyle \left(\begin{array}{c}6\\ 3\end{array}\right)+<\left(\begin{array}{c}7\\ 3\end{array}\right)-\left(\begin{array}{c}6\\ 3\end{array}\right),\left(\begin{array}{c}6\\ 4\end{array}\right)-\left(\begin{array}{c}6\\ 3\end{array}\right),\left(\begin{array}{c}8\\ 8\end{array}\right)-\left(\begin{array}{c}6\\ 3\end{array}\right)>=\left(\begin{array}{c}6\\ 3\end{array}\right)+<\left(\begin{array}{c}1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 1\end{array}\right),\left(\begin{array}{c}2\\ 5\end{array}\right)>={ℝ}^2}$ ist der kleinste affine Unterraum von ${\displaystyle {ℝ}^2}$, der durch ${\displaystyle \left(\begin{array}{c}6\\ 3\end{array}\right),\left(\begin{array}{c}7\\ 3\end{array}\right),\left(\begin{array}{c}6\\ 4\end{array}\right)}$ und ${\displaystyle \left(\begin{array}{c}8\\ 8\end{array}\right)}$ geht.   ${\displaystyle \left(\begin{array}{c}3\\ 1\end{array}\right)+<\varnothing >=\{\left(\begin{array}{c}3\\ 1\end{array}\right)\}}$ ist der kleinste affine Unterraum von ${\displaystyle {ℝ}^2}$, der durch ${\displaystyle \left(\begin{array}{c}3\\ 1\end{array}\right)}$ geht.   ${\displaystyle \sin +<\mathrm{X}-\sin ,\cos -\sin >}$ ist der kleinste affine Unterraum von ${\displaystyle 𝔽(ℝ)}$, der durch ${\displaystyle \sin ,\mathrm{X}\text{und}\cos }$ geht.

 

Aufgabe:  Berechne den kleinsten affinen Unterraum M von ${\displaystyle {ℝ}^4}$, der durch ${\displaystyle \left(\begin{array}{c}6\\ 3\\ 1\\ 1\end{array}\right),\left(\begin{array}{c}2\\ 0\\ 1\\ 0\end{array}\right),\left(\begin{array}{c}1\\ 3\\ 3\\ 1\end{array}\right)}$ geht:   ${\displaystyle M=?\left(\begin{array}{c}6\\ 3\\ 1\\ 1\end{array}\right)+<\left(\begin{array}{c}2\\ 0\\ 1\\ 0\end{array}\right)-\left(\begin{array}{c}6\\ 3\\ 1\\ 1\end{array}\right),\left(\begin{array}{c}1\\ 3\\ 3\\ 1\end{array}\right)-\left(\begin{array}{c}6\\ 3\\ 1\\ 1\end{array}\right)>=\left(\begin{array}{c}6\\ 3\\ 1\\ 1\end{array}\right)+<\left(\begin{array}{c}-4\\ -3\\ 0\\ -1\end{array}\right),\left(\begin{array}{c}-5\\ 0\\ 2\\ 0\end{array}\right)>\text{.}}$   von ${\displaystyle {ℝ}^3}$, der durch ${\displaystyle \left(\begin{array}{c}2\\ 0\\ 1\end{array}\right),\left(\begin{array}{c}5\\ -4\\ 3\end{array}\right),\left(\begin{array}{c}-4\\ 8\\ -3\end{array}\right)}$ geht:  ${\displaystyle M=?\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right)+<\left(\begin{array}{c}5\\ -4\\ 3\end{array}\right)-\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right),\left(\begin{array}{c}-4\\ 8\\ -3\end{array}\right)-\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right)>=\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right)+<\left(\begin{array}{c}3\\ -4\\ 2\end{array}\right),\left(\begin{array}{c}-6\\ 8\\ -4\end{array}\right)>=\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right)+<\left(\begin{array}{c}3\\ -4\\ 2\end{array}\right)>\text{.}}$   von ${\displaystyle 𝔽(ℝ)}$, der durch ${\displaystyle 3{\mathrm{X}}^2\text{und}{\mathrm{X}}^2}$ geht:  ${\displaystyle M=?3{\mathrm{X}}^2+<3{\mathrm{X}}^2-{\mathrm{X}}^2>=3{\mathrm{X}}^2+<2{\mathrm{X}}^2>=<{\mathrm{X}}^2>\text{.}}$

In einem der ersten Beispiele sind Untervektorräume als spezielle affine Unterräume erkannt worden. Die nachfolgende Bemerkung stellt einige Kriterien zusammen, die diesen Sonderfall ausmachen.

Bemerkung:  Für einen affinen Unterraum ${\displaystyle M=a+W}$ von V sind die folgenden Aussagen äquivalent: M ist ein Vektorraum ${\displaystyle \mathbf{0}\in M}$ ${\displaystyle a\in W}$ ${\displaystyle M=W}$ Beweis: 1.${\displaystyle \Rightarrow }$2.: Hier ist nichts zu zeigen. 2.${\displaystyle \Rightarrow }$3.: Es gibt also ein ${\displaystyle w\in W}$, so dass ${\displaystyle \mathbf{0}=a+w}$. Folgt: ${\displaystyle a=-w\in W}$. 3.${\displaystyle \Rightarrow }$4.: Mit ${\displaystyle a}$ ist auch ${\displaystyle -a\in W}$, also hat man: ${\displaystyle \mathbf{0}=a+(-a)\in M}$. Man kann somit den Aufpunkt von M austauschen: ${\displaystyle M=\mathbf{0}+W=W}$. 4.${\displaystyle \Rightarrow }$1.: Hier ist wieder nichts zu zeigen.

Treffen zwei affine Unterräume aufeinander, so führt lediglich die Schnittbildung nicht aus der Klasse der affinen Unterräume heraus.

Bemerkung:  ${\displaystyle M=a+W}$ und ${\displaystyle N=a^{\ast }+W^{\ast }}$ seien zwei affine Unterräume von V. Ist ${\displaystyle M\cap N\ne \varnothing }$, so ist ${\displaystyle M\cap N}$ wieder ein affiner Unterraum von V. Beweis: Sei b ein gemeinsamer Vektor von M und N. Wir können b sowohl bei M als auch bei N als neuen Aufpunkt einsetzen: ${\displaystyle \begin{array}{l}M=b+W\hfill \\ N=b+W^{\ast }\hfill \end{array}}$ Nun zeigen wir: ${\displaystyle M\cap N=b+W\cap W^{\ast }}$. Da ${\displaystyle W\cap W^{\ast }}$ ein Untervektorraum ist, ist durch diese Gleichheit die Aussage bewiesen. ${\displaystyle \begin{array}{ll}x\in M\cap N\hfill & \iff x\in M\wedge x\in N\hfill \\ \hfill & \iff x-b\in W\wedge x-b\in W^{\ast }\hfill \\ \hfill & \iff x-b\in W\cap W^{\ast }\hfill \\ \hfill & \iff x\in b+W\cap W^{\ast }\text{.}\hfill \end{array}}$

Zur effektiven Berechnung des Schnittraums ${\displaystyle M\cap N}$ werden wir allerdings erst dann kommen, wenn wir ein sicheres Verfahren zur Lösung linearer Gleichungssysteme entwickelt haben. Dies ist u.a. Aufgabe des nächsten Abschnitts. Hier charakterisieren wir zunächst die möglichen Lagebeziehungen zweier affiner Unterräume zu einander:
 

Definition:  ${\displaystyle M=a+W}$ und ${\displaystyle N=a^{\ast }+W^{\ast }}$ seien zwei affine Unterräume von V. Wir sagen: ${\displaystyle W\subset W^{\ast }\vee W^{\ast }\subset W}$. M und N sind echt parallel, falls sie parallel sind und ${\displaystyle M\cap N=\varnothing }$. M und N sind windschief, falls sie nicht parallel sind und ${\displaystyle M\cap N=\varnothing }$.

Die Bedeutung der affinen Unterräume ist nicht auf den geometrischen Bereich beschränkt. Bei einer wichtigen Methode zur Konstruktion neuer Vektorräume, der sog. Quotientenräume, übernehmen sie die Rolle der neuen Vektoren!

 

Definition:  Es sei V ein Vektorraum und ${\displaystyle W\subset V}$ ein Untervektorraum. Dann heißt die Menge   ${\displaystyle V_{{/}_W}=\{a+W|a\in V\}}$ der Quotientenraum von V nach W. Die Elemente von ${\displaystyle V_{{/}_W}}$ werden in diesem Zusammenhang auch Nebenklassen von W genannt.

Beachte:
Da die Aufpunkte affiner Unterräume austauschbar sind, kann ein Element von ${\displaystyle V_{{/}_W}}$ verschiedene Darstellungsformen haben. Entscheidend ist in diesem Zusammenhang die folgende Äquivalenz:
 

Die Quotientenräume von V "erben" auf natürliche Weise eine Vektorraumstruktur. Wir führen zunächst eine Addition und eine Skalarenmultiplikation ein:
 

Definition und Bemerkung:  ${\displaystyle a+W}$ und ${\displaystyle b+W}$ Elemente von ${\displaystyle V_{{/}_W}}$ und ${\displaystyle \alpha \in ℝ}$, so setzen wir: ${\displaystyle (a+W)+(b+W)=(a+b)+W}$ ${\displaystyle \alpha (a+W)=(\alpha a)+W}$ Die so eingeführte Addition und die skalare Multiplikation hängen nicht von der speziellen Darstellung der Elemente ab, sie sind vertreterunabhängig definiert. Hat man nämlich ${\displaystyle a+W=a\mathit{\text{'}}+W}$ und ${\displaystyle b+W=b\mathit{\text{'}}+W}$, also: ${\displaystyle a-a\mathit{\text{'}}\in W}$ und ${\displaystyle b-b\mathit{\text{'}}\in W}$, so gilt: ${\displaystyle a+b-(a\mathit{\text{'}}+b\mathit{\text{'}})=a-a\mathit{\text{'}}+b-b\mathit{\text{'}}\in W}$, d.h.aber: ${\displaystyle (a+b)+W=(a\mathit{\text{'}}+b\mathit{\text{'}})+W}$. ${\displaystyle \alpha a-\alpha a\mathit{\text{'}}=\alpha (a-a\mathit{\text{'}})\in W}$, also: ${\displaystyle (\alpha a)+W=(\alpha a\mathit{\text{'}})+W}$.

 

Bemerkung:  Es sei V ein Vektorraum und ${\displaystyle W\subset V}$ ein Untervektorraum. Mit den zuvor eingeführten Rechenoperationen + und · gilt:   ${\displaystyle (V_{{/}_W},+,\cdot )}$ ist ein Vektorraum. Beweis: Wir überprüfen die 8 definierenden Eigenschaften, wobei wir auf die entsprechen Eigenschaften in ${\displaystyle (V,+,\cdot )}$ zurückgreifen: + ist assoziativ: ${\displaystyle \begin{array}{ll}\hfill & ((a+W)+(b+W))+(c+W)\hfill \\ =\hfill & ((a+b)+c)+W\hfill \\ =\hfill & (a+(b+c))+W\hfill \\ =\hfill & (a+W)+((b+W)+(c+W))\text{.}\hfill \end{array}}$.   + ist kommutativ: ${\displaystyle \begin{array}{ll}\hfill & (a+W)+(b+W)\hfill \\ =\hfill & (a+b)+W\hfill \\ =\hfill & (b+a)+W\hfill \\ =\hfill & (b+W)+(a+W)\hfill \end{array}}$.   Es gibt ein neutrales Element 0 bzgl. +, und zwar ist dies ${\displaystyle \mathbf{0}+W=W}$: ${\displaystyle (\mathbf{0}+W)+(a+W)=(\mathbf{0}+a)+W=a+W}$.   Jedes Element ${\displaystyle a+W}$ besitzt ein inverses Element, nämlich ${\displaystyle -a+W}$: ${\displaystyle (a+W)+(-a+W)=(a+(-a))+W=\mathbf{0}+W=W}$.   ${\displaystyle \alpha (\beta (a+W))=\alpha (\beta a+W)=\alpha (\beta a)+W=(\alpha \beta )a+W=(\alpha \beta )(a+W)}$.   ${\displaystyle 1(a+W)=1a+W=a+W}$.   ${\displaystyle \begin{array}{ll}\hfill & (\alpha +\beta )(a+W)\hfill \\ =\hfill & (\alpha +\beta )a+W\hfill \\ =\hfill & (\alpha a+\beta a)+W\hfill \\ =\hfill & (\alpha a+W)+(\beta a+W)\hfill \\ =\hfill & \alpha (a+W)+\beta (a+W)\text{.}\hfill \end{array}}$   ${\displaystyle \begin{array}{ll}\hfill & \alpha ((a+W)+(b+W))\hfill \\ =\hfill & \alpha ((a+b)+W)\hfill \\ =\hfill & \alpha (a+b)+W\hfill \\ =\hfill & (\alpha a+\alpha b)+W\hfill \\ =\hfill & (\alpha a+W)+(\alpha b+W)\hfill \\ =\hfill & \alpha (a+W)+\alpha (b+W)\text{.}\hfill \end{array}}$

Das folgende allgemeine Beispiel beschreibt die Rolle des kleinsten, bzw. des größten Untervektorraums bei der Quotientenbildung.
 

Beispiel:  V sei ein beliebiger Vektorraum; dann gilt: ${\displaystyle V_{{/}_{\{\mathbf{0}\}}}=\{a+\{0\}|a\in V\}=\{\{a\}|a\in V\}}$ ist also die Menge der Punkte in V. ${\displaystyle V_{{/}_V}=\{a+V|a\in V\}=\{V\}=\{0\}}$. ${\displaystyle V_{{/}_V}}$ ist stets der Nullraum.

Es gibt natürlich auch "richtige" Beispiele:
 

Beispiel: ${\displaystyle {{ℝ}^3}_{{/}_{<{\mathit{e}}_3>}}=\{\mathit{a}+<{\mathit{e}}_3>|\mathit{a}\in {ℝ}^3\}=\{\left(\begin{array}{c}{a}_1\\ a_2\\ 0\end{array}\right)+<{\mathit{e}}_3>|\mathit{a}\in {ℝ}^2\}}$   ${\displaystyle {{\mathbb{P}}^2}_{{/}_{<{\mathrm{X}}^2>}}=\{p+<{\mathrm{X}}^2>|p\in {\mathbb{P}}^2\}=\{q+<{\mathrm{X}}^2>|q\in {\mathbb{P}}^1\}}$

9.6

9.8.