Beispiel einer lokal nicht injektiven, regulären Funktion

Die Funktion  ${\displaystyle f:ℝ\to ℝ}$ sei gegeben durch ${\displaystyle f(x)≔\{\begin{array}{l}x+x^2\cos \frac{\mathrm{\pi }}{x}\text{ , falls }x\ne 0\hfill \\ 0\text{ , falls }x=0\hfill \end{array}}$

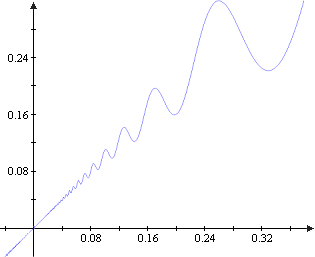
f ist eine Beispielfunktion der gesuchten Art. Genauer zeigen wir nämlich:

1. f ist in 0 differenzierbar mit  ${\displaystyle f^{\prime }(0)=1}$.

2. f ist in keiner Umgebung von 0 injektiv.

Beweis:  

1. ►  Aus der für alle ${\displaystyle x\ne 0}$ gültigen Ungleichung

folgt aus dem Schachtelsatz [6.9.10] zunächst ${\displaystyle \underset{x\to 0}{\lim }|m_0(x)-1|=0}$ und mit [6.9.11] dann auch die Behauptung ${\displaystyle \underset{x\to 0}{\lim }{m}_0(x)=1}$.

2. ►  f ist stetig (in 0 als Folge von 1. und in ${\displaystyle x\ne 0}$ aufgrund der Rechenregeln für stetige Funktionen). Wir betrachten nun für ein beliebiges ${\displaystyle k\in {\mathbb{N}}^{\ast }}$ die Zahlen

und zeigen dann

Nach Zwischenwertsatz ([6.6.2]) existiert dann ein ${\displaystyle \tilde{x}\in ]\frac{1}{2k+1},\frac{1}{2k}[}$, also insbesondere ${\displaystyle \tilde{x}\ne \frac{1}{2k+2}}$, mit  ${\displaystyle f(\tilde{x})=f(\frac{1}{2k+2})}$. Das bedeutet aber:  f ist in ${\displaystyle ]-\frac{1}{2k},\frac{1}{2k}[}$ nicht injektiv.

Zum Nachweis von [1] und [2] beachte man, dass der Cosinus an den geraden Vielfachen von π den Wert 1, und an den ungeraden den Wert −1 annimmt. Es ist daher

Der Nachweis von [1] ergibt sich daher durch die folgende Rechnung:

[2] bestätigt man auf die gleiche Weise: