Beweis: Wir verwenden den Weierstraßschen Approximationssatz (für einen alternativen ad-hoc Beweis hier klicken). Nach [6.7.2] gibt es eine Folge von Polynomen , die auf gleichmäßig gegen f konvergiert:
Nach [8.1.10] ist jedes Polynom integrierbar. Also besitzt der gleichmäßige Limes f eine Stammfunktion gemäß [8.1.15].
Beweis: Wir konstruieren zu jedem einen Polygonzug (ein kürzerer Beweis greift direkt auf die Bernsteinpolynome zurück) indem wir geeignete Graphenpunkte von f durch einen Streckenzug verbinden. Dazu zerlegen wir das Intervall in n Teilintervalle der Länge , und setzen für
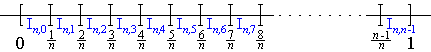
Mit den Eckpunkten der Teilungsintervalle haben wir gleichzeitig Graphenpunkte von f ausgezeichnet. Den i-ten verbinden wir mit dem ()-ten durch die Strecke
wobei die Steigung durch den Quotienten
gegeben ist. Für ist und
,
so dass wir den gesuchten Polygonzug als wohldefinierte
Verklebung
i  |
|
Für und mit für alle ist
|
gewinnen können. Ein aufrufbares
Applet
i  |
|
|
zeigt am Beispiel der Funktion , wie die Folge der Polygonzüge die Funktion f approximiert.
Als Einschränkung einer linearen Funktion ist jede Strecke integrierbar (siehe [8.1.10], [8.1.13]). [8.1.14] sichert damit die Integrierbarkeit von und [8.1.15] folglich die von f, wenn wir die gleichmäßige Konvergenz
zeigen können. Seien dazu und beliebig. Da f auf dem geschlossenem Intervall gleichmäßig stetig ist, gibt es ein , so dass alle die Folgerung
erfüllen. Für ein beliebiges wenden wir diesen Schluss zweimal an:
-
Da lassen sich die Steigungen der Verbindungsstrecken abschätzen:
für alle
.
-
x liegt in einem der Intervalle , etwa . Man hat daher und , d.h. also: