mathproject >> 8.3. Integration by Parts and Substitution Formula

Theorem (integration by parts): Let f and g be two differentiable functions on I, i.e

f, g \in D^{1} (I)

. Then the following holds:

If $f^{'} \cdot g$ is integrable on I then $f \cdot g^{'}$ is integrable as well and for all $a, b \in I$ we have:

\int_{a}^{b} f \cdot g^{'} = f \cdot g |_{a}^{b} - \int_{a}^{b} f^{'} \cdot g

[8.3.1]

Proof: With the product rule [7.7.6] we find that $f \cdot g$ is differentiable on I and that $(f \cdot g)^{'} = f^{'} \cdot g + f \cdot g^{'}$ . In other words: $f^{'} \cdot g + f \cdot g^{'}$ has a primitive, namely $f \cdot g$ . Now, if $f^{'} \cdot g$ is integrable the same is true for $f \cdot g^{'} = f^{'} \cdot g + f \cdot g^{'} - f^{'} \cdot g$ due to [8.1.7] and eventually the identity

\int_{a}^{b} f^{'} \cdot g + \int_{a}^{b} f \cdot g^{'} = \int_{a}^{b} f^{'} \cdot g + f \cdot g^{'} = f \cdot g |_{a}^{b}

yields the assertion [8.3.1].

Integration by parts is mainly used for calculating primitives according to the fundamental theorem [8.2.13]. Some examples will explain this technique.

Example:

$- X \cdot \cos + \sin$ is a primitive function of $X \cdot \sin$ as all $x \in ℝ$ satisfy

$\begin{array}{l} \int_{0}^{x} X \cdot \sin & = \int_{0}^{x} X \cdot (- \cos)^{'} \\ = X \cdot (- \cos) |_{0}^{x} - \int_{0}^{x} X^{'} \cdot (- \cos) \\ = - X \cdot \cos |_{0}^{x} + \int_{0}^{x} \cos \\ = - X \cdot \cos |_{0}^{x} + \sin |_{0}^{x} \\ = - x \cdot \cos x + \sin x \end{array}$
$- X^{2} \cdot \cos + 2 X \cdot \sin + 2 \cos$ is a primitive function of $X^{2} \cdot \sin$ : We integrate by parts twice and get for $x \in ℝ$

$\begin{array}{l} \int_{0}^{x} X^{2} \cdot \sin & = \int_{0}^{x} X^{2} \cdot (- \cos)^{'} \\ = X^{2} \cdot (- \cos) |_{0}^{x} + \int_{0}^{x} 2 X \cdot \cos \\ = - X^{2} \cdot \cos |_{0}^{x} + \int_{0}^{x} 2 X \cdot \sin^{'} \\ = - X^{2} \cdot \cos |_{0}^{x} + 2 X \cdot \sin |_{0}^{x} - \int_{0}^{x} 2 \cdot \sin \\ = - X^{2} \cdot \cos |_{0}^{x} + 2 X \cdot \sin |_{0}^{x} + 2 \cos |_{0}^{x} \\ = - x^{2} \cdot \cos x + 2 x \cdot \sin x + 2 \cos x - 2 \end{array}$

and thus know that $- X^{2} \cdot \cos + 2 X \cdot \sin + 2 \cos - 2$ is a primitive of $X^{2} \cdot \sin$ . Finally we omit the constant addend −2.
The last example reveals a primitive of $\cos^{2}$ . The calculation uses Pythagoras' theorem (i.e. the identity $\sin^{2} = 1 - \cos^{2}$ ), a standard trick!

At first we have for $x \in ℝ$ :

$\begin{array}{l} \int_{0}^{x} \cos^{2} = \int_{0}^{x} \cos \cdot \cos & = \int_{0}^{x} \cos \cdot \sin^{'} \\ = \cos \cdot \sin |_{0}^{x} - \int_{0}^{x} \cos^{'} \cdot \sin \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} \sin^{2} \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} 1 - \cos^{2} \\ = \cos \cdot \sin |_{0}^{x} + \int_{0}^{x} 1 - \int_{0}^{x} \cos^{2} \end{array}$

Indeed this is not the expected solution for our integral! Instead however it is an equation satisfied by the unknown integral that could be solved for it:

$\int_{0}^{x} \cos^{2} = \frac{1}{2} (\sin \cdot \cos |_{0}^{x} + \int_{0}^{x} 1) = \frac{1}{2} (\sin x \cdot \cos x + x)$

Finally this proves $\frac{1}{2} (\sin \cdot \cos + X)$ as a primitive of $\cos^{2}$ .

The Pythagorean theorem is often involved when integrating by parts. As another example we prove the recursion formulas for the integrals of $\sin^{n}$ and $\cos^{n}$ .

Proposition: For all $a, b \in ℝ$ and all $n \geq 2$ the following recursions are valid:

$\int_{a}^{b} \sin^{n} = - \frac{\cos \cdot \sin^{n - 1}}{n} \|_{a}^{b} + \frac{n - 1}{n} \int_{a}^{b} \sin^{n - 2}$	[8.3.2]
$\int_{a}^{b} \cos^{n} = \frac{\sin \cdot \cos^{n - 1}}{n} \|_{a}^{b} + \frac{n - 1}{n} \int_{a}^{b} \cos^{n - 2}$	[8.3.3]

Proof: Verification is quite similar in both cases, so it is sufficient to prove only one of them, e.g. 2. From $\sin^{2} = 1 - \cos^{2}$ we get the following equation for $\int_{a}^{b} \cos^{n}$ :

\begin{array}{l} \int_{a}^{b} \cos^{n} = \int_{a}^{b} \sin^{'} \cdot \cos^{n - 1} & = \sin \cdot \cos^{n - 1} |_{a}^{b} - \int_{a}^{b} \sin \cdot (n - 1) \cos^{n - 2} \cdot (- \sin) \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \sin^{2} \cdot \cos^{n - 2} \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} (1 - \cos^{2}) \cdot \cos^{n - 2} \\ = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \cos^{n - 2} - (n - 1) \int_{a}^{b} \cos^{n} \end{array}

Thus we have: $n \int_{a}^{b} \cos^{n} = \sin \cdot \cos^{n - 1} |_{a}^{b} + (n - 1) \int_{a}^{b} \cos^{n - 2}$ which in fact is the assertion.

If a and b are zeros for the sine or for the cosine the recursion formulas could be simplified to

\int_{a}^{b} \sin^{n} = \frac{n - 1}{n} \int_{a}^{b} \sin^{n - 2}

and

\int_{a}^{b} \cos^{n} = \frac{n - 1}{n} \int_{a}^{b} \cos^{n - 2}

In this case we also succeed in finding a non recursive representation. The following integral is needed in [8.5.7] where we will calculate the volume of a sphere.

Proposition: For all $n \geq 0$ we have

\int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} = {\begin{array}{l} \frac{n!}{{(2^{k} k!)}^{2}} \cdot π if n = 2 k \\ \frac{{(2^{k} k!)}^{2}}{n!} \cdot 2 if n = 2 k + 1 \end{array}

[8.3.4]

Proof: The identity [8.3.4] is immediate if $k = 0$ . Without restriction we thus assume that $k > 0$ . If $n = 2 k$ the simplified recursion formula could be applied exactly k times:

\begin{array}{l} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} & = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{1}{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{0} \\ = \frac{n (n - 1)}{n^{2}} \cdot \frac{(n - 2) (n - 3)}{{(n - 2)}^{2}} \cdot \dots \cdot \frac{2 \cdot 1}{2^{2}} \cdot π \\ = \frac{n!}{{((2 k) \cdot (2 k - 2) \cdot \dots \cdot (2 k - 2 (k - 1)))}^{2}} \cdot π \\ = \frac{n!}{(2^{k} {(k \cdot (k - 1) \cdot \dots \cdot (k - (k - 1)))}^{2}} \cdot π & (2 factored out k times) \\ = \frac{n!}{{(2^{k} k!)}^{2}} \cdot π \end{array}

We proceed similar in the case $n = 2 k + 1$ and again apply the simplified recursion formula k times:

\begin{array}{l} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{n} & = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{2}{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{1} \\ = \frac{{(n - 1)}^{2}}{n \cdot (n - 1)} \cdot \frac{{(n - 3)}^{2}}{(n - 2) \cdot (n - 3)} \cdot \dots \cdot \frac{2^{2}}{3 \cdot 2} \cdot 2 \\ = \frac{{((2 k) \cdot (2 k - 2) \cdot \dots \cdot (2 k - 2 (k - 1)))}^{2}}{n!} \cdot 2 \\ = \frac{(2^{k} {(k \cdot (k - 1) \cdot \dots \cdot (k - (k - 1)))}^{2}}{n!} \cdot 2 \\ = \frac{{(2^{k} k!)}^{2}}{n!} \cdot 2 \end{array}

We now turn to the chain rule and its integral version. Different from integration by parts the substitution formula also controls the bounderies of integration.

Theorem (substitution formula): Let I and J be any two intervals and $g : J \to I$ a differentiable function. If f is integrable on I, i.e. $f \in I (I)$ then $(f \circ g) \cdot g^{'} \in I (J)$ and for all $a, b \in J$ the following identity holds:

\int_{a}^{b} (f \circ g) \cdot g^{'} = \int_{g (a)}^{g (b)} f

[8.3.5]

Proof: Let h be a primitive function of f. According to the chain rule ([7.7.8]) the composit $h \circ g$ is differentiable on I and

(h \circ g)^{'} = (h^{'} \circ g) \cdot g^{'} = (f \circ g) \cdot g^{'}

Thus $(f \circ g) \cdot g^{'}$ has $h \circ g$ as a primitive and therefore

\int_{a}^{b} (f \circ g) \cdot g^{'} = (h \circ g) |_{a}^{b} = h |_{g (a)}^{g (b)} = \int_{g (a)}^{g (b)} f

Consider:

Especially with the substitution formula the dx-notation is very common. In this world however it is not only the identity's differential dx that has to be considered but also the differential

d g (x) = g^{'} (x) \cdot d x

of an arbitrary differentiable function g.

Now, if we substitute $t = g (x)$ , and consequently $d t = g^{'} (x) d x$ we simply get the identity

\int_{a}^{b} f (g (x)) \cdot g^{'} (x) d x = \int_{g (a)}^{g (b)} f (t) d t

and it is is a valid one, guaranteed by the substitution formula! For the readers convenience the examples to follow are displayable either way. Just click the buttons ◄ and ► to choose your option.

The substitution formula is bidirectional. We use the left to right direction if the integrand is clearly shaped like $(f \circ g) \cdot g^{'}$ . In this case the substituition g is simply read off.

With the second direction (right to left) we have to introduce independently a substitution g such that the integral of $(f \circ g) \cdot g^{'}$ is easier to calculate than the one of f. Further we now need to find inverse images of the boundaries with respect to g. If g is bijective we can employ the inverse function of g and restate [8.3.5] for $a, b \in I$ as follows:

$\int_{a}^{b} f = \int_{g^{- 1} (a)}^{g^{- 1} (b)} (f \circ g) \cdot g^{'}$

We start practising with two examples for the left to right direction.

Example: We calculate the integral $\int_{0}^{1} (X^{2} + 1)^{4} \cdot 2 X = \int_{0}^{1} (x^{2} + 1)^{4} \cdot 2 x d x$ by substituting

◄►

$g = X^{2} + 1, g^{'} = 2 X$

\begin{array}{l} \int_{0}^{1} (X^{2} + 1)^{4} \cdot 2 X \\ = & \int_{0}^{1} X^{4} \circ (X^{2} + 1) \cdot (X^{2} + 1)^{'} \\ = & \int_{1}^{2} X^{4} \\ = & \frac{1}{5} X^{5} |_{1}^{2} = \frac{31}{5} \end{array}

$t = x^{2} + 1, d t = 2 x d x$

\begin{array}{l} \int_{0}^{1} (x^{2} + 1)^{4} \cdot 2 x d x \\ = & \int_{1}^{2} t^{4} d t \\ = & \frac{1}{5} t^{5} |_{1}^{2} = \frac{31}{5} \end{array}

The first step in the next example is to care for the missing factor 3. This is easily done by considering $1 = \frac{1}{3} \cdot 3$ , a common trick. Unsuitable factors are no obstacles at all as they are always placeable outside the integral sign.

Example: To calculate the integral $\int_{0}^{2} \frac{X^{2}}{2 \sqrt{X^{3} + 1}} = \int_{0}^{2} \frac{x^{2}}{2 \sqrt{x^{3} + 1}} d x$ we substitute

◄►

$g = X^{3} + 1, g^{'} = 3 X^{2}$

\begin{array}{l} \int_{0}^{2} \frac{X^{2}}{2 \sqrt{X^{3} + 1}} \\ = & \frac{1}{3} \int_{0}^{2} \frac{3 X^{2}}{2 \sqrt{X^{3} + 1}} \\ = & \frac{1}{3} \int_{0}^{2} \frac{1}{2 \sqrt{X}} \circ (X^{3} + 1) \cdot (X^{3} + 1)^{'} \\ = & \frac{1}{3} \int_{1}^{9} \frac{1}{2 \sqrt{X}} \\ = & \frac{1}{3} \sqrt{X} |_{1}^{9} = \frac{2}{3} \end{array}

$t = x^{3} + 1, d t = 3 x^{2} d x$

\begin{array}{l} \int_{0}^{2} \frac{x^{2}}{2 \sqrt{x^{3} + 1}} d x \\ = & \frac{1}{3} \int_{0}^{2} \frac{1}{2 \sqrt{x^{3} + 1}} \cdot 3 x^{2} d x \\ = & \frac{1}{3} \int_{1}^{9} \frac{1}{2 \sqrt{t}} d t \\ = & \frac{1}{3} \sqrt{t} |_{1}^{9} = \frac{2}{3} \end{array}

In our third example we apply the substitution formula in the right to left direction. Now that the integrand is not of the $(f \circ g) \cdot g^{'}$ type there is no evident substitution g to be read off. Without experiences some substitutions seem to be quite random and strange.

In this example we choose sine for substitution as the integrand's design is related to the Pythagorean theorem $1 - \sin^{2} = \cos^{2}$ which might be promising. Also, in a previous example we already proved $\frac{1}{2} (\sin \cdot \cos + X)$ to be a primitive of $\cos^{2}$ .

Example: We solve the integral $\int_{- 1}^{1} \sqrt{1 - X^{2}} = \int_{- 1}^{1} \sqrt{1 - x^{2}} d x$ by substituting

◄►

$g = \sin, g^{'} = \cos$

\begin{array}{l} \int_{- 1}^{1} \sqrt{1 - X^{2}} \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - X^{2}} \circ \sin \cdot \sin^{'} \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - \sin^{2}} \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{\cos^{2}} \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} | \cos | \cdot \cos \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} = \frac{1}{2} (\sin \cdot \cos + X) |_{- \frac{π}{2}}^{\frac{π}{2}} = \frac{π}{2} \end{array}

$x = \sin t, d x = \cos t d t$

\begin{array}{l} \int_{- 1}^{1} \sqrt{1 - x^{2}} d x \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{1 - \sin^{2} t} \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \sqrt{\cos^{2} t} \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} | \cos t | \cdot \cos t d t \\ = & \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} t d t \\ = & \frac{1}{2} (\sin t \cdot \cos t + t) |_{- \frac{π}{2}}^{\frac{π}{2}} = \frac{π}{2} \end{array}

In a final example we use both directions of the substitution formula to calculate a primitive function of

\sqrt{1 - \frac{X^{2}}{r^{2}}} : [- r, r] \to ℝ

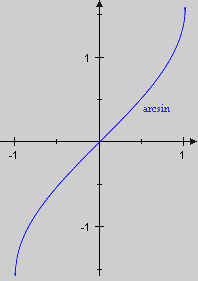
for an arbitrary $r > 0$ . Again we take sine for substitution as the new function is quite similar to the last one. This time however the boundaries are variable so that g needs to be reversible. sine itself is not bijective but the restriction $\sin | [- \frac{π}{2}, \frac{π}{2}]$ is. Its invers function

\arcsin = {(\sin | [- \frac{π}{2}, \frac{π}{2}])}^{- 1} : [- 1, 1] \to [- \frac{π}{2}, \frac{π}{2}]

is called inverse sine. We only use the dx-notation for this example.

Example: We recall that $\frac{1}{2} (\sin \cdot \cos + X)$ is a primitive of $\cos^{2}$ . As cosine is positive on the range $\arcsin ([- 1, 1]) = [- \frac{π}{2}, \frac{π}{2}]$ we calculate for an arbitrary $x \in [- r, r]$ (using Pythagoras' theorem again)

\begin{array}{l} \int_{- r}^{x} \sqrt{1 - \frac{u^{2}}{r^{2}}} d u & = r \int_{- r}^{x} \sqrt{1 - \frac{u^{2}}{r^{2}}} \cdot \frac{1}{r} d u \\ = r \int_{- 1}^{\frac{x}{r}} \sqrt{1 - t^{2}} d t substitute t = \frac{u}{r}, d t = \frac{1}{r} d u \\ = r \int_{\arcsin (- 1)}^{\arcsin \frac{x}{r}} \sqrt{1 - \sin^{2} z} \cdot \cos z d z substitute t = \sin z, d t = \cos z d z \\ = r \int_{\arcsin (- 1)}^{\arcsin \frac{x}{r}} \cos^{2} z d z \\ = \frac{r}{2} (\sin z \cdot \cos z + z) |_{- \frac{π}{2}}^{\arcsin \frac{x}{r}} \\ = \frac{r}{2} (\frac{x}{r} \cdot \cos (\arcsin \frac{x}{r}) + \arcsin \frac{x}{r} + \frac{π}{2}) \end{array}

and thus have established a primitive function of $\sqrt{1 - \frac{X^{2}}{r^{2}}}$ , namely:

\frac{X}{2} \cdot \cos (\arcsin \frac{X}{r}) + \frac{r}{2} \cdot \arcsin \frac{X}{r} = \frac{X}{2} \cdot \sqrt{1 - \frac{X^{2}}{r^{2}}} + \frac{r}{2} \cdot \arcsin \frac{X}{r}

We close this part by proving that integrals are translation-resistant which is easily done with the substitution formula..

Proposition: Let f be integrable on I and $a, b \in I$ . For each $c \in ℝ$ we have:

\int_{a}^{b} f = \int_{a + c}^{b + c} f \circ (X - c)

[8.3.6]

Proof: As $(X - c)^{'} = 1$ we may employ the substitution formula and get

\int_{a + c}^{b + c} f \circ (X - c) = \int_{X - c (a + c)}^{X - c (b + c)} f = \int_{a}^{b} f

8.2. 8.4.