8.5. Calculating Content
We are now going to develop a general concept for calculating content. We will do this by assigning adequate values to suitable subsets M of that, in the two-dimensional case coincide with the areas introduced in 8.4 and meet our image of a volume in the three-dimensional one.
These values will be recursively designed, as suggested by the interpretation of areas at the end of 8.4: The (n + 1)-dimensional content of a set M will result from integrating the n-dimensional contents of its sections .
|
Definition: For a subset of and any the set
|
[8.5.1] |
is called a section in M.
|
The following applet visualises a section in a sugar loaf at (display by
JavaView
i  |
|
JavaView is an interactive 3D geometry viewer. Display is controlled by the left-mouse, for example:
-
press "o" and drag to rotate (preset)
-
press "s" and drag to scale
-
press "t" and drag to translate
Go to www.javaview.de/jars/shortcuts.html for a complete list of options. The right-mouse launches an extensive context menu.
|
).
As a start we calculate sections in some manageable subsets of and of . All the parameters in this and the subsequent examples are strictly positive.
|
Example:
-
All sections in a Square are (constant) intervals as we have for any :
|
[1] |
-
The sections in an ellipse are (variable) intervals as we calculate for each :
|
[2] |
Note that when the interval is a singleton: .
-
Sections in a perforated disc are a bit laborious to calculate. Let us just start with an :
|
[3] |
If the sections in L are one- or two-element sets:
-
Sections in a cube are (constant) squares because we have for :
|
[4] |
-
Sections in a sphere
are circles (with varying radii) as we have for every :
|
[5] |
If the section is a circle with radius 0, i.e. a point.
|
Now we define by recursion which sets are suitable for measuring content and how to calculate it. The remarks at the end of the previous section serve as a guideline.
|
Definition:
-
A subset has a one-dimensional content if is a disjoint union

i  |
|
The union of two sets A and B is called disjoint if . In that case the symbol is often replaced by .
Display problems should be solved by downloading the font Lucida Bright Math Symbol.
|
of finitely many closed intervals, . In that case we call the number
|
[8.5.2] |
the one-dimensional content of M. In addition we set: .
-
A subset , , has an ()-dimensional content if every section , , has an n-dimensional content such that the funtion is integrable on . In this case the number
|
[8.5.3] |
is called the ()-dimensional content of M. If we additionally set: .
|
Consider:
-
Sometimes, especially in three-dimensional situations, the term volume is used instead of content.
-
A simple inductive argument shows that contents are positive: .
-
Due to the different add ons the content of any finite set is zero:
-
[8.5.2] includes the common special case . M then is a simple interval, , , and the content shortens to .
-
[8.5.3] infact introduces the Cavalieri Principle:
If any two sets have a content such that all of their sections have the same content then they coincide in their own content as well:
|
[8.5.4] |
-
[8.5.2] carries forward the area concept of 8.4 as the areas calculated there now reappear as two-dimensional contents: For any positive function the set
has a two-dimensional content that is exactly the area of the region generated by f and the x-axis on .
Proof: For we have: , so that . Therefor the content of M is calculated to
In a first example we recalculate the content of some well known two-dimensional objects.
Example: |
Square |
Ellipse |
Circle |
Perforated Disc |
Line |
Rectangle |
Triangle |
|
-
The content of a square with edge length a is
|
[6] |
Proof: According to [1] all sections in Q have a constant content:
Thus is integrable on so that Q has a content, namely
-
The content of an ellipse with semi axes a and b is
|
[7] |
Proof: From [2] we know that the sections in E are the intervals
As the continuous function is integrable on , E has a content that we calculate by using an integral from 8.4:
-
The content of a circle (disc) with radius r is
|
[8] |
Proof: D is an ellipse with identical semi axes . Thus: .
-
The content of a perforated disc with radii is
|
[9] |
Proof: Due to [3] the sections in a perforated disc are calculated like this:
Thus their content (even in the special case ) is given by
is representable as the concatenation of the restrictions , and and thus integrable according to [8.1.14], so that the content of L could be calculated (use an integral from 8.4) to
-
For any function the content of the line f is
|
[10] |
Proof: As all the sections are singletons of content 0. Therefor we have
-
The content of a rectangle with edge lengths a and b is
|
[11] |
Proof:
?
We have: with sections of constant content: . Thus R has a content, namely
-
The content of a triangle with base and height h is
|
[12] |
Proof:
?
The sections in are (variable) intervals and the function is integrable. Thus D has the content
|
In the next example we calculate some of the classical three-dimensional volumia using our previous results [6] to [9].
Example: |
Cube |
Ellipsoid |
Sphere |
Cone |
Pyramid |
Torus |
Cuboid |
Cylinder |
|
-
The content of a cube of edge length a is
Proof: Due to [6] the sections (see [4]) in have the constant content . Thus W has a content, namely
-
The content of an ellipsoid with semi axes a, b and c is
Proof: At first we see that . If the inequality
only holds for . If it is equivalent to
Thus is either a point or an ellipse (see [7]) with semi axes and . In either case the content of equals to
and as is integrable E has a content:
-
The content of a sphere of radius r is
Proof: S is an ellipsoid with three identical semi axes: . The content of a sphere is thus a special case of the content for an ellipsoid.
For a separate proof without using the ellipsoid formula we consider the sections according to [5]:
.
is a circle with radius (or a point if resp.). Due to [8] its content calculates to . As the continuous function is integrable on , S has a content, namely:
-
The content of a cone of height h and radius r is
Proof: We notice that and for any we get
.
Thus is a circle again (a point if ). Due to [8] we find the function which is integrable on and from that we eventually get the content
-
The content of a pyramid with height h and rectangular base is
Proof: and
for each . Thus is a point if and a rectangle with edge length and otherwise. The integrable function now yields the content:
-
We abbreviate and and consider the set
T is a torus with radii r and R.

i  |
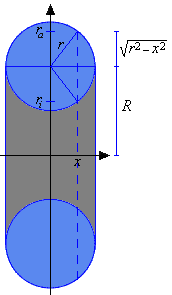 The sketch to the left shows a torus with radii r and R vertically halfed with respect to the z-axis. It explaines how the inner () and the outer () radius of a section is calculated.
|
Its content is
Proof: We see that and that the section
is a perforated disc for each . According to [9] the content of is given by
is integrable, thus T has a content, namely (the integral involved has been evaluated in 8.4)
-
The content of a cuboid of edge length a, b and c is
Proof:
?
We have and for all . thus is a rectangle with edge length b and c. As the constant function is integrable on the cuboid Q has the content
-
The content of a cylinder
of height h and radius r is
Proof:
?
We note that . For each the section is a circle of a fixed radius r, which means is a constant and thus integrable function, so that Z has a content, namely
|
Some of the examples above (for instance the sphere and the cone) represent a general class of subsets of that have a content, the so-called solids of revolution. They are turn-shaped and are generated by a function rotating around the x-axis.
|
Notation and Proposition: For any continuous function the set
|
[8.5.5] |
is called the solid of revolution generated (on ) by the casing function f. R has the content
Proof: We note that and that is a circle of radius for each . So we have: , which is infact the assertion.
|
As an example we calculate the content of the solid of revolution R (pulley) generated on by the casing function :
|
Exercise: The content of the ellipsoid

i  |
|
The ellipsoid in this exercise is characterised by two identical semi axes, namely b which is the semi axis in y and z direction as well. This is due to the fact that E is generated as rotational solid by the upper semi ellipse .
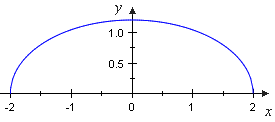
semi ellipse with a = 2 and b = 1.2
For the radius that is required to calculate the sections we look at the following consideration:
|
calculates to .
Proof:
?
We see from the annotation that E is the solid of revolution
generated on by . Its content is thus given by
|
If we turn to n-dimensional content, employment of the induction principle is unavoidable. As a first example we calculate the content of an n-dimensional cube and an n-dimensional sphere respectively.
|
Proposition:
-
The content of the n-dimensional cube is
|
[8.5.6] |
-
The content of the n-dimensional sphere is
|
[8.5.7] |
1. ► Proof by induction:
-
: is a closed interval such that .
-
: Now let be an -dimensional cube. For any we see that the section is an n-dimensional cube, thus having a content due to the induction hypothesis. The constant function is integrable, so that has a content as well, namely
2. ► Proof by induction:
-
: is a closed interval such that
Note that in this case.
-
: Next let be an ()-dimensional sphere. The section is an n-dimensional sphere for all , thus has a content according to the induction hypothesis. The function
is continuous, and that means integrable as well, so that has a content.
The integral (substituting , see [8.3.5])
now allows to calculate the ()-dimensionale sphere's content:
|
We follow up our subject and consider now generalised cones and cylinders. For an arbitrary non-empty subset
of we call the set
-
|
[8.5.8] |
a (generalised) cylinder with base G and height h.
-
|
[8.5.9] |
a (generalised) cone with base G and height h.
Consider:
-
Only if the base is an area in the usual sense, of course.
-
A (generalised) pyramide is a cone whose base is a polytope.
|
Exercise: If G has a content then the cylinder has a content as well. It calculates to
|
[8.5.10] |
As an example the cylinder , whose base is a sphere of radius 3 has the content .
Proof:
?
It is not necessary to prove by induction in this case as we have for all , so that is constant and thus
|
Obviously [8.5.10] confirms the well-known formula "base times hight" for the content of a cylinder. In order to get a similar result for a cone we need some technical preparations: For any two vectors and , , and an arbitrary subset we set
If or we write and respectively. is generated from M by dilation with the dilation vector c whereas is generated by translation with the translation vector d.
The following proposition will not only provide the desired formula for cones but will yield further important results as well.
|
Proposition: A subset has a content if and only if has a content. In this case we have:
|
[8.5.11] |
Proof: It is sufficient to prove only the "" direction because it includes the reverse direction already due to the identity
We proceed now by induction.
-
: If then as well and both sets have the same content 0.
For we have
which is again a disjoint union of closed intervals, having thus a content, namely:
-
: Now consider , i.e. . If then and the content of either set is 0. Assume now . At first we have
[+]
for all , because:
Now, if M has a content so does every section and is integrable on . Due to the induction hypothesis
has the content for each . According to the substitution formula [8.3.5] the function integrable and the content of is calculated like this:
|
There are some interesting implications of [8.5.11]:
-
Content is translation-proof, as for we have
|
[8.5.12] |
-
Content is dilation-compatible, as for we have
|
[8.5.13] |
-
Content is shearing-proof: If has a content then for any shear vector the set
has a content of the same size:
|
[8.5.14] |
Proof: For we see that . According to [8.5.12] thus has the content , so that the Cavalieri Principle [8.5.4] yields the assertion.
Now that content is compatible with dilation we are able to compute the content of a cone.
|
Proposition: The cone
has a content if its base has a content. In this case it calculates to:
|
[8.5.15] |
Proof: For any we have . Along with G the section has a content as well (see [8.5.13]), namely . Being a multiple of the function is integrable, i.e. C has the content
|
Consider:
-
The content formula [8.5.15] of course comprises the previously calculated formulas for triangles, three-dimensional circular cones and pyramids.
-
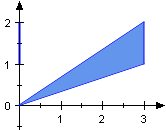
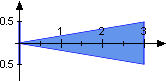
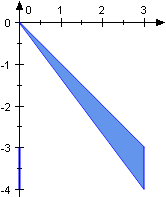
The height of a cone might be perpendicular to the base, but does not need to. Its position has no impact on the content due to [8.5.14]. All three triangles below for instance have the same content of 1.5.
|