8.9. Generalised Exponential and Logarithm Functions

e^{X}

is the invers of ln we see that, according to the laws of logarithms,

a^{n} = e^{\ln (a^{n})} = e^{n \cdot \ln a}

for all $a > 0$ and $n \in ℤ$ . This is an alternative way to calculate powers, a way however that we may well use as a guideline to introduce powers with arbitrary real exponents.

Definition: Let $a, x \in ℝ$ be arbitrary with $a > 0$ . We set

a^{x} ≔ e^{x \cdot \ln a}

[8.9.1]

As before we call a the base and x the exponent of the power $a^{x}$ . Being a value of the exponential function each power is strictly positive: $a^{x} > 0$ .

Note that, due to [8.8.25], we are allowed to use the notation $a^{x} = \exp (n \cdot \ln a)$ as well.

The new concept of powers is only applicable with a positive base. In this case, however we want to know if the new concept is a sequel to the common one. Thus we have to answer two questions:

Do new and old values coincide for all $x \in ℚ$ ?
Are the laws of exponents still valid?

We have a positive answer to both of them.

Proposition: If $a > 0$ we have for each $x \in ℚ$ :

a^{x} = \exp (x \cdot \ln a)

[8.9.2]

Proof: Say $x = \frac{n}{m}$ , $m > 0$ . Due to [8.8.2] and [8.7.6;10] we then have for $a^{x}$ in its old meaning:

a^{x} = a^{\frac{n}{m}} = \sqrt[m]{a^{n}} = \exp (\ln \sqrt[m]{a^{n}}) = \exp (\frac{n}{m} \cdot \ln a) = \exp (x \cdot \ln a)

We now turn to the laws of exponents. Besides the properties [8.8.2;3] we need the laws of logarithms [8.7.8;9] and the calculation rules for $e^{X}$ [8.8.15;16].

Proposition (laws of exponents): If $a, b > 0$ the following properties hold for every $x, y \in ℝ$ :

1. $a^{x} \cdot b^{x} = {(a \cdot b)}^{x}$	$\frac{a^{x}}{b^{x}} = (\frac{a}{b})^{x}$	$\frac{1}{b^{x}} = (\frac{1}{b})^{x}$	[8.9.3]
2. $a^{x} \cdot a^{y} = a^{x + y}$	$\frac{a^{x}}{a^{y}} = a^{x - y}$	$\frac{1}{a^{y}} = a^{- y}$	[8.9.4]
3. $\ln (a^{x}) = x \cdot \ln a$	${(\exp a)}^{x} = \exp (x \cdot a)$		[8.9.5]
4. $(a^{x})^{y} = a^{x \cdot y}$			[8.9.6]

Proof:

1. ► $a^{x} \cdot b^{x} = e^{x \cdot \ln a} \cdot e^{x \cdot \ln b} = e^{x \cdot \ln a + x \cdot \ln b} = e^{x \cdot (\ln a + \ln b)} = e^{x \cdot \ln (a \cdot b)} = {(a \cdot b)}^{x}$

$\frac{a^{x}}{b^{x}} = \frac{e^{x \cdot \ln a}}{e^{x \cdot \ln b}} = e^{x \cdot \ln a - x \cdot \ln b} = e^{x \cdot (\ln a - \ln b)} = e^{x \cdot \ln \frac{a}{b}} = {(\frac{a}{b})}^{x}$

The third equation is a special case of the second one.

2. ► $a^{x} \cdot a^{y} = e^{x \cdot \ln a} \cdot e^{y \cdot \ln a} = e^{x \cdot \ln a + y \cdot \ln a} = e^{(x + y) \cdot \ln a} = a^{x + y}$

$\frac{a^{x}}{a^{y}} = \frac{e^{x \cdot \ln a}}{e^{y \cdot \ln a}} = e^{x \cdot \ln a - y \cdot \ln a} = e^{(x - y) \cdot \ln a} = a^{x - y}$

Again, the third equation follows from the one before.

3. ► $\ln (a^{x}) = \ln (e^{x \cdot \ln a}) = x \cdot \ln a$

${(\exp a)}^{x} = e^{x \cdot \ln (\exp a)} = e^{x \cdot a}$

4. ► $(a^{x})^{y} = e^{y \cdot \ln (a^{x})} \underset{3 .}{=} e^{y \cdot x \cdot \ln a} = a^{x \cdot y}$

In a first application of the new power concept we study exopnential equations, i.e. equations of the type

a^{x} = b

If $a \neq 1$ we get their unique solution by taking the logarithm on both sides.

Proposition and Definition: For $a, b > 0$ , $a \neq 1$ the following equivalence holds

a^{x} = b \Leftrightarrow x = \frac{\ln b}{\ln a}

[8.9.7]

The number $\log_{a} b ≔ \frac{\ln b}{\ln a}$ is called the logarithm to the base a of b. Apparently $\log_{a} b$ is that certain number that yields b if we take a to its power:

a^{\log_{a} b} = b

Proof: We use [8.9.5] to get: $a^{x} = b \Leftrightarrow \ln a^{x} = \ln b \Leftrightarrow x \cdot \ln a = \ln b \Leftrightarrow x = \frac{\ln b}{\ln a}$ .

The logarithms to a fixed base a allow to introduce generalised logarithm functions.

Definition: For any $a > 0$ , $a \neq 1$ we call the function

\log_{a} : ℝ^{> 0} \to ℝ

[8.9.8]

the (generalised) logarithm function to the base a. Instead of $\log_{a} (x)$ we often write $\log_{a} x$ which is more common. Also, we note that every logarithm function is just a multiple of ln: $\log_{a} = \frac{1}{\ln a} \cdot \ln$ .

With $\ln e = 1$ we have $\log_{e} = \ln$ , thus the logarithm to the base e is the natural logarithm. Two further logarithm functions have names for their own:

the common logarithm $\lg ≔ \log_{10}$
the binary (or dual) logarithm $ld ≔ \log_{2}$

As the logarithms are multiples of ln they take over most of its properties. The laws of logarithms [8.7.6-10] for example analogously hold for $\log_{a}$ as well. Furthermore, $\log_{a}$ is integrable and arbitrary often differentiable. Its graph is the result of a perpendicular dilation of that of ln:

Now that the concept of power has been extended new functions could be introduced. Generalised power functions are our first example.

Definition: For any real a the function

X^{a} ≔ e^{a \cdot \ln} : ℝ^{> 0} \to ℝ

[8.9.9]

is called the (generalised) power function with exponent a. Obviously $X^{a} (x) = e^{a \cdot \ln x} = x^{a}$ .

Power functions are differentiable and integrable. Derivatives and primitives follow the "common scheme":

Proposition: Each power function $X^{a}$ is

1. differentiable with $(X^{a})^{'} = a X^{a - 1}$	[8.9.10]
2. arbitrary differentiable and $(X^{a})^{(n)} = \prod_{i = 0}^{n - 1} (a - i) \cdot X^{a - n}$ for all $n > 0$	[8.9.11]
3. integrable and $\frac{1}{a + 1} X^{a + 1}$ is a primitive of $X^{a}$ if $a \neq - 1$ .	[8.9.12]

Proof:

1. ► Differentiability is due to the chain rule [7.7.8] which also provides the derivative:

(X^{a})^{'} = (e^{X} \circ a \cdot \ln)^{'} = ((e^{X})^{'} \circ a \cdot \ln) \cdot a \cdot \ln^{'} = (e^{X} \circ a \cdot \ln) \cdot a \cdot X^{- 1} = X^{a} \cdot a \cdot X^{- 1} = a X^{a - 1}

2. ► The proof is by induction with the base step already done in 1. Thus assume $X^{a}$ is n-times differentiable and the derivative formula [8.9.11] is valid. Note that the nth derivative $(X^{a})^{(n)} = \prod_{i = 0}^{n - 1} (a - i) \cdot X^{a - n}$ is a multiple of a power function and thus differentiable as well with

{(X^{a})}^{(n + 1)} = \prod_{i = 0}^{n - 1} (a - i) \cdot (X^{a - n})^{'} = \prod_{i = 0}^{n - 1} (a - i) \cdot (a - n) \cdot X^{a - n - 1} = \prod_{i = 0}^{n} (a - i) \cdot X^{a - (n + 1)}

3. ► The case $a = - 1$ is well-known. If $a \neq - 1$ we may differentiate the function $\frac{1}{a + 1} X^{a + 1}$ according to 1. and get $X^{a}$ as its derivative.

The generalised exponential functions are another application of the extended power concept.

Definition: For each $a > 0$ the function

a^{X} ≔ e^{X \cdot \ln a} : ℝ \to ℝ^{> 0}

[8.9.13]

is called the (generalised) exponential function with base a. Its values are $a^{X} (x) = e^{x \cdot \ln a} = a^{x}$ .

Two of the exponential functions are not new for us:

The exponential function with base 1 is the constant function 1, actually because $\ln 1 = 0$ :

$1^{X} = e^{X \cdot \ln 1} = e^{0} = 1$
The exponential function with base e is the natural exponential function $e^{X} = \exp$ . This is due to $\ln e = 1$ :

$e^{X} = \exp \circ (X \cdot \ln e) = \exp \circ X = \exp$

This identity now justifies the power notation for the exponential function in terms of content: The natural exponential function is a special exponential function, namely that with base e. Thus the notation introduced in 8.8 is more than a symbolic one.

As the values of exponential functions are powers the laws of exponents [8.9.4-6] apply and thus provide respective rules for these functions. As an example we we note

a^{X} (x + 1) = a^{X} (x) \cdot a^{X} (1) = a \cdot a^{X} (x)

as a special case of [8.9.4], which means: If we increment x by one unit the value turns to the a-fold one.

The inner function of the decomposition $a^{X} = e^{X} \circ X \cdot \ln a$ is a multiple of X. The graph of an exponential function thus is the result of a horizontal dilation of that of $e^{X}$ :

Exponential functions are differentiable and integrable. Calculating their derivatives and primitives is an easy task.

Proposition: Every exponential function $a^{X}$ is

1. differentiable with $(a^{X})^{'} = \ln a \cdot a^{X}$	[8.9.14]
2. arbitrary often differentiable and $(a^{X})^{(n)} = {(\ln a)}^{n} \cdot a^{X}$ for all $n > 0$	[8.9.15]
2. integrable and $\frac{1}{\ln a} a^{X}$ is a primitive of $a^{X}$ if $a \neq 1$	[8.9.16]

Proof:

1. ► Again, differentiability and derivative formula are due to the chain rule [7.7.8]:

(a^{X})^{'} = (e^{X} \circ X \cdot \ln a)^{'} = ((e^{X})^{'} \circ X \cdot \ln a) \cdot (X \cdot \ln a)^{'} = (e^{X} \circ X \cdot \ln a) \cdot \ln a = \ln a \cdot a^{X}

2. ► This is a straightforward proof by induction with the base step already shown by 1. For the induction step we just note that the nth derivative of $a^{X}$ is a multiple of $a^{X}$ and therefor differentiable. Its derivative $(a^{X})^{(n)}$ just adds the factor $\ln a$ another time so that the derivative formula is valid for $(a^{X})^{(n + 1)}$ as well.

3. ► The case $1^{X} = 1$ is trivial and if $a \neq 1$ we just need to differentiate the function $\frac{1}{\ln a} a^{X}$ which is easily done using 1.

$e^{X}$ and ln are inverse functions to each other. This is also true for generalised exponential and logarithm functions.

Proposition: If $a > 0$ , $a \neq 1$ then $a^{X}$ and $\log_{a}$ are invers to each other:

\begin{array}{l} a^{X} \circ \log_{a} = X | ℝ^{> 0} \\ \log_{a} \circ a^{X} = X \end{array}

[8.9.17]

Proof: We only need to show that both functions cancel out each other:

The identity $a^{\log_{a} x} = x$ is valid for all $x > 0$ according to [8.9.7].
$\log_{a} (a^{x}) = \frac{1}{\ln a} \cdot \ln (a^{x}) = \frac{1}{\ln a} \cdot x \cdot \ln a = x$ holds for all x due to [8.9.8] and [8.9.5].

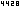8.8.