8.8. The Exponential Function

In the previous part we proved the logarithm

\ln : ℝ^{> 0} \to ℝ

to be invertible. Now we concentrate on its inverse function

\ln^{- 1}

which will be denoted by a symbol of its own: The function

e^{X} ≔ \ln^{- 1} : ℝ \to ℝ^{> 0}

[8.8.1]

is called the (natural) exponential function.

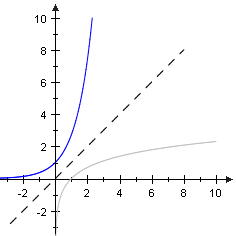The unexpected choice of a power symbol for the exponential function will be justified in 8.9. Furthermore we will prove the identity $e^{X} = \exp$ in [8.8.25], so that the name "exponential function" won't cause any conflict with respect to [5.9.18]. [8.8.1] thus provides an alternative access to the exponential function that does not depend on series. Many of its properties follow directly from the respective ones of the logarithm. The graph for example is instantly available as the reflection of ln in the line $y = x$ .

To begin with we state the charcteristic properties of an inverse function for $e^{X}$ .

Proposition:

1. $e^{\ln x} = x$ for all $x > 0$ .	[8.8.2]
2. $\ln e^{x} = x$ for all $x \in ℝ$ .	[8.8.3]

Proof: A function and its inverse cancel out each other's effect:

\begin{array}{l} e^{X} \circ \ln = X | ℝ^{> 0} \\ \ln \circ e^{X} = X \end{array}

but this is exactly what 1. and 2. are saying.

[8.8.2] allows to compute our first two values of the exponential function:
As $\ln 1 = 0$ and $\ln e = 1$ (see [8.7.12]) we get:

\begin{array}{l} e^{0} = e^{\ln 1} = 1 \\ e^{1} = e^{\ln e} = e \end{array}

[8.8.4]

With the logarithm's main inequality we will be able to evaluate $e^{X}$ at each point. To that end however, we first need to know something about the analytical properties of the exponential function.

Proposition:

1. $e^{X}$ is continuous.	[8.8.5]
2. $e^{X}$ is differentiable and $(e^{X})^{'} = e^{X}$ .	[8.8.6]
3. $e^{X}$ is arbitrary often differentiable and $(e^{X})^{(n)} = e^{X}$ .	[8.8.7]
4. $e^{X}$ is integrable and $e^{X}$ is one of its primitives.	[8.8.8]

Proof: Firstly we note that $\ln^{'} (x) = \frac{1}{x} \neq 0$ for all $x > 0$ .

1. ► The continuity of $e^{X} = \ln^{- 1}$ at each $x \in ℝ$ is thus guaranteed by [7.5.3].

2. ► The differentiability of $e^{X}$ at x follows from [7.5.4] as well as

(e^{X})^{'} (x) = (e^{X})^{'} (\ln e^{x}) = \frac{1}{\ln^{'} (e^{x})} = \frac{1}{\frac{1}{e^{x}}} = e^{x}

for all

x \in ℝ

3./4. ► Both assertions are an immediate consequence of 2.

The outstanding importance of the exponential function is laid out by [8.8.6]: It is a non-trivial function that coincides with its own derivative, i.e. a function $f \neq 0$ satisfying the "differential equation" $f^{'} = f$ .

Now that continuity is placed at our disposal we are able to calculate the values of $e^{X}$ as promised before.

Proposition: For all $x \in ℝ$ we have:

e^{x} = \lim (1 + \frac{x}{n})^{n}

[8.8.9]

Proof: Take a fixed $x \in ℝ$ and an arbitrary $n > - x$ . Then $\frac{x}{n} > - 1$ , i.e. $1 + \frac{x}{n} > 0$ . The main inequlity[8.7.11] thus allows to estimate $\ln (1 + \frac{x}{n})^{n} = n \cdot \ln (1 + \frac{x}{n})$ as follows:

\underset{\to x}{\underset{︸}{\frac{n x}{n + x}}} = n (1 - \frac{1}{1 + \frac{x}{n}}) \leq \ln (1 + \frac{x}{n})^{n} \leq n (1 + \frac{x}{n} - 1) = \underset{\to x}{\underset{︸}{x}}

According to the nesting theorem [5.5.8] we see that $\lim \ln (1 + \frac{x}{n})^{n} = x$ . Using [8.8.2] and the continuity of the exponential function we now get

e^{x} = e^{\lim \ln (1 + \frac{x}{n})^{n}} = \lim e^{\ln (1 + \frac{x}{n})^{n}} = \lim (1 + \frac{x}{n})^{n}

We now turn to some elementary properties of $e^{X}$ . From 1. and 2. in the subsequent proposition we learn that the exponential function has no zeros, no extreme values and no inflection points.

Proposition:

1. $e^{x} > 0$ for all $x \in ℝ$ .	[8.8.10]
2. $e^{X}$ is strictly increasing and strictly convex (curved to the left).	[8.8.11]
3. $e^{x} < 1$ for all $x < 0$ .	[8.8.12]
4. $e^{x} > 1$ for all $x > 0$ .	[8.8.13]

Proof:

1. ► just restates the fact that $ℝ^{> 0}$ is the exponential function's range: $e^{X} : ℝ \to ℝ^{> 0}$ .

2. ► Due to 1. we have $(e^{X})^{'} (x) = (e^{X} {)^{'}}^{'} (x) > 0$ for all x. The assertion thus follows from the strict versions of the monotony and convexity test respectively ([7.10.5] and [7.10.13]).

3./4. ► follows immediately from the strict monotony if we consider the value $e^{0} = 1$ .

Many properties of the exponential function are a direct mirror of the respective properties of the logarithm. A good example for that are the following calculation rules.

Proposition (calculation rules for $e^{X}$ ): For all $a, b \in ℝ$ , $n \in ℤ$ the following identities hold:

1. $e^{- b} = \frac{1}{e^{b}}$	[8.8.14]
2. $e^{a + b} = e^{a} \cdot e^{b}$	[8.8.15]
3. $e^{a - b} = \frac{e^{a}}{e^{b}}$	[8.8.16]
4. $e^{n \cdot a} = (e^{a})^{n}$	[8.8.17]
5. $e^{\frac{1}{n} \cdot a} = \sqrt[n]{e^{a}}$ for $n > 0$	[8.8.18]

Proof: Each proof uses the identities $x = \ln e^{x}$ and $x = e^{\ln x}$ (see [8.8.2/3]).

1. ► follows from [8.7.7]: $e^{- b} = e^{- \ln e^{b}} = e^{\ln \frac{1}{e^{b}}} = \frac{1}{e^{b}}$ ,

2. ► from [8.7.8]: $e^{a + b} = e^{\ln e^{a} + \ln e^{b}} = e^{\ln (e^{a} \cdot e^{b})} = e^{a} \cdot e^{b}$ ,

3. ► from [8.7.9]: $e^{a - b} = e^{\ln e^{a} - \ln e^{b}} = e^{\ln \frac{e^{a}}{e^{b}}} = \frac{e^{a}}{e^{b}}$ ,

4. ► from [8.7.6]: $e^{n \cdot a} = e^{n \cdot \ln e^{a}} = e^{\ln (e^{a})^{n}} = (e^{a})^{n}$ and

5. ► from [8.7.10]: $e^{\frac{1}{n} \cdot a} = e^{\frac{1}{n} \cdot \ln e^{a}} = e^{\ln \sqrt[n]{e^{a}}} = \sqrt[n]{e^{a}}$ .

In another example for this 'shifting process' we transfer the main inequality [8.7.11] and its extension [8.7.13] and hence get the main inequality for the exponential function.

Proposition: For all $x \in ℝ$ the following estimates hold:

1. $x + 1 \leq e^{x} \leq x \cdot e^{x} + 1$	[8.8.19]
2. $(\frac{n + x}{n})^{n} \leq e^{x}$ if $n > - x$	[8.8.20]
3. $e^{x} \leq (\frac{n}{n - x})^{n}$ if $n > x$	[8.8.21]

Proof:

1. ► We evaluate the main inequality for ln at $e^{x}$ :

1 - \frac{1}{e^{x}} \underset{[1]}{\leq} \underset{= x}{\underset{︸}{\ln e^{x}}} \underset{[2]}{\leq} e^{x} - 1

The estimate $x + 1 \leq e^{x}$ follows immediately from [2], and multipliying [1] by $e^{x} > 0$ yields $e^{x} - 1 \leq x \cdot e^{x}$ , and thus: $e^{x} \leq x \cdot e^{x} + 1$ .

2./3. ► This time we evaluate the extension [8.7.13] at $e^{x}$ and get

n (1 - \frac{1}{\sqrt[n]{e^{x}}}) \underset{[3]}{\leq} x \underset{[4]}{\leq} n (\sqrt[n]{e^{x}} - 1)

[4] tells us that $\frac{n + x}{n} = 1 + \frac{x}{n} \leq \sqrt[n]{e^{x}}$ , and if $n > - x$ , i.e. $n + x > 0$ , this leads to

(\frac{n + x}{n})^{n} \leq e^{x}

[3] may be modified to $\frac{1}{\sqrt[n]{e^{x}}} \geq 1 - \frac{x}{n} = \frac{n - x}{n}$ , and if $n > x$ , i.e. $n - x > 0$ , we thus have

\frac{1}{e^{x}} \geq (\frac{n - x}{n})^{n} \Leftrightarrow e^{x} \leq (\frac{n}{n - x})^{n}

Now we study the exponential function's limit behaviour. Whereas [8.8.21] provides the limit if $x \to - \infty$ , [8.8.19] is responsible for its unboundedness, i.e. $\lim_{x \to \infty} e^{x} = \infty$ . Unboundedness comes in a very peculiar way of increasing controlled by [8.8.20]: $e^{X}$ approaches $\infty$ quicker than every positive power of X, which means that $x^{a} < e^{x}$ for sufficiently large x.

Proposition: For each $a \in ℝ^{> 0}$ ^*) we have:

1. $\lim_{x \to \infty} \frac{x^{a}}{e^{x}} = 0$	[8.8.22]
2. $\lim_{x \to - \infty} e^{x} = 0$	[8.8.23]

___________
*) Powers with arbitrary exponents are introduced in 8.9.

Proof:

1. ► Take a fixed $n > a$ . Due to [8.8.20] each $x > 0$ satisfies the estimate

0 \leq \frac{x^{a}}{e^{x}} \leq \frac{x^{a}}{(\frac{n + x}{n})^{n}} = n^{n} \cdot \frac{x^{a}}{{(n + x)}^{n}} \leq n^{n} \cdot \frac{x^{a}}{x^{n}} = n^{n} \cdot x^{a - n}

which in fact is the assertion as $\lim_{x \to \infty} x^{a - n} = 0$ .

2. ► We use [8.8.23] with $n = 1$ , which guarantees that

0 \leq e^{x} \leq \frac{1}{1 - x}

for all $x < 0$ . But as $\lim_{x \to - \infty} \frac{1}{1 - x} = 0$ , we also have $\lim_{x \to - \infty} e^{x} = 0$ .

In [5.9.18] we introduced the exponential function $\exp : ℝ \to ℝ$ by $\exp (x) = \sum_{i = 0}^{\infty} \frac{x^{i}}{i!}$ and promised to show that $e^{X} = \exp$ in [8.8.1]. We will now prove this identity using the Taylor series

\sum_{i = 0}^{\infty} \frac{f^{(i)} (a)}{i!} {(x - a)}^{i}

introduced in 7.9 (click for an alternative ad hoc proof). At first we calculate the Taylor polynomial and the Lagrange remainder of the $C^{\infty}$ -function $e^{X}$ . This is easily done due to the exponential function's pleasing derivative behaviour [8.8.7].

Proposition: Take $n \in ℕ$ . For each $x \neq 0$ there is an $\tilde{x}$ in between 0 and x such that

e^{x} = \sum_{i = 0}^{n} \frac{1}{i!} x^{i} + \frac{e^{\tilde{x}}}{(n + 1)!} x^{n + 1}

[8.8.24]

Proof: Using Taylor's theorem [7.9.16] with $a = 0$ and $(e^{X})^{(i)} = e^{X}$ yields:

e^{x} = \sum_{i = 0}^{n} \frac{e^{0}}{i!} x^{i} + \frac{e^{\tilde{x}}}{(n + 1)!} x^{n + 1} = \sum_{i = 0}^{n} \frac{1}{i!} x^{i} + \frac{e^{\tilde{x}}}{(n + 1)!} x^{n + 1}

for a suitable $\tilde{x}$ .

[8.8.24] is a major step and we now have the identity of both exponential functions at hand:

Proposition: For all $x \in ℝ$ we have

e^{x} = \sum_{i = 0}^{\infty} \frac{x^{i}}{i!}

[8.8.25]

Proof: There is nothing to show if $x = 0$ ( $e^{0} = 1 = \sum_{i = 0}^{\infty} \frac{1}{i!} 0^{i}$ ). So assume $x \neq 0$ . According to [8.8.24] we only need to show that the Lagrange remainder is a zero sequence:

\frac{e^{\tilde{x}}}{(n + 1)!} x^{n + 1} \to 0

$e^{X}$ is a continuous function, thus bounded on the closed interval generated by 0 and x. Therefor we find a c such that $e^{\tilde{x}} \leq c$ . We now choose an $m \in ℕ$ with $m \geq | x |$ and thus for all $n > m$ the following estimate holds:

0 \leq | \frac{e^{\tilde{x}}}{(n + 1)!} x^{n + 1} | \leq c \cdot \frac{| x |^{n + 1}}{(n + 1)!} = c \cdot \frac{| x |^{m + 1}}{m!} \cdot \underset{\leq 1}{\underset{︸}{\frac{| x |}{m + 1} \cdot \dots \cdot \frac{| x |}{n}}} \cdot \frac{1}{n + 1} \to 0

which in fact is the assertion due to the nesting theorem [5.5.8].

Moreover, [8.8.25] and [8.8.9] prove the identity

In [5.9.18] we introduced the exponential function $\exp : ℝ \to ℝ$ by $\exp (x) = \sum_{i = 0}^{\infty} \frac{x^{i}}{i!}$ and promised to show that $e^{X} = \exp$ in [8.8.1]. We start with a technical consideration (click for a much shorter proof using Taylor series).

Proposition: Let $x \in ℝ$ be arbitrary. Then each $n \in ℕ$ satisfies the following estimate:

- \frac{1}{2^{n}} \cdot e^{| 2 x |} \leq e^{x} - \sum_{i = 0}^{n} \frac{x^{i}}{i!} \leq \frac{1}{2^{n}} \cdot e^{| 2 x |}

[8.8.24]

Proof: There is nothing to show if $x = 0$ . The proof for $x \neq 0$ is by induction. Recall that the exponential function is strictly positive and increasing.

The base step in our induction ( $n = 0$ ) follows from the estimate

$- e^{| 2 x |} \leq - 1 \leq e^{x} - 1 \leq e^{x} \leq e^{| 2 x |}$

which is due to $e^{| 2 x |} \geq 1$ .
Now assume [8.8.24] is already valid for an arbitrary n. Considering the monotony of integration ([8.2.10]) now yields for

1. ► $x > 0$ , i.e. $| 2 x | = 2 x$ :

$- \frac{1}{2^{n}} \int_{0}^{x} e^{2 X} \leq \int_{0}^{x} e^{X} - \sum_{i = 0}^{n} \frac{X^{i}}{i!} \leq \frac{1}{2^{n}} \int_{0}^{x} e^{2 X}$ .

As $\frac{1}{2} \cdot e^{2 X}$ is a primitive of $e^{2 X}$ we get

$\begin{array}{l} - \frac{1}{2^{n + 1}} e^{2 x} \leq - \frac{1}{2^{n + 1}} e^{2 x} + \frac{1}{2^{n + 1}} & = - \frac{1}{2^{n + 1}} \cdot e^{2 X} |_{0}^{x} \\ \leq e^{X} - \sum_{i = 0}^{n} \frac{X^{i + 1}}{(i + 1)!} |_{0}^{x} \\ \leq \frac{1}{2^{n + 1}} \cdot e^{2 X} |_{0}^{x} = \frac{1}{2^{n + 1}} e^{2 x} - \frac{1}{2^{n + 1}} \leq \frac{1}{2^{n + 1}} e^{2 x}, \end{array}$

but this is the assertion as $2 x = | 2 x |$ and

$e^{X} - \sum_{i = 0}^{n} \frac{X^{i + 1}}{(i + 1)!} |_{0}^{x} = e^{x} - 1 - \sum_{i = 0}^{n} \frac{x^{i + 1}}{(i + 1)!} = e^{x} - \sum_{i = 0}^{n + 1} \frac{x^{i}}{i!}$ .

2. ► $x < 0$ , i.e. $| 2 x | = - 2 x$ :

$- \frac{1}{2^{n}} \int_{x}^{0} e^{- 2 X} \leq \int_{x}^{0} e^{X} - \sum_{i = 0}^{n} \frac{X^{i}}{i!} \leq \frac{1}{2^{n}} \int_{x}^{0} e^{- 2 X}$ .

In this case $- \frac{1}{2} \cdot e^{- 2 X}$ is a primitive of $e^{- 2 X}$ , so we have now

$\begin{array}{l} - \frac{1}{2^{n + 1}} e^{- 2 x} \leq \frac{1}{2^{n + 1}} - \frac{1}{2^{n + 1}} e^{- 2 x} & = \frac{1}{2^{n + 1}} \cdot e^{- 2 X} |_{x}^{0} \\ \leq e^{X} - \sum_{i = 0}^{n} \frac{X^{i + 1}}{(i + 1)!} |_{x}^{0} \\ \leq - \frac{1}{2^{n + 1}} \cdot e^{- 2 X} |_{x}^{0} = - \frac{1}{2^{n + 1}} + \frac{1}{2^{n + 1}} e^{- 2 x} \leq \frac{1}{2^{n + 1}} e^{- 2 x} . \end{array}$

With $- 2 x = | 2 x |$ and $e^{X} - \sum_{i = 0}^{n} \frac{X^{i + 1}}{(i + 1)!} |_{x}^{0} = - e^{x} + \sum_{i = 0}^{n + 1} \frac{x^{i}}{i!}$ we get

$- \frac{1}{2^{n + 1}} e^{| 2 x |} \leq - e^{x} + \sum_{i = 0}^{n + 1} \frac{x^{i}}{i!} \leq \frac{1}{2^{n + 1}} e^{| 2 x |}$

as a preliminary result which turns into the actual one when multiplied by $- 1$ .

[8.8.24] is a major step and we now have the identity of both exponential functions at hand:

Proposition: For all $x \in ℝ$ we have

e^{x} = \sum_{i = 0}^{\infty} \frac{x^{i}}{i!}

[8.8.25]

Proof: Due to [8.8.24] the following estimate holds for any fixed x:

0 \leq | e^{x} - \sum_{i = 0}^{n} \frac{x^{i}}{i!} | \leq \frac{1}{2^{n}} \cdot e^{| 2 x |} \to 0

which in fact is the assertion due to the nesting theorem [5.5.8].

Moreover, [8.8.25] and [8.8.9] prove the identity

\sum_{i = 0}^{\infty} \frac{x^{i}}{i!} = \lim (1 + \frac{x}{n})^{n}

[8.8.26]

which was already mentioned in 5.9 as a then alternative method to calculate $\exp (x)$ .

8.7. 8.9.